决策网络(Decision Network)

决策网络

• 决策网络：贝叶斯网络与最大期望(Expectimax)结合
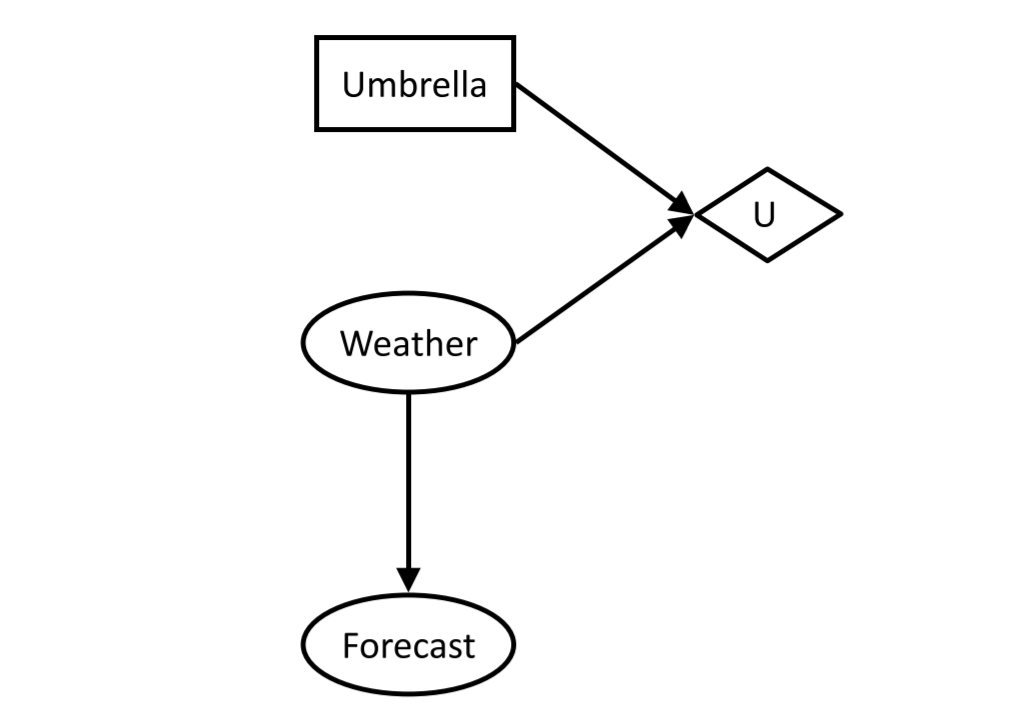
• 包含：
  • 概率节点(Chances nodes)(与贝叶斯网络中相同)
  • 动作节点(Actions)
    • 为矩形
    • 无父节点
    • 拥有完全的掌控权
  • 效用节点(Utility node)
    • 菱形
    • 取决于action和chance node
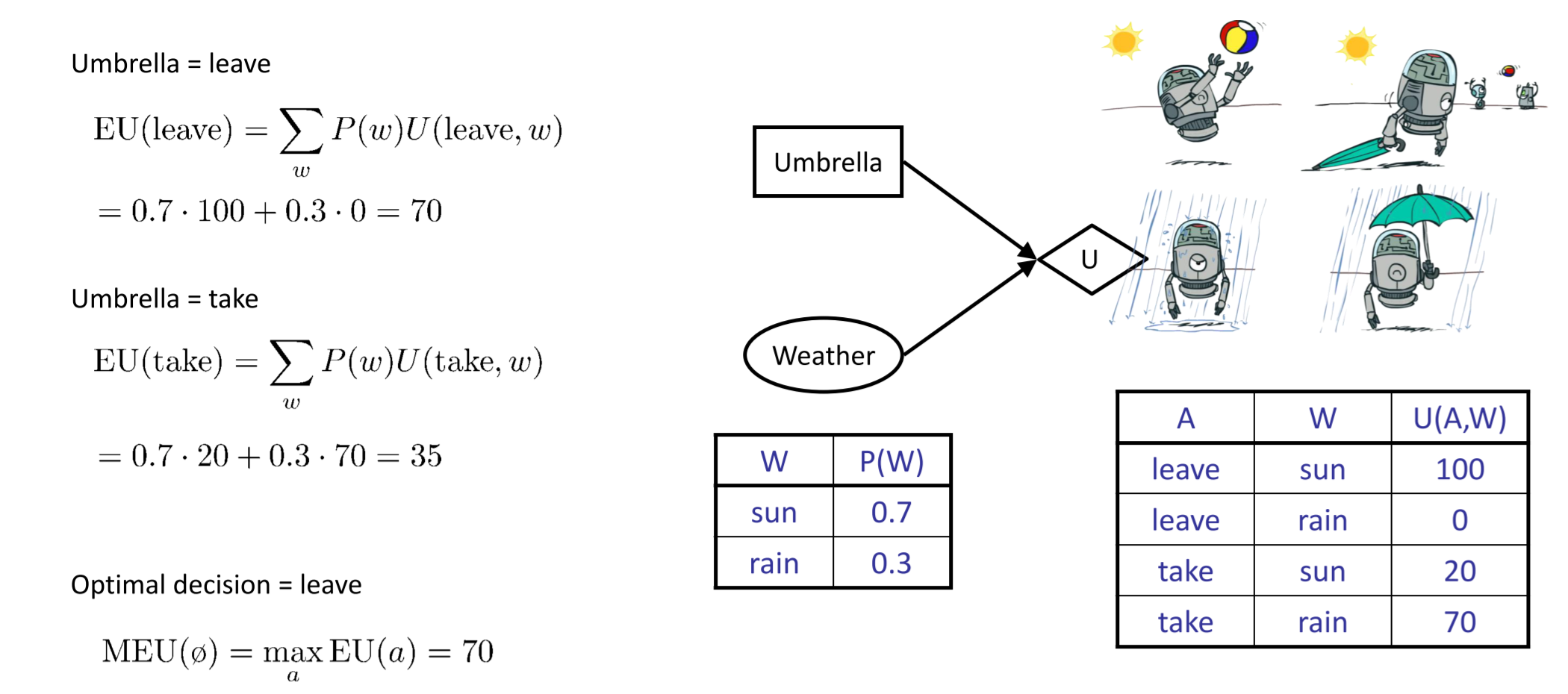
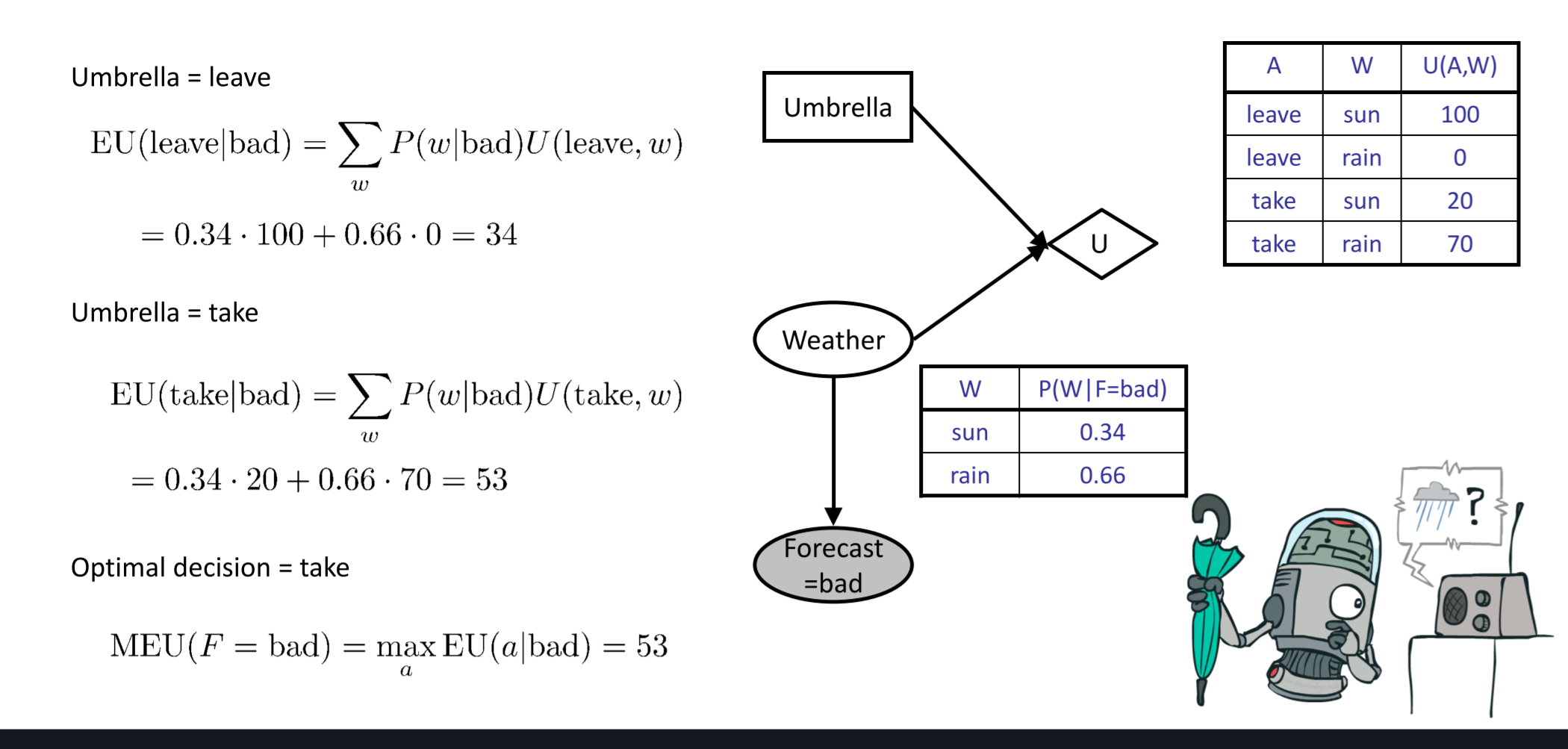
• MEU(Maximum Expected Utility)：在给定evidence的情况下，选择合适的action让期望效益(Expected Utility)最大化\(\(MEU(e)=\max_a\sum_sP(s|e)U(s,a)\)\)
• 目的：选择能够获得MEU的行动

过程

1. 实例化所有证据变量
2. 遍历动作节点的每一种可能方式
3. 针对所有的效用节点计算后验概率
4. 计算每一个行动下的期望效益
5. 选择最大期望效益

结果树(Outcome Trees)

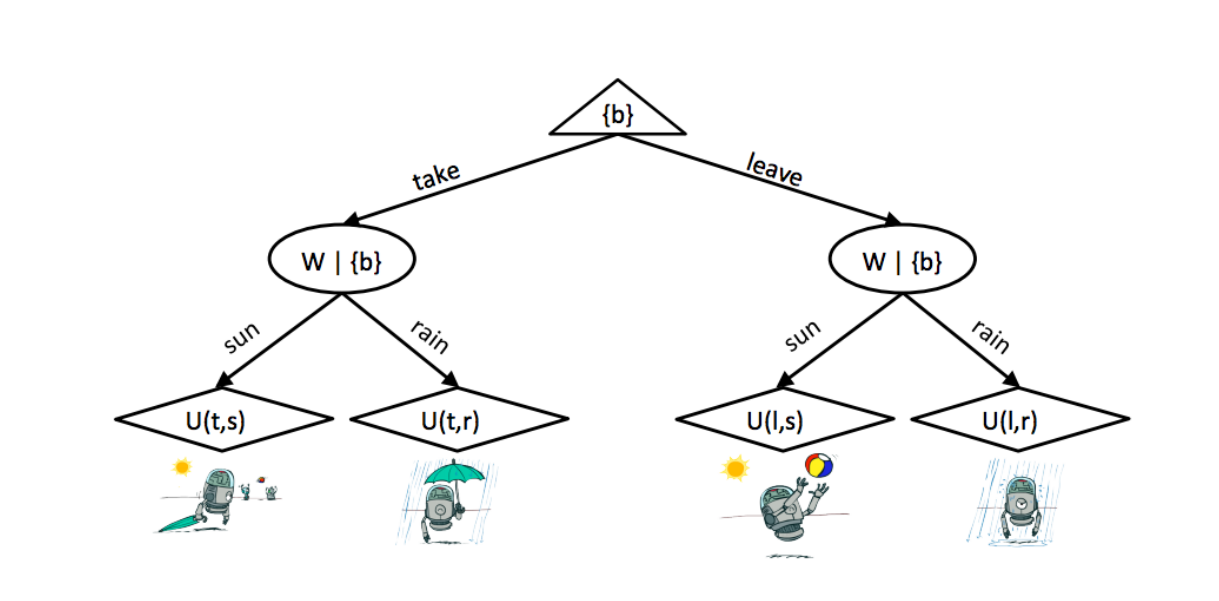- 顶部的节点是最大化节点，并且由我们控制

完美信息价值(VPI-The Value of Perfect Information)

• VPI：使用数值来衡量观测一个新的evidence的提升价值
• 一般公式（推导）
  1. 对于已有的evdience，可以得到如下公式：\(\(MEU(e)=\max_a\sum_sP(s|e)U(s,a)\)\)
  2. 如果继续对一个随机变量进行观察，再获得一个evidence，可以自然而然的得到如下公式：\(\(MEU(e,e^\prime)=\max_a\sum_sP(s|e,e^\prime)U(s,a)\)\)
  3. 但是我们无法确切知道接下来获得的evidence，因此使用\(E^\prime\)来代表\(e^\prime\)，那么使用加权平均的方式来表示MEU\(\(MEU(e,E^\prime)=\sum_{e^\prime}P(e^\prime|e)MEU(e,e^\prime)\)\)
  4. 可以提升的价值为：\(\(VPI(E^\prime|e)=MEU(e,e^\prime)-MEU(e)\)\)
• 案例：
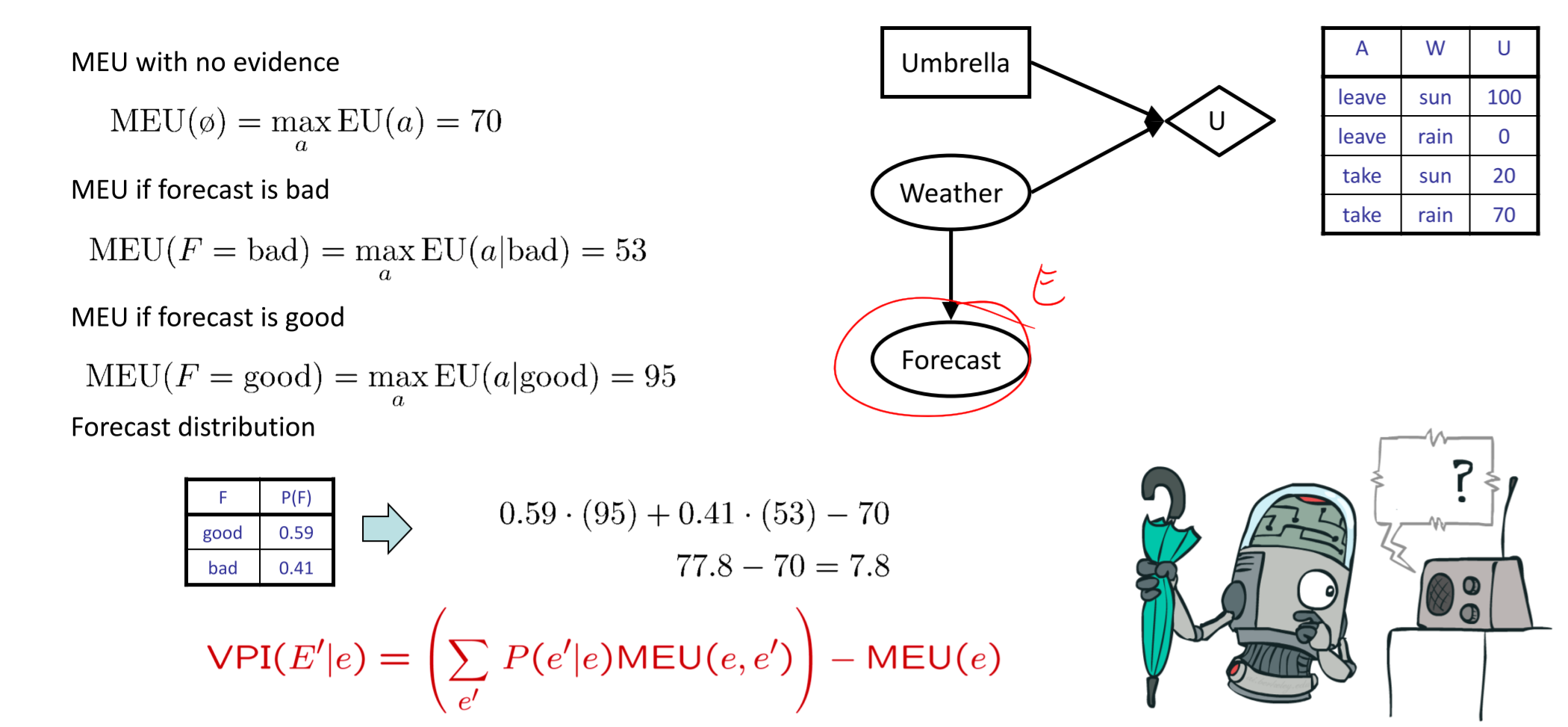
• 性质：
  • 非负性：\(\forall E^\prime, e:VPI(E^\prime |e) \geq 0\)
  • 不可加性：\(VPI(E_j,E_k|e)\ne VPI(E_j|e)+VPI(E_k|e)\)
  • 顺序独立性：\(VPI(E_j,E_k|e)= VPI(E_j|e)+VPI(E_k|e,E_j)=VPI(E_k|e)+VPI(E_j|e,E_k)\)