动态规划算法
- 动态规划的基本思想:将待求解的问题分为若干个子问题,先求解子问题,然后从这些子问题的解得到目标问题的解
- 两种基于动态规划的算法:
- 策略迭代
- 策略评估
- 使用贝尔曼期望方程来得到一个策略的状态价值函数
- 策略提升
- 策略评估
- 价值迭代
- 直接使用贝尔曼最优方程来进行动态规划,得到最终的最优状态价值函数
- 策略迭代
- 局限性:
- 通常只适用于有限马尔科夫决策过程(状态空间和动作空间是离散且有限的)
策略迭代算法
- 策略迭代算法是策略评估和策略提升不断循环交替,指导的到最优策略的过程
策略评估
- 贝尔曼期望方程:(\(V^\pi(s)=\sum_{a\in\mathcal{A}}\pi(a|s)(r(s,a)+\gamma\sum_{s^\prime\in\mathcal{S}}P(s^\prime|s,a)V^\pi(s^\prime))\)\)
- 当知道奖励函数和状态转移函数时,我们可以根据下一个状态的价值来计算当前状态的价值
- 把计算下一个可能状态的价值当成一个子问题,把计算当前状态的价值看成当前问题,则的状态转移方程:(\(V^{k+1}(s)=\sum_{a\in\mathcal{A}}\pi(a|s)(r(s,a)+\gamma\sum_{s^\prime\in\mathcal{S}}P(s^\prime|s,a)V^k(s^\prime))\)\)
计算值收敛时,可提前结束计算
- 把计算下一个可能状态的价值当成一个子问题,把计算当前状态的价值看成当前问题,则的状态转移方程:(\(V^{k+1}(s)=\sum_{a\in\mathcal{A}}\pi(a|s)(r(s,a)+\gamma\sum_{s^\prime\in\mathcal{S}}P(s^\prime|s,a)V^k(s^\prime))\)\)
- 当知道奖励函数和状态转移函数时,我们可以根据下一个状态的价值来计算当前状态的价值
策略提升
- 贪心的在每一个状态中选择动作价值最大的动作\(\(\pi^\prime(s)=arg\max_aQ^\pi(s,a)\)\)
策略迭代
- 迭代过程:
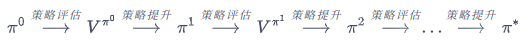
- 伪代码:
