时序差分算法

时序差分算法代码实现

[[时序差分算法#在线策略算法与离线策略算法|在线策略学习与离线策略学习]] - 在线策略学习： - 要求使用在当前策略下采样的到的样本进行学习 - 一旦策略被更新，当前的样本就被放弃了 - 类比在水龙头下直接使用自来水洗手 - 离线策略学习： - 使用经验回放池将之前采样得到的样本收集起来再次利用 - 类比使用脸盆接水后洗手

因此，离线学习能够更好的利用历史数据，并且具有更小的样本复杂度

时序差分

结合了蒙特卡洛和动态规划的思想
- 蒙特卡洛方法：可以从样本数据中学习，无需事先知道环境
- 动态规划：根据贝尔曼方程的思想，利用后续状态的价值估计来更新当前状态的价值
对于蒙特卡洛方法的优化：
- 蒙特卡洛方法：\(V(s_t)\leftarrow V(s_t)+\alpha [G_t-V(s_t)]\)
  - 我们可以将\(\alpha\)取值为一个常数，使更新方式不再像蒙特卡洛方法严格的取期望，称其为学习率
  - 在蒙特卡洛方法中，需要采集到整个序列才能进行更新
    - 而时序差分算法直接使用当前获得的奖励加上下一个状态的价值估计来作为在当前状态可以获得的回报，得到公式：(\(V\left(s_{t}\right) \leftarrow V\left(s_{t}\right)+\alpha\left[r_{t}+\gamma V\left(s_{t+1}\right)-V\left(s_{t}\right)\right]\)\)
      
      可以使用\(r_{t}+\gamma V\left(s_{t+1}\right)\)替代\(Q_t\)的原因：
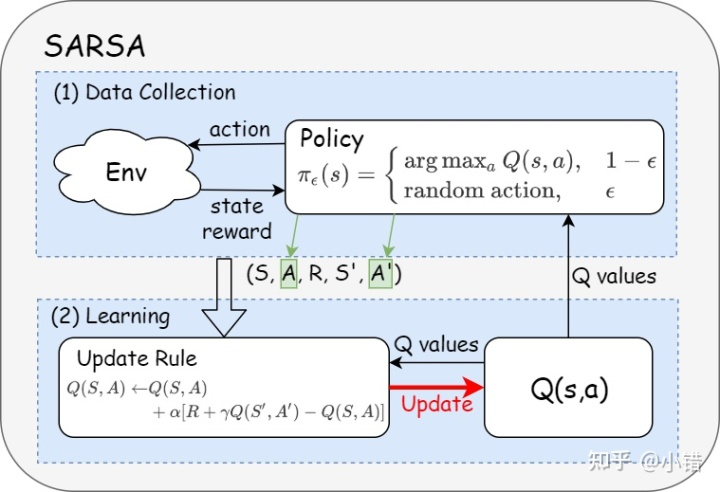
  Sarsa算法
  [!提出] - 在不知道奖励函数和状态转移函数的情况下如何进行策略提升？？？ - 答案：直接使用时序差分算法来进行估计状态价值函数\(Q(s,a)\)\(\(Q\left(s_{t}, a_{t}\right) \leftarrow Q\left(s_{t}, a_{t}\right)+\alpha\left[r_{t}+\gamma Q\left(s_{t+1}, a_{t+1}\right)-Q\left(s_{t}, a_{t}\right)\right]\)\) - 接下来使用贪婪算法来选取在某个状态下动作价值最大的动作：\(arg\max _{a} Q(s, a)\) - 完整的流程： - 使用贪婪算法根据动作价值选取动作来与环境进行交互 - 根据得到的数据用[[时序差分算法#时序差分|时序差分算法]]更新动作价值估计 - 两个问题与对应的解决： - 如果要使用时序差分算法来准确估计策略的状态价值函数，我们需要用极大量的样本来进行更新 - 直接使用一些样本来评估策略 - 策略提升可以在策略评估未完全完成时候进行 - 如果一直使用贪婪策略来选取动作，可能导致有些动作一直未被选取 - 使用\(\epsilon\)贪婪算法由此得到Sarsa算法 - Sarsa算法的具体流程： - 流程图： - 代码：
```
state = env.reset()
action = agent.take_action(state)
done = False
while not done:
    next_state, reward, done = env.step(action)
    next_action = agent.take_action(next_state)
    episode_return += reward
    agent.update(state, action, reward, next_state, next_action)
    state = next_state
    action = next_action
```

多步Sarsa算法

多步时序差分：使用n步的奖励，然后使用之后状状态的价值估计
与单步Sarsa在公式上的变化：\(\(\begin{aligned}Q\left(s_{t}, a_{t}\right) \leftarrow Q\left(s_{t}, a_{t}\right)+\alpha\left[r_{t}+\gamma Q\left(s_{t+1}, a_{t+1}\right)-Q\left(s_{t}, a_{t}\right)\right]\\\Downarrow\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\Q\left(s_{t}, a_{t}\right) \leftarrow Q\left(s_{t}, a_{t}\right)+\alpha\left[r_{t}+\gamma r_{t+1}+\cdots+\gamma^{n} Q\left(s_{t+n}, a_{t+n}\right)-Q\left(s_{t}, a_{t}\right)\right]\end{aligned}\)\)

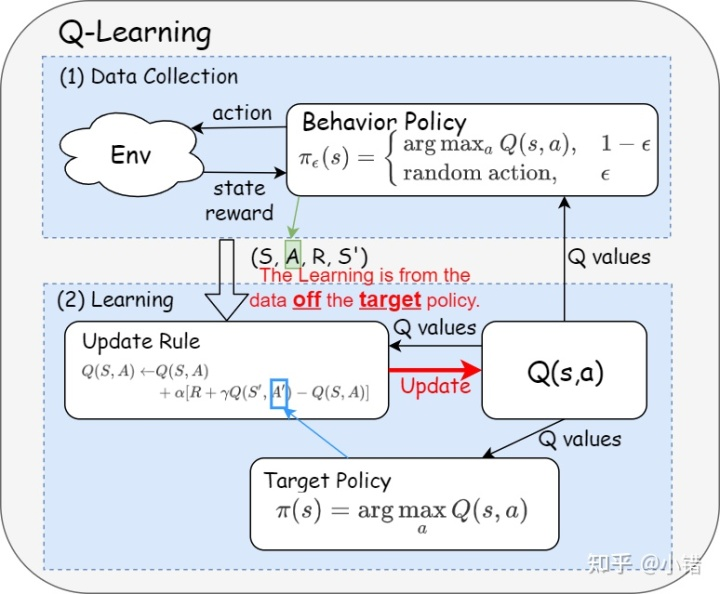
Q-Learning算法

与Sarsa的区别：时序差分更新的方式：\(\(Q\left(s_{t}, a_{t}\right) \leftarrow Q\left(s_{t}, a_{t}\right)+\alpha\left[R_{t}+\gamma \max _{a} Q\left(s_{t+1}, a\right)-Q\left(s_{t}, a_{t}\right)\right]\)\)
具体流程：

在线策略算法与离线策略算法

两种策略的介绍：
- 行为策略：采集数据的策略
  - 专门负责学习数据的策略
  - 具有一定的随机性
  - 有一定的概率选出潜在的最优动作
- 目标策略：用采集来的数据所被更新的策略
  - 借助行为策略收集到的样本以及策略提升方法提升自身性能，并最终成为最优策略

离线策略算法

离线策略算法：the learning is from the data off the target policy
- 数据来源于一个单独的用于探索的策略
- 行为策略与目标策略不是同一个策略

在线策略算法

在线策略算法：the target and the behavior polices are the same
- 在在线策略算法中，只有一种策略，既是目标策略又是行为策略
- 行为策略与目标策略不是一个策略