概率(Probabilistic)

在人工智能中，常常需要基于各种各样的不确定时间进行建模

随机变量(Random Variables)

• 不确定的变量
• 一般来说，使用大写字母来指明随机变量

概率分布(probability Distributions)

联合概率分布(Joint Distributions)

• 遵守：
  • \(P(x_1,x_2,...,x_n)\geq 0\)
  • \(\sum P(x_1,x_2,...,x_n)=1\)
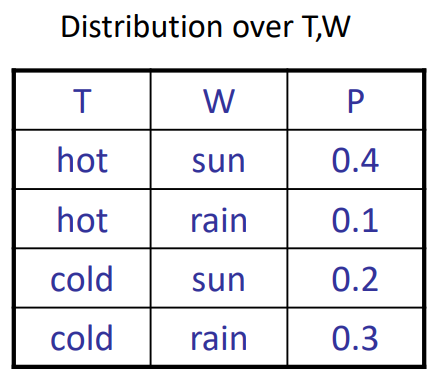
• 事件(Event)：结果的一个集合<-\(P(E)=\sum_{({x_1,x_2,...,x_n}\in E)}P(x_1,x_2,...,x_n)\)
• 通过联合概率分布，我们可以计算出任意一个事件发生的概率

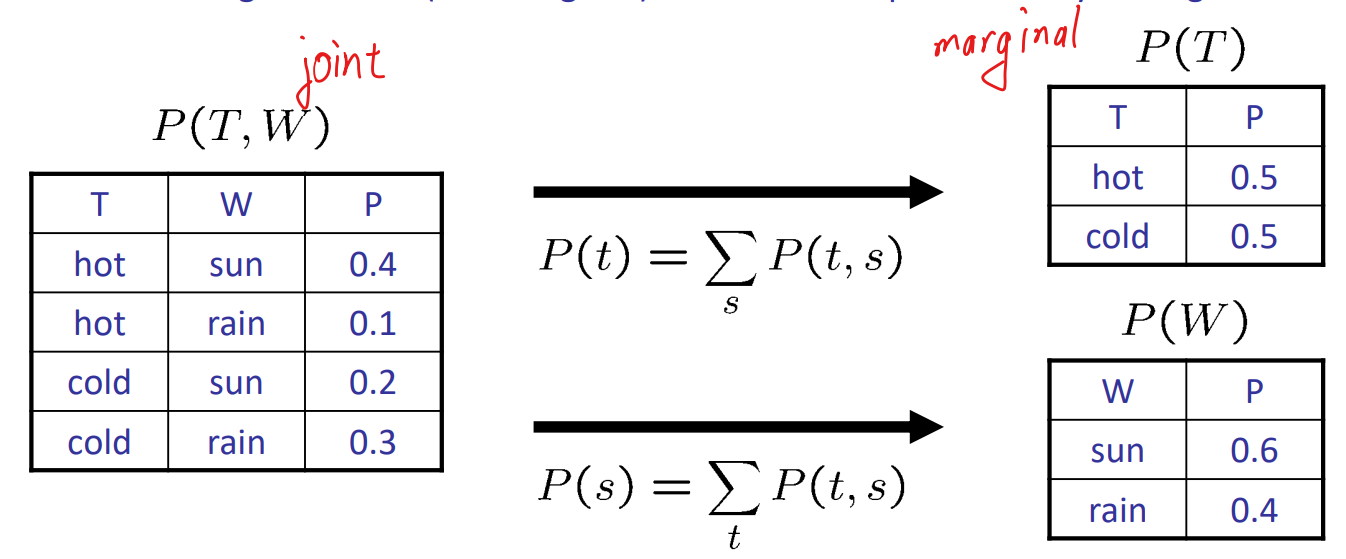
边缘分布(Marginal Distributions)

• 边缘分布是剔除其他变量后的子分布

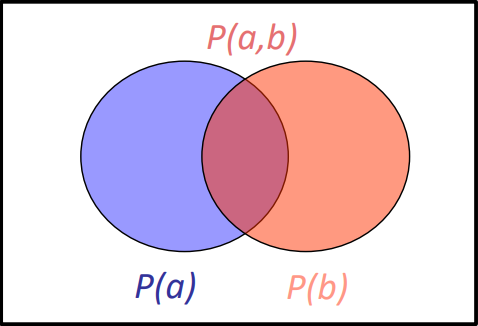
条件概率分布

\(\(P(a|b)=\frac{P(a,b)}{P(b)}\)\)

归一化(Normalize)

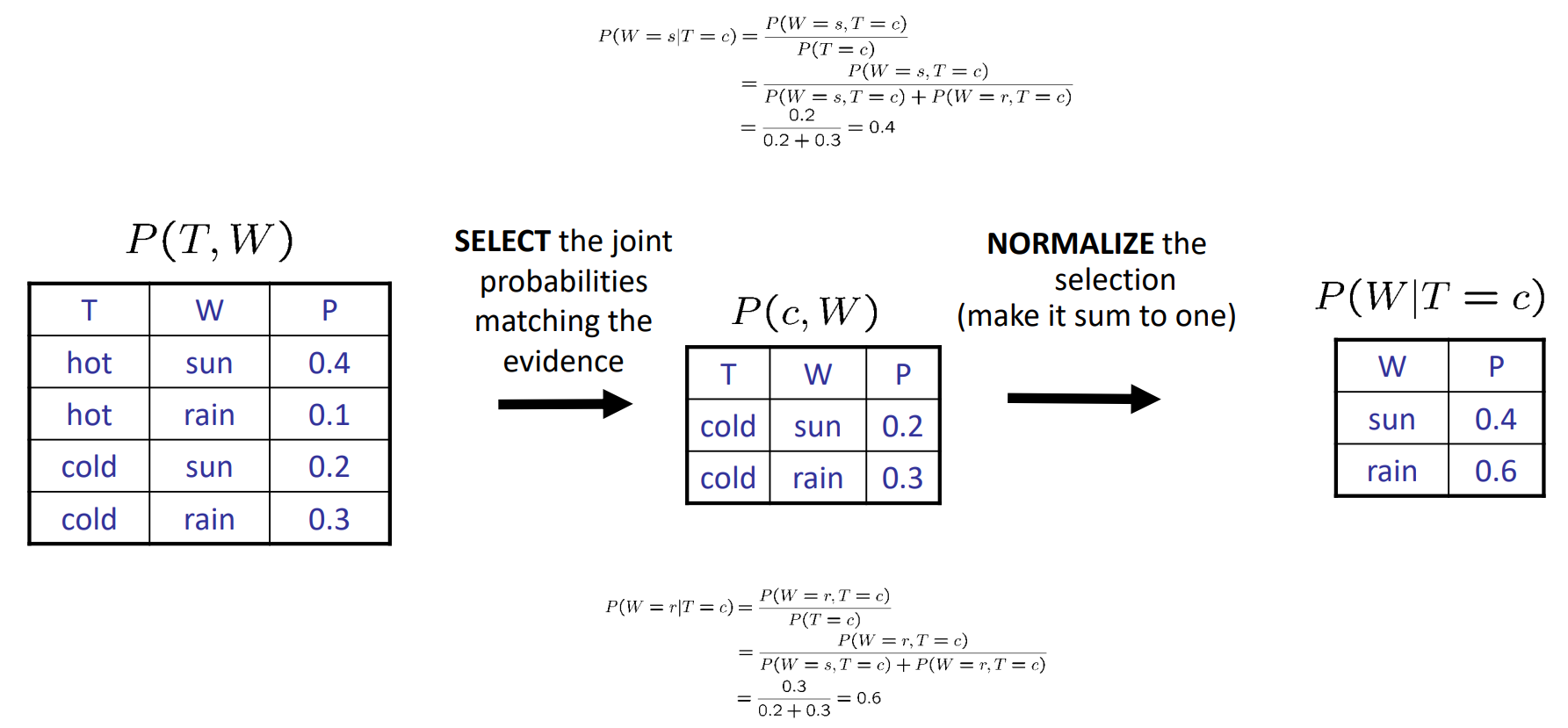
概率推理(Probabilistic Inference)

• 从已知的概率中推算出想要的概率

枚举推理

• 为了得到目标概率，我们需要解决：
  • 查询变量(Query variables \(Q_i\))：未知，并且尝试计算概率的变量
  • 证据变量(Evidence variables \(e_i\))：已知，并且用于计算目标概率（被观测，已确定）
  • 隐藏变量(Hidden variables)：其他无用的变量
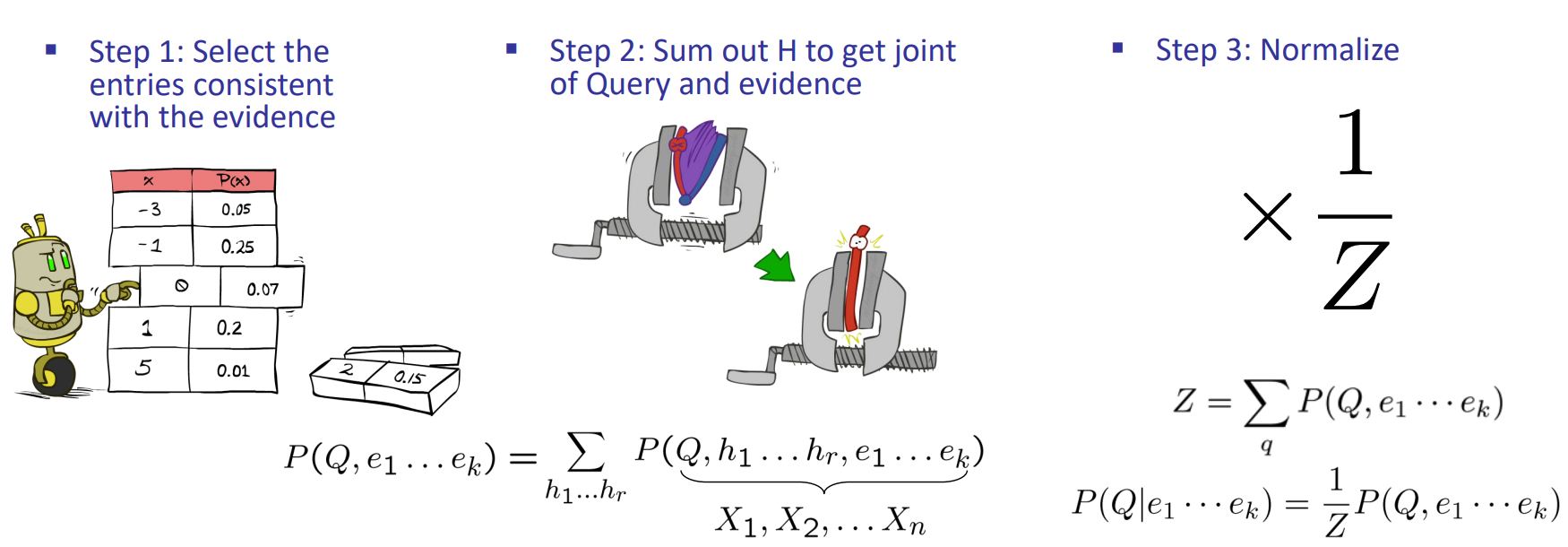
• 步骤：
  • Select the entries consistent with the evidence
  • Sum out H to get joint of Query and evidence
  • Normalize