贝叶斯网络(Bayesian Network)
独立(Indenpendence)
- 两者(随机变量)之间互不影响 \(\(\forall x,y:P(x,y)=P(x)P(y)\Longrightarrow X \perp Y\)\) \(\(\forall x,y:P(x|y)=P(x)\Longrightarrow x \perp y\)\) \(\(\forall x,y:P(y|x)=P(y)\Longrightarrow x \perp y\)\)
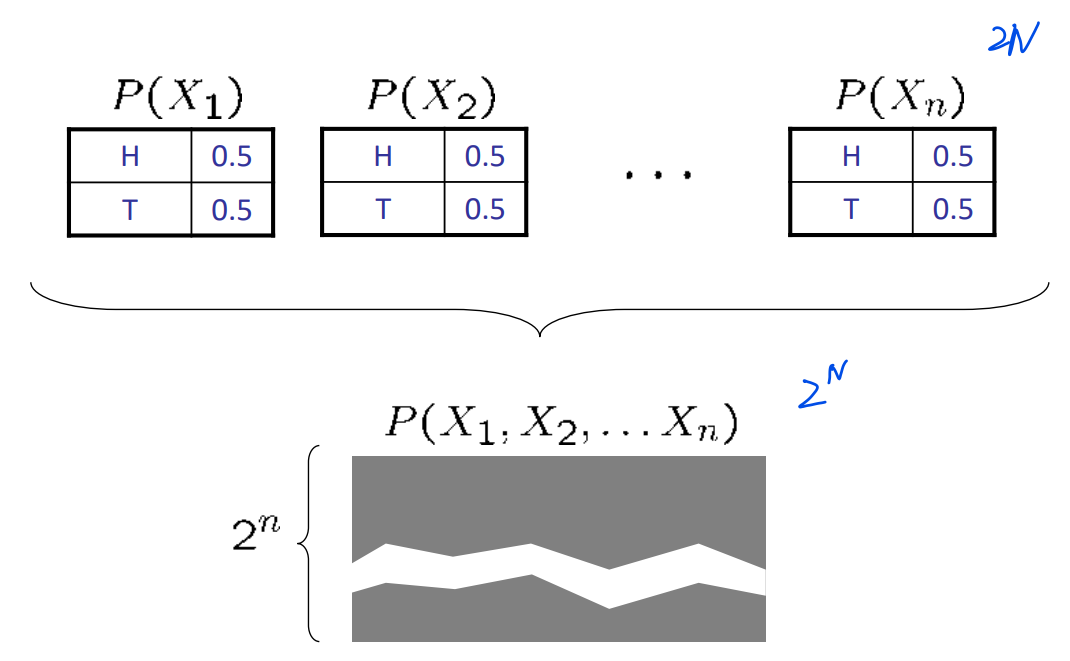
- 可以将投掷硬币的情况写成如下,极大减少了数据量
条件独立(Conditional Independence)
- 对于未知的环境,条件独立是我们最基础的和最直接的了解形式
- \(X\)与\(Y|Z\)条件独立:\(X \perp \!\!\! \perp Y|Z\)
- 当且仅当Z发生时,知道X发生是否无助于知道Y发生与否 \(\(\forall x,y,z:P(x,y|z)=P(x|z)P(y|z) \Longrightarrow X\perp \!\!\! \perp Y|Z\)\) \(\(\forall x,y,z:P(x|z,y)=P(x|z)\)\)
- 链式法则:\(P(X_1,X_2,...,X_n)=P(X_1)P(X_2|X_1)P(X_3|X_1,X_2)...\)

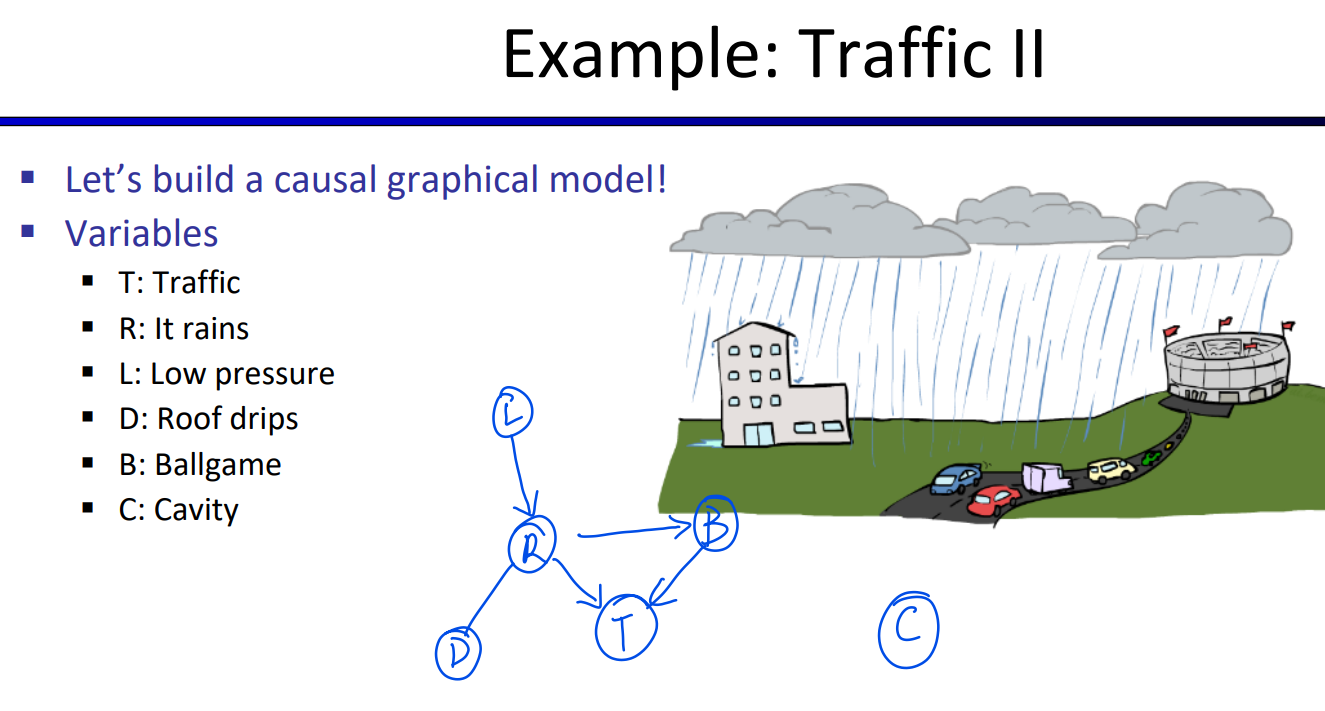
- \(P(Traffic, Rain, Umbrella)\)
- 链式法则:\(P(Traffic, Rain, Umbrella) = P(Rain)P(Traffic|Rain)P(Umbrella|Rain, Traffic)\)
- 由于\(Traffic\perp \!\!\! \perp Umbrella|Rain\):\(P(Traffic, Rain, Umbrella) = P(rain)P(Traffic|Rain)P(Umbrella|Rain)\)
贝叶斯网络:表示(Bayesian Network:Representation)
联合分布的缺点
- 在随机变量较多的时候,数据量大
- 难以一次从经验上学习关于多个变量的任何东西
贝叶斯网络
- 贝叶斯网络:使用简单的方式(有向无环图(DAG))表达复杂的联合分布概率模型
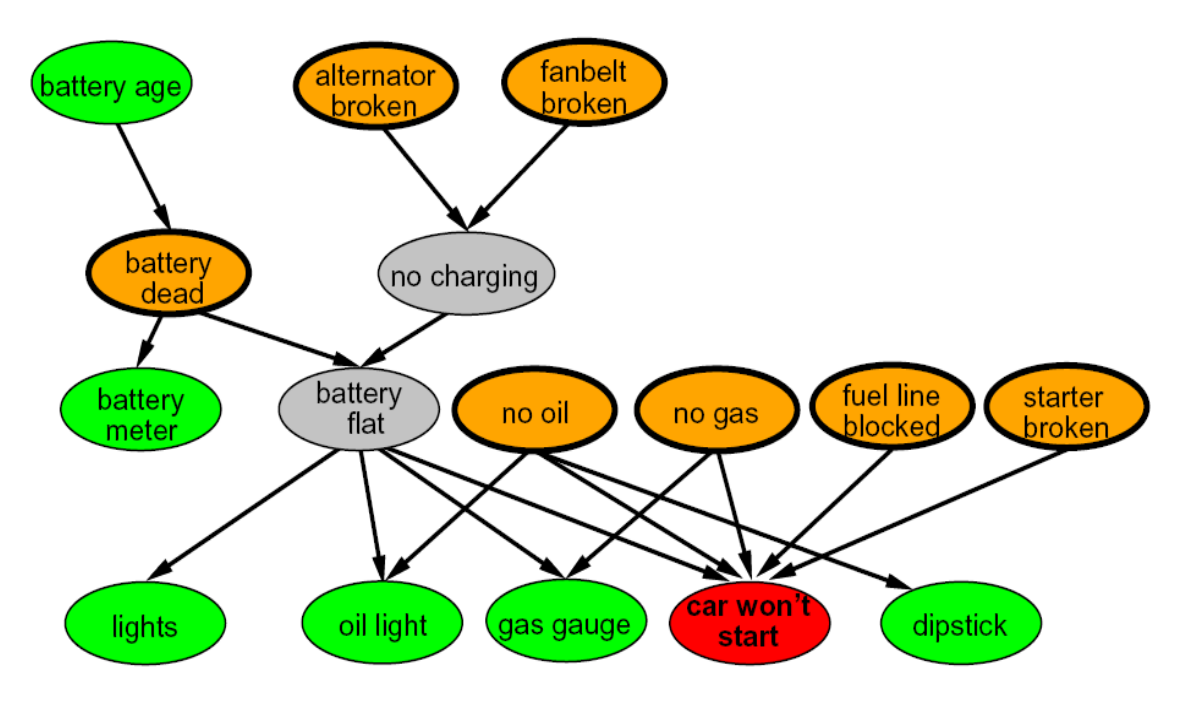
- 图
- 结点:随机变量
- 每个节点具有一个条件概率分布
- Each node is conditionally independent of all its ancestor nodes in the graph, given all of its parents
- 让\(A_1,A_2,...,A_N\)为X的双亲以存储\(P(X|A_1,A_2,...,A_N)\)
- 弧:因果关系或非条件独立
- 结点:随机变量
- 贝叶斯网络与条件独立:(\(P(x_1,x_2,...,x_n)=\prod^{n}_{i=1}P(x_i|parents(X_i))\)\)
- 案例:\(P(+cavity,+catch,-toothache)=P(+cavity)·P(+catch|+cavity)·P(-toochache|+cavity)\)
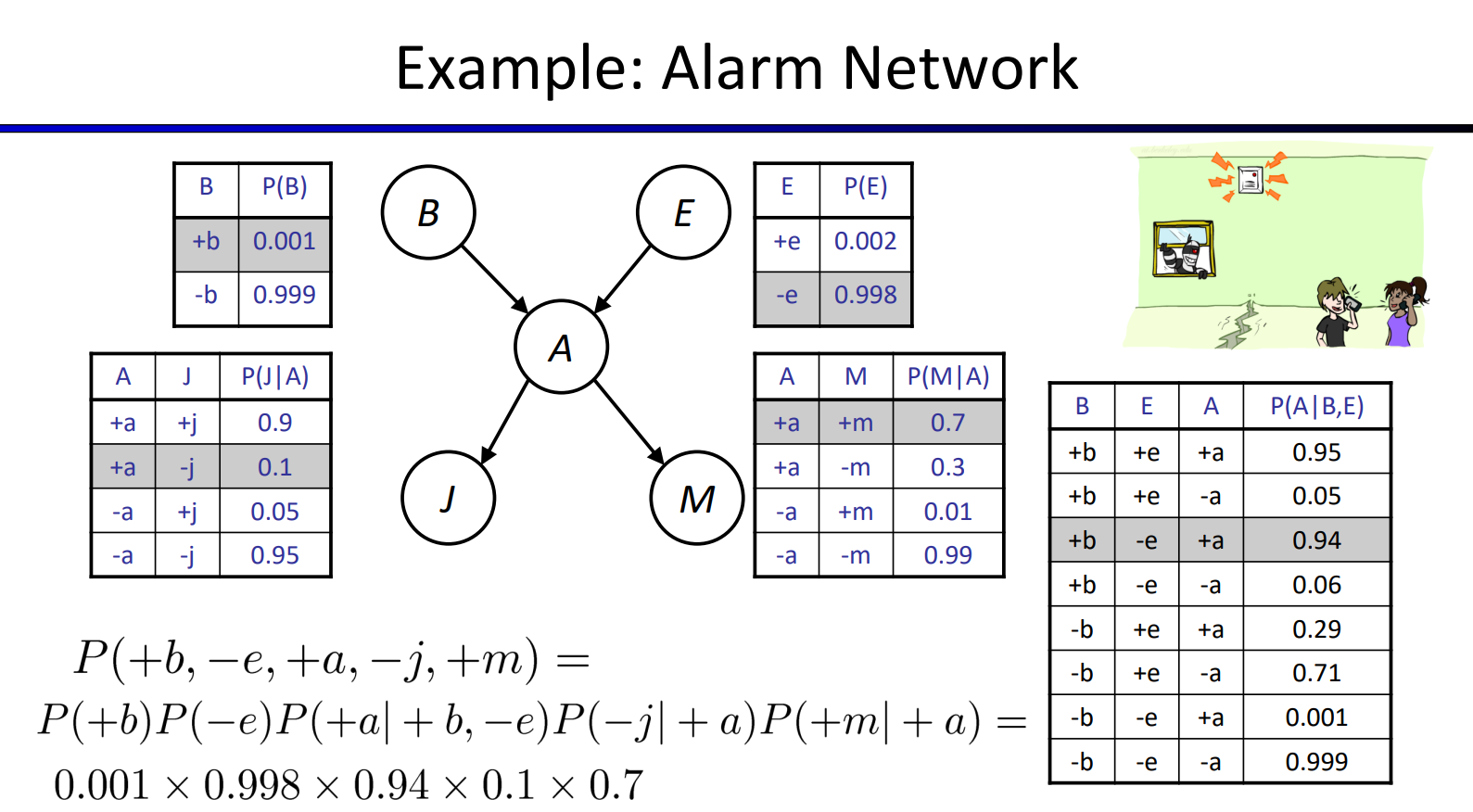
- 案例:\(P(+cavity,+catch,-toothache)=P(+cavity)·P(+catch|+cavity)·P(-toochache|+cavity)\)
- 大小
- 联合分布概率模型:\(2^n\)
- n个节点且每个节点最多k个双亲的贝叶斯网络:\(n*2^{k+1}\)
贝叶斯网络:条件独立(Conditional Indenpendence)
- D-separation
- 研究三元组的独立性
- 通过多个三元组研究复杂的情况
- 分类:
- Causal Chains
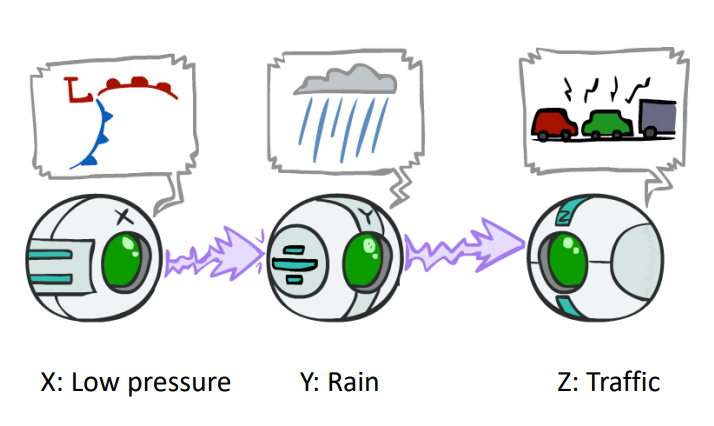
- \(X\perp\!\!\!\perp Y|Z\)
- Common Cause
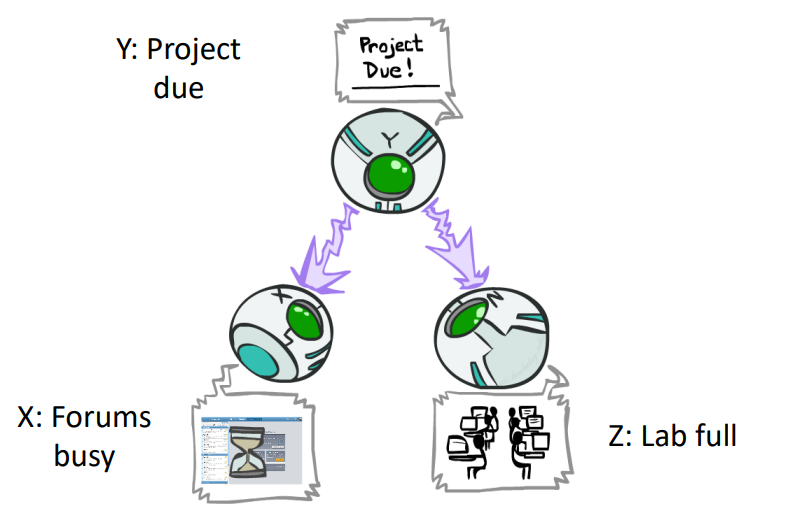
- \(X\perp\!\!\!\perp Y|Z\)
- Common Effect
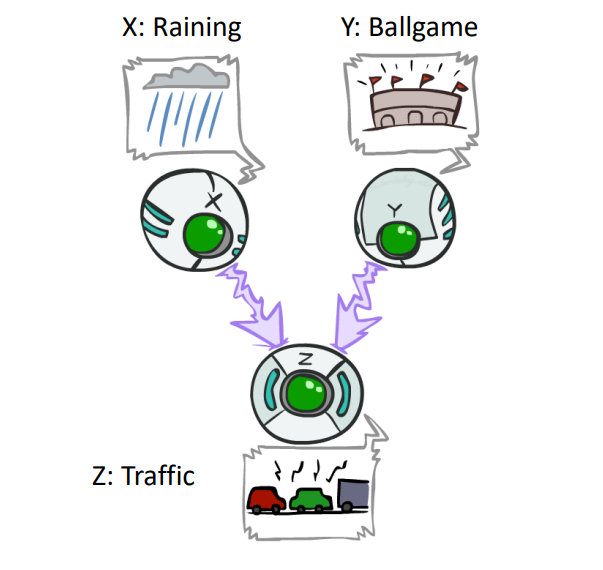
- \(X\perp\!\!\!\!\!\!\!\!\not\perp Y|Z,X\perp Y\)
- Causal Chains
- Active/Inactive Paths
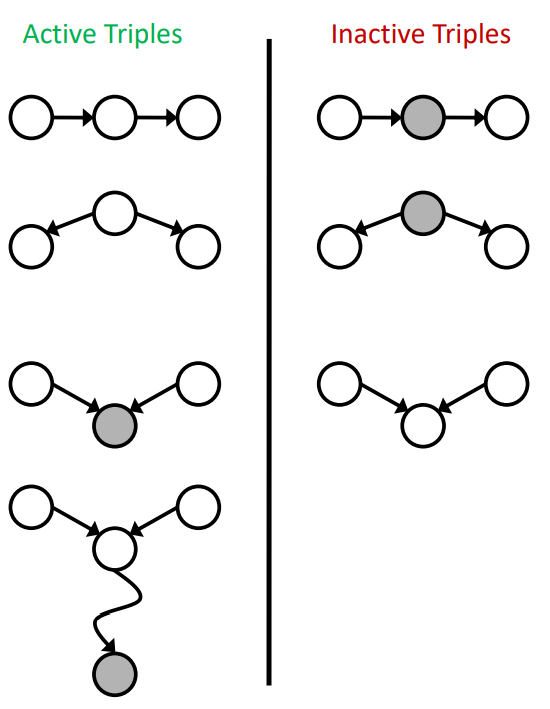 ^84522f
^84522f - 可达性
- 方法:将证据节点涂上阴影,再查看两个节点之间的路径
- 判断:如果两个节点之间的所有三元组均为Inactive Paths,则两个节点代表的随机变量条件独立
- 示例:

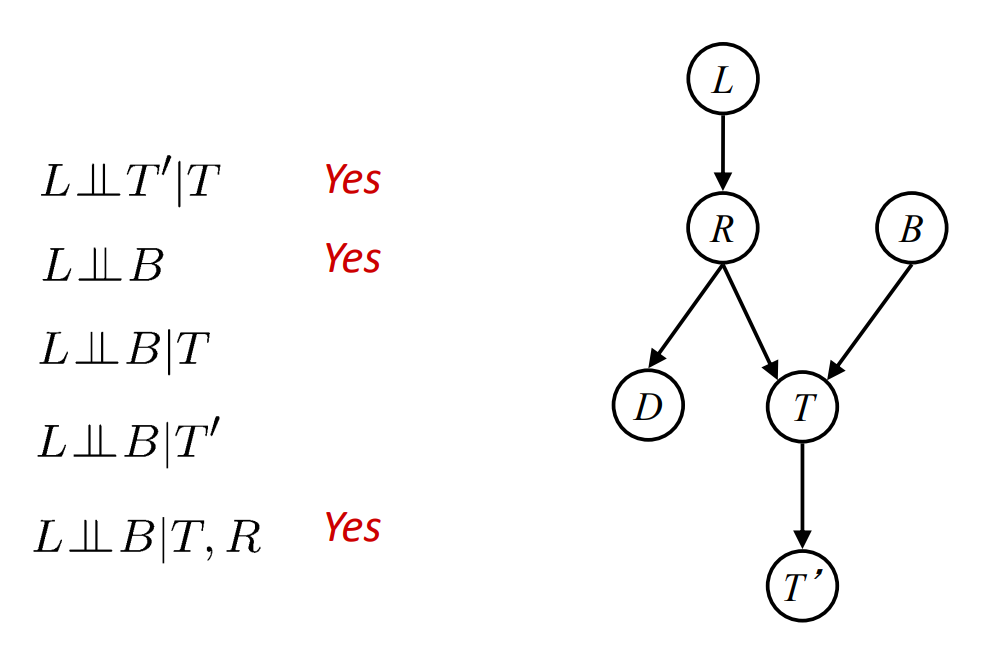
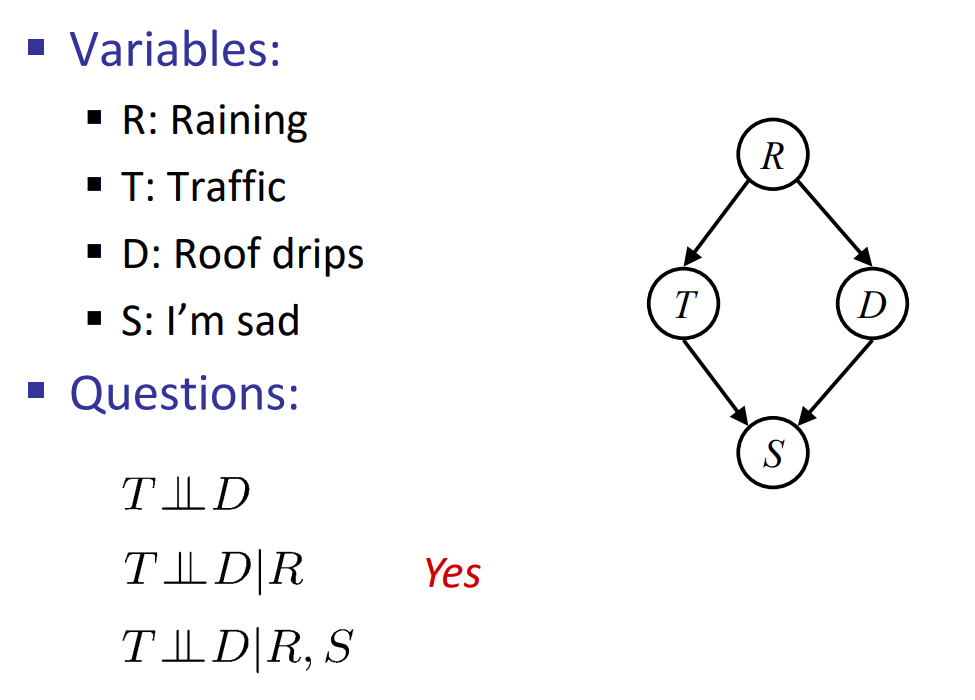
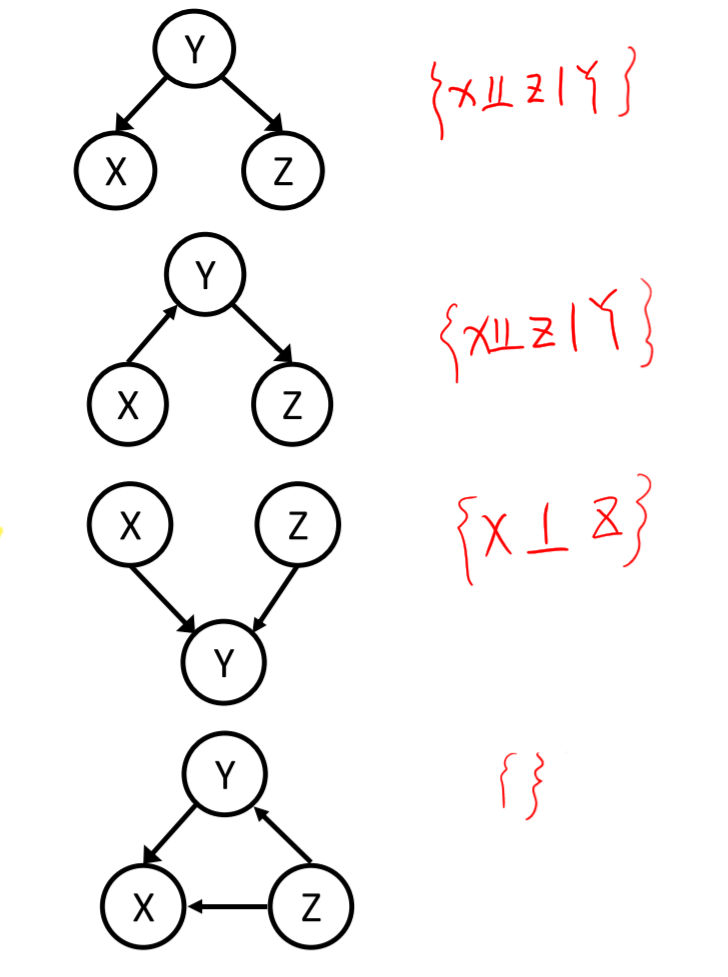
- 不同的贝叶斯网络可能指向相同的独立性:
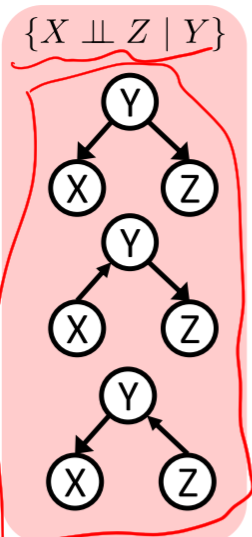
- 一个贝叶斯网络可能不存在任何独立性:

贝叶斯网络:推导(Probabilistic Inference)
- Inference:从一个联合分布概率模型中计算其他想要的概率
枚举推理(Inference by Enumeration)
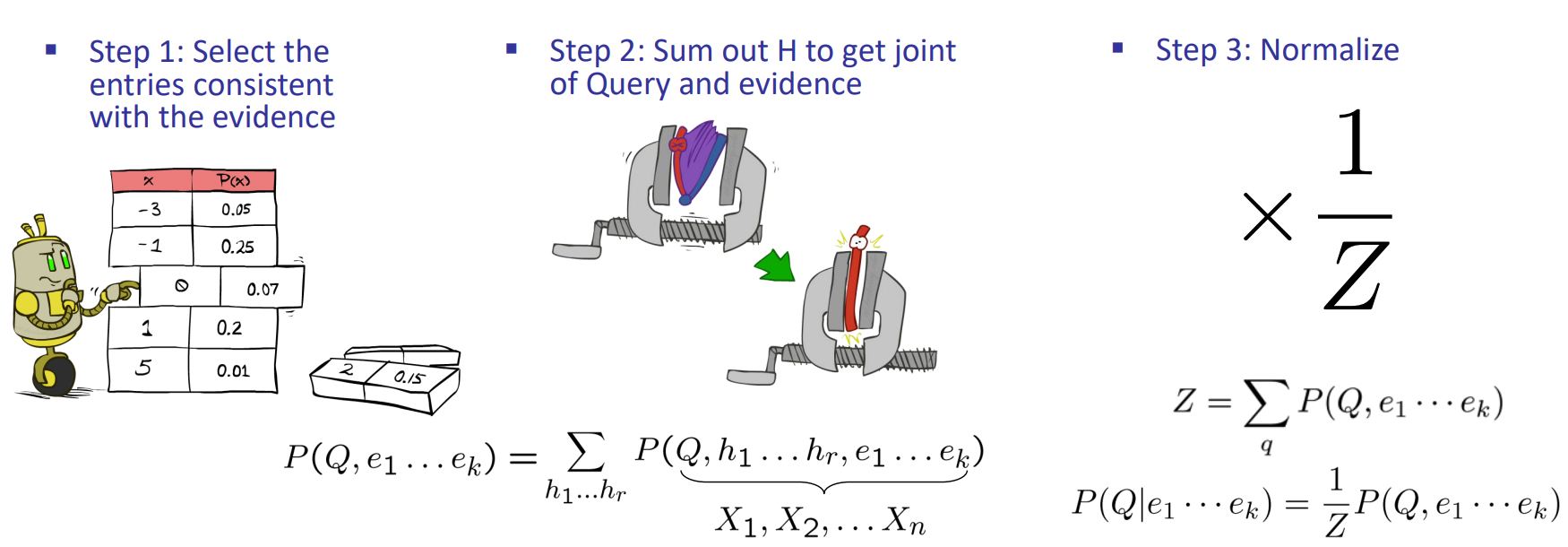
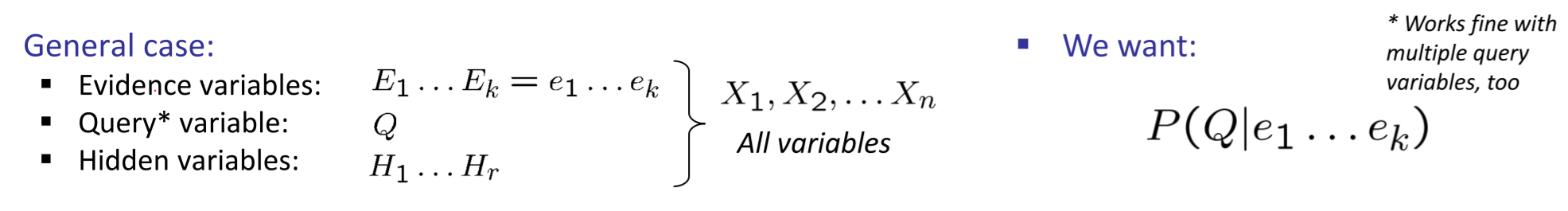 - 步骤:
- Select the entries consistent with the evidence
- Sum out H to get joint of Query and evidence(Marginalize)
- Normalize
- 步骤:
- Select the entries consistent with the evidence
- Sum out H to get joint of Query and evidence(Marginalize)
- Normalize
 - 案例:
- 案例:
变量剔除(Variable Elimination)
- 在枚举推理中,在去除其他隐变量之前,加入了完整的联合分布概率,导致枚举推理运行效率低
- 变量剔除:交叉加入并且即时进行边缘化操作
因子(Factors)
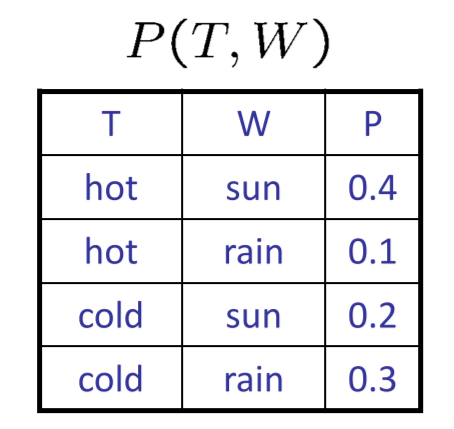
- Joint Distribution:\(P(X,Y)\)
- 和为1
- 包含了x,y的所有条目
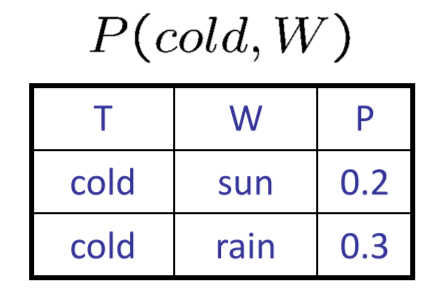
- Selected Joint:\(P(x,Y)\)
- 联合概率分布的一部分
- 包含固定的x,所有的y的条目
- 和为\(P(x)\)
大写字母的数量=表的维度数
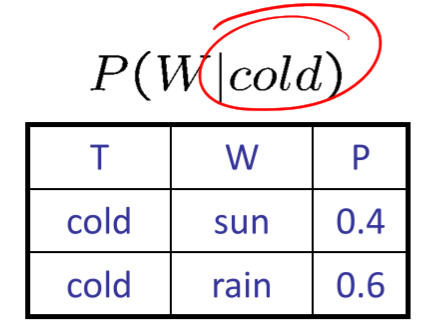
- Single Conditional:\(P(Y|x)\)
- \(x\)条件下的所有\(P(y|x)\)
- 和为1
- Family of conditionals:\(P(Y|X)\)
- 所有的\(P(y|x)\)条目
- 和为\(|X|\)

- Specified Family:\(P(y|X)\)
- 固定\(y\)的所有\(P(y|x)\)条目

- 固定\(y\)的所有\(P(y|x)\)条目
两种方案对比
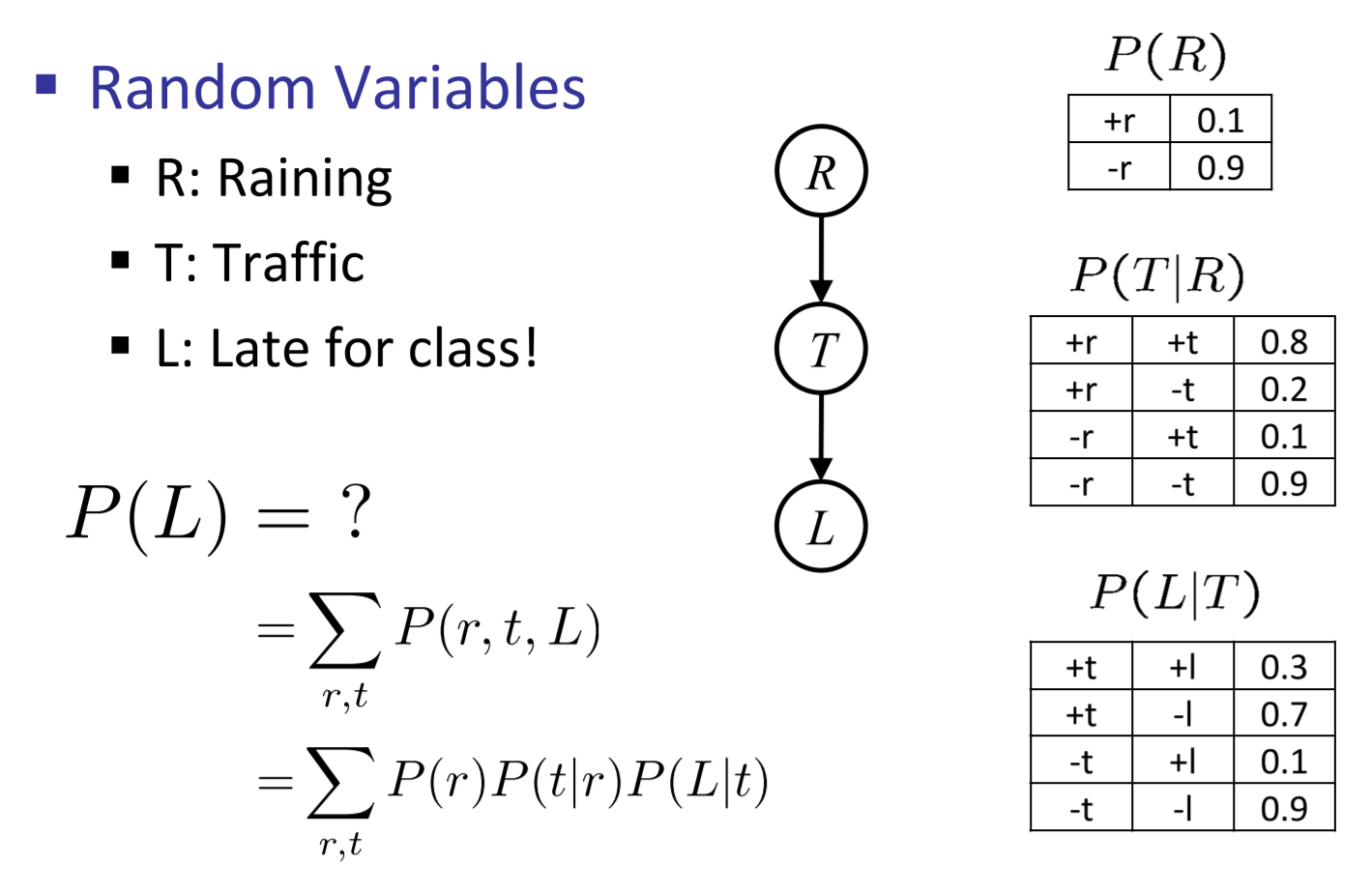
Inference by Enumeration
- Join all factors
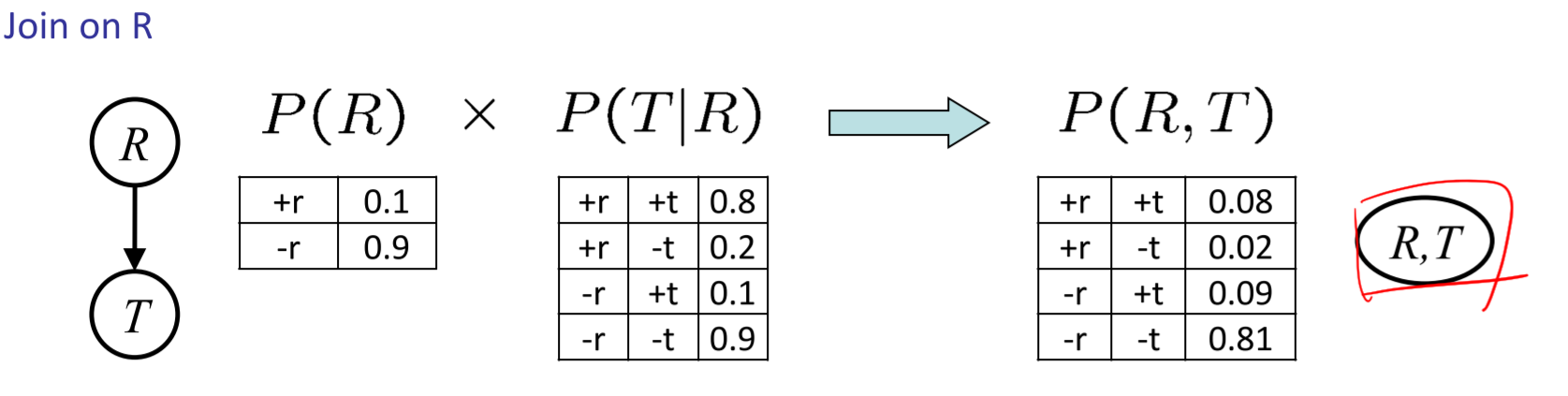
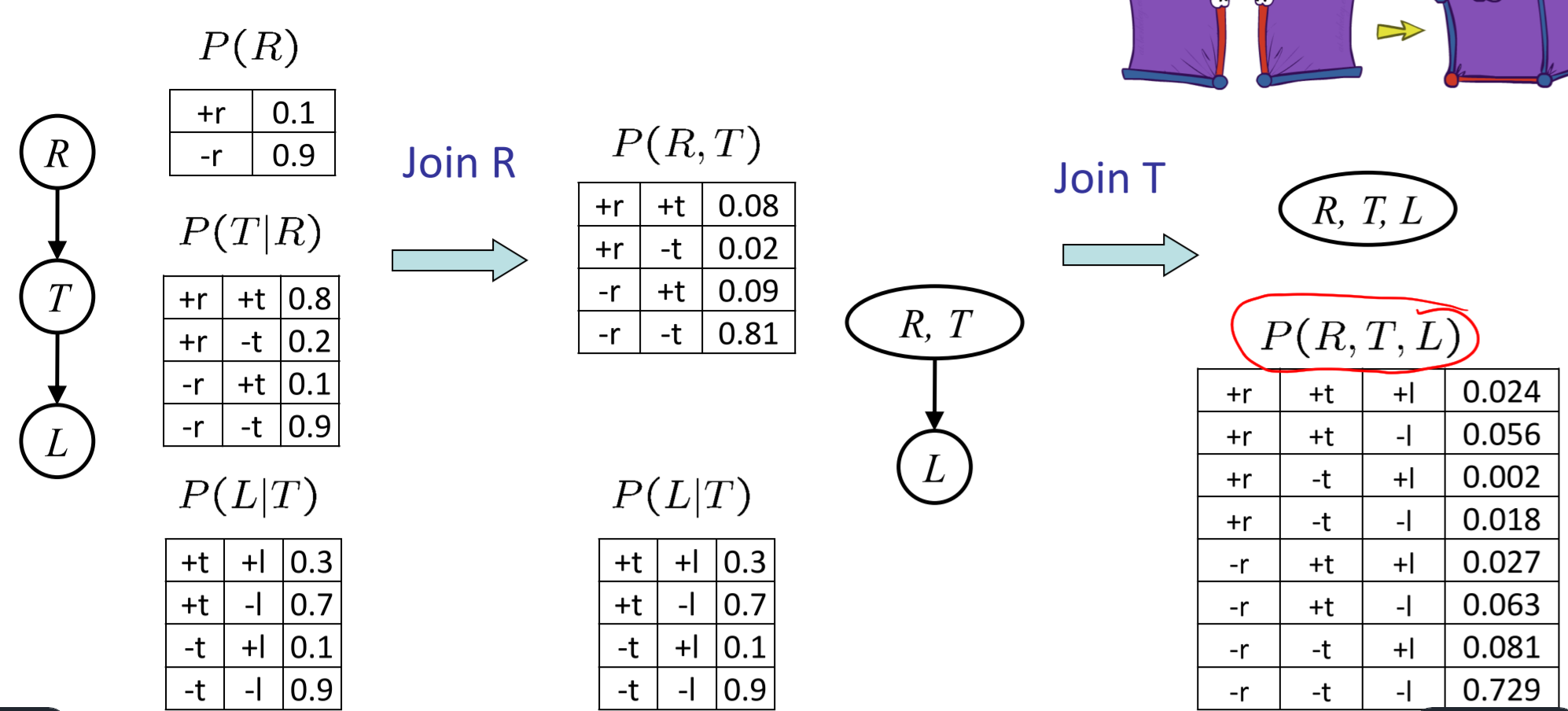
\(\(\forall r,t:P(r,t)=P(r)·P(t|r)\)\)
- Eliminate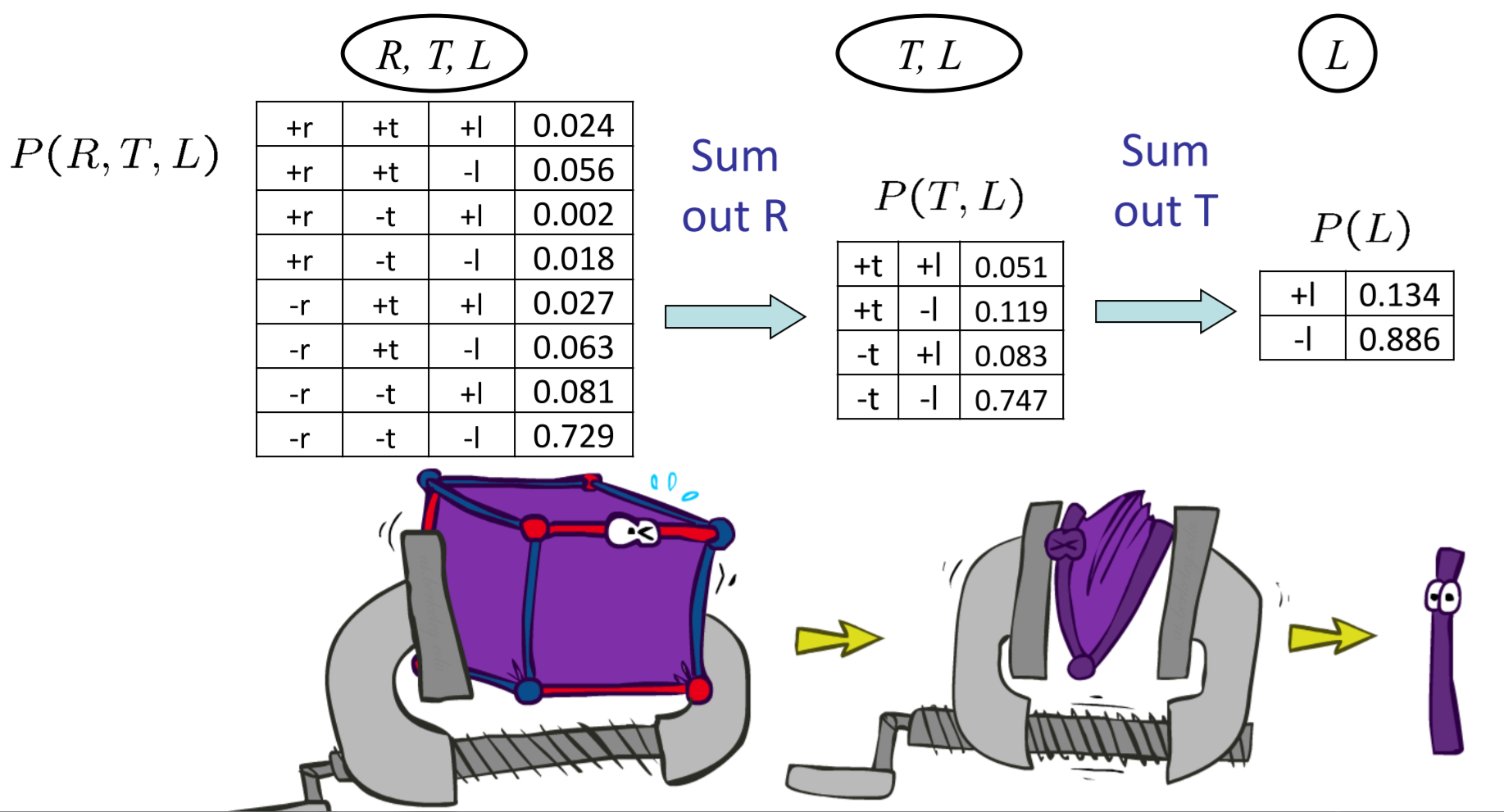
Variable Elimination
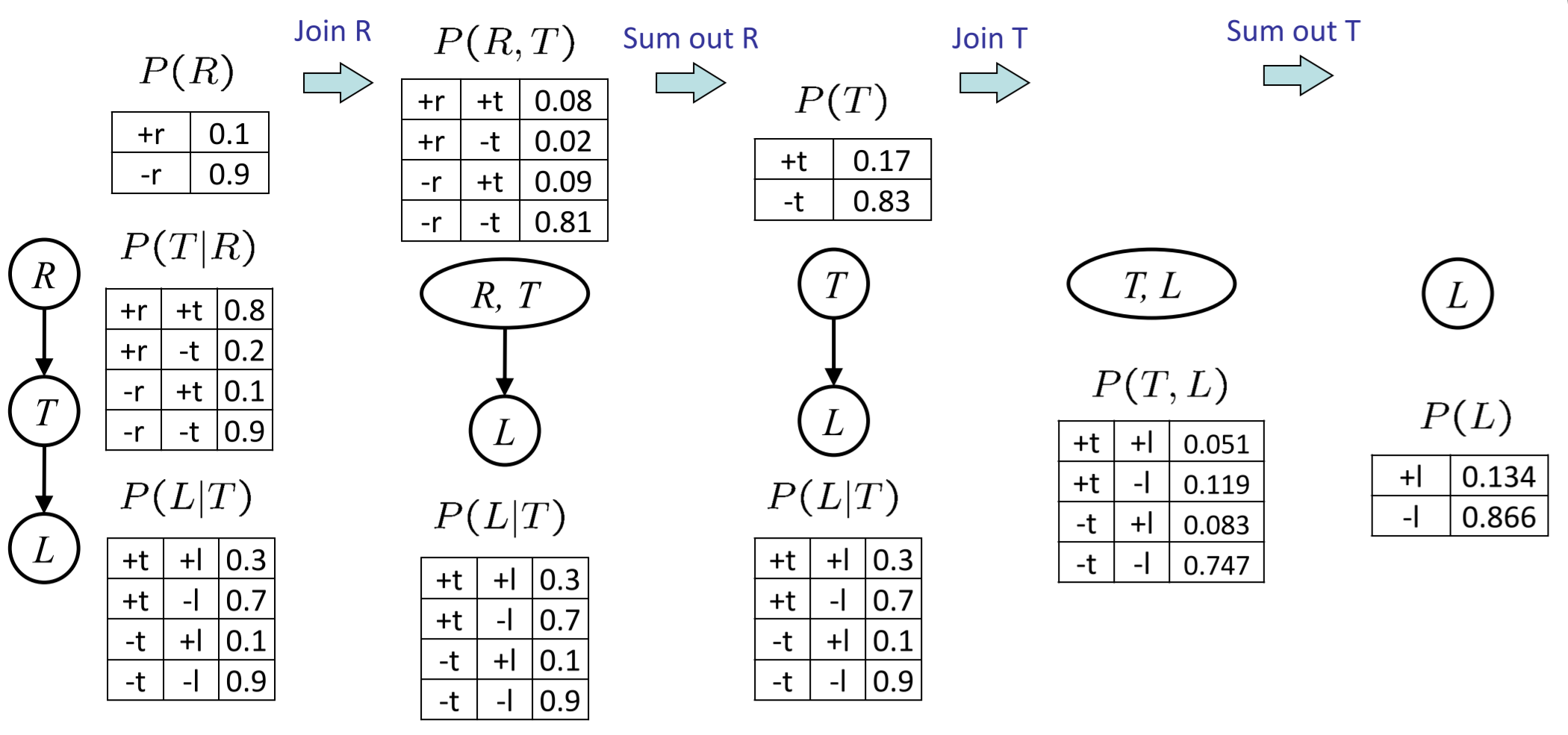 - 一般情况下,变量剔除的顺序会极大影响计算的复杂度
- 案例:
- 一般情况下,变量剔除的顺序会极大影响计算的复杂度
- 案例: 1. 法一:
1. 法一: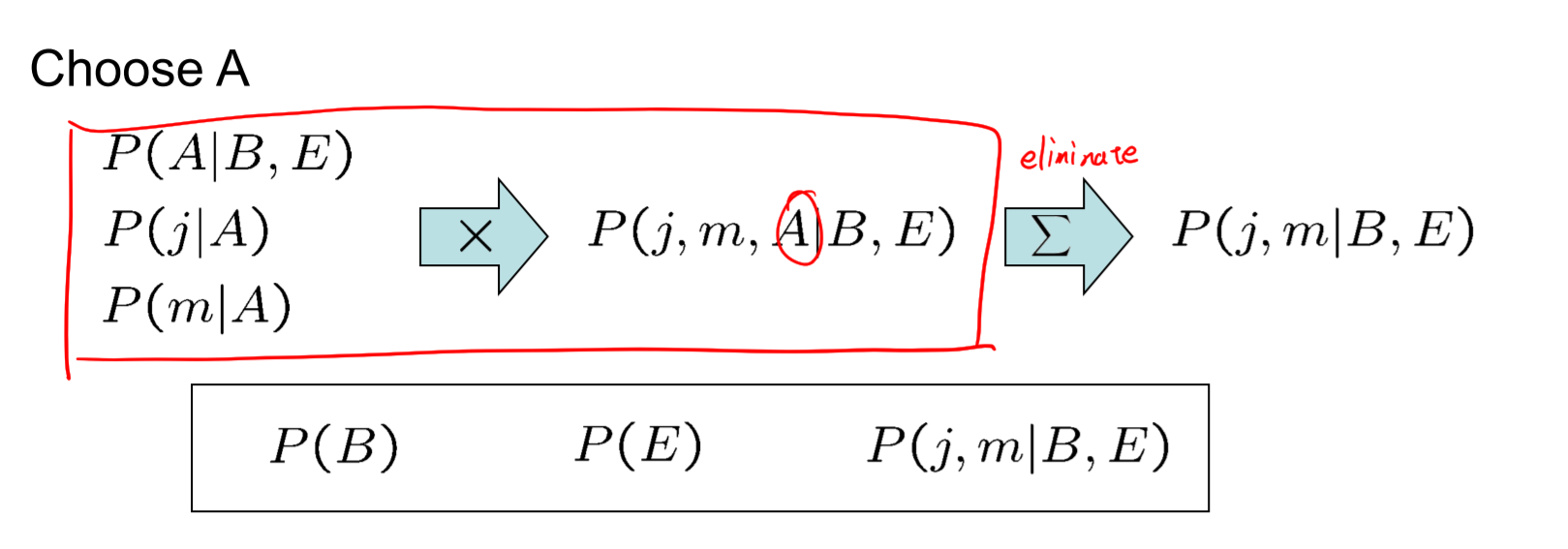
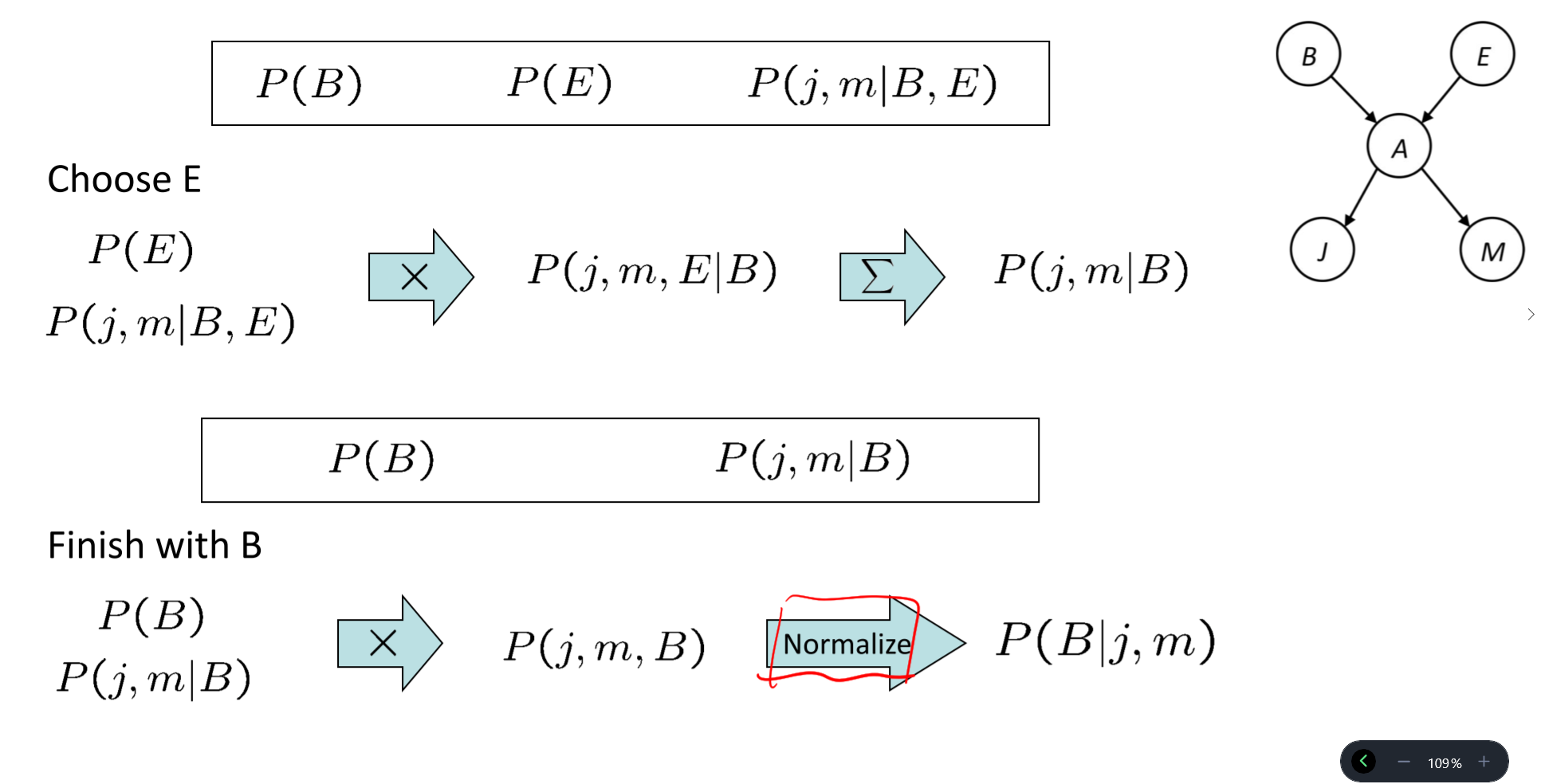
贝叶斯网络:取样(Sampling)
- 取样(Sampling):取样是一个重复模拟的过程
- 基本思路:
- 从取样的分布S中抽取N个样本
- 计算近似的概率
- 收敛至正确的概率
- 意义:
- 学习:从不知道的分布中获得样本
- 推断:获得样本比直接计算正确的概率要快
Prior Sampling
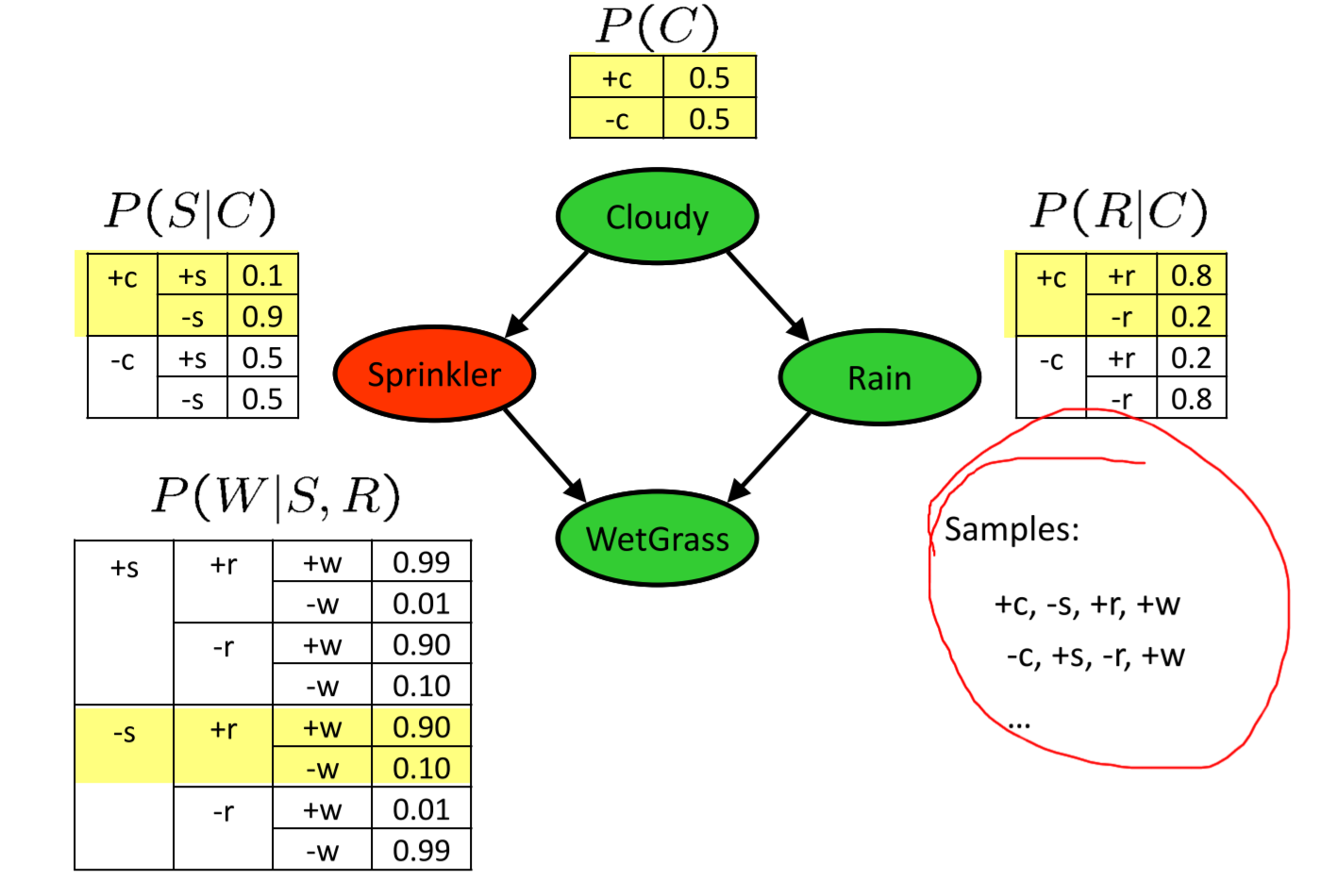 - 产生各个样本的概率为:\(\(S_{PS}(x_1...x_n)=\prod^n_{i=1}P(x_i|Parents(X_i))=P(x_1...x_n)\)\)
- 当样本数量足够多后,获得的概率就会收敛于真实值
- 产生各个样本的概率为:\(\(S_{PS}(x_1...x_n)=\prod^n_{i=1}P(x_i|Parents(X_i))=P(x_1...x_n)\)\)
- 当样本数量足够多后,获得的概率就会收敛于真实值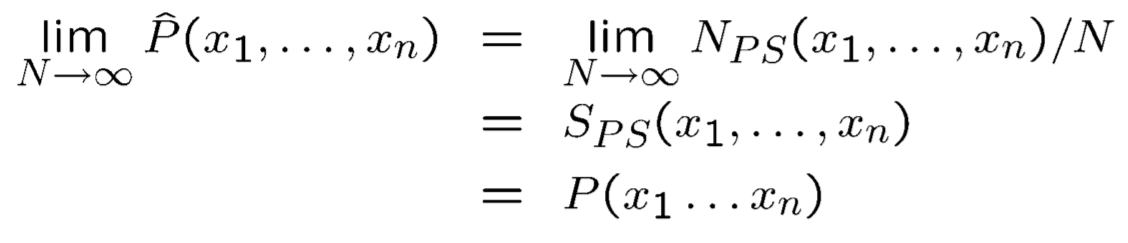 - 案例:
- 案例:
Rejection Sampling
- 如果有一个预先确定好的evidence,在选择采样结果时,可以忽略不符合evidence的样本

- 问题:
- 当evidence几乎不可能时,会拒绝大量的样本,产生大量无用的样本
- 在取样时,evidence并没有被利用
Likelihood Weighting
- 思路:处理evidence,让所有的样本都符合evidence
- weight bt probability of evidence given parents
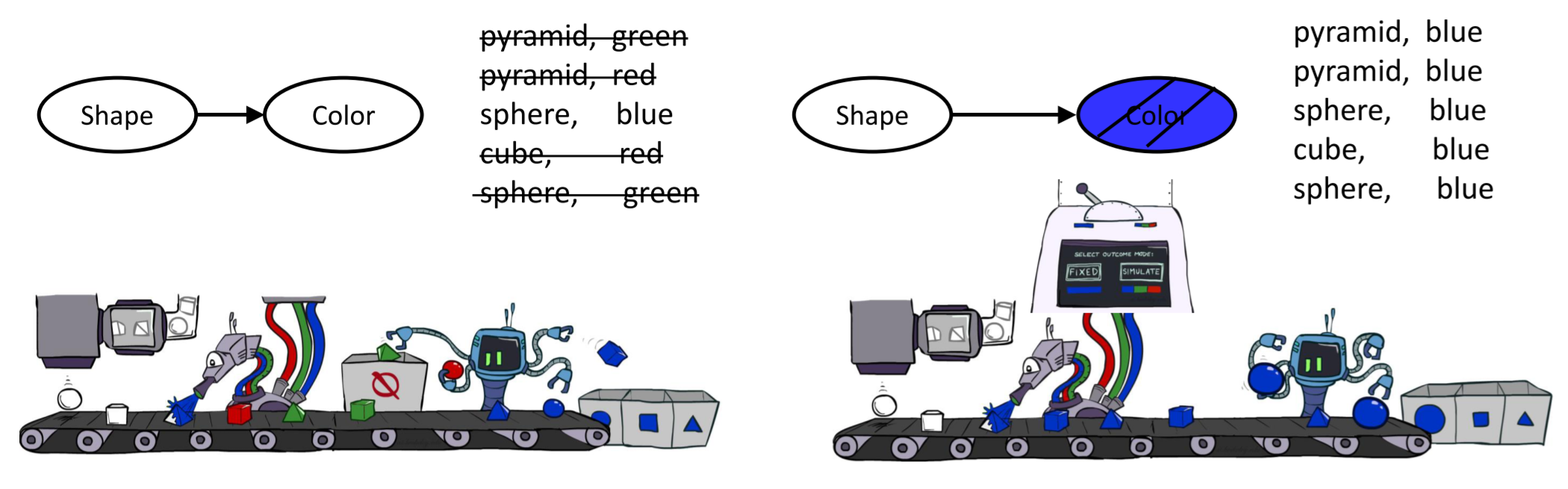

- weight bt probability of evidence given parents
- 针对z取样,e为evidence\(\(\begin{aligned} S_{WS}(z,e)=\prod^l_{i=1}P(z_i|Parents(Z_i)) \\ w(z,e)=\prod^m_{i=1}P(e_i|Parents(E_i)) \\ P(z,e)=S_{WS}(z,e)·w(z,e) \end{aligned}\)\)
- 优缺点:
- 优点:
- 考虑了evidence
- 更好的反映了在evidence影响下的世界
- 缺点:
- evidence可能会影响下游的随机变量的选择,导致出现错误的结果
- 优点:
Gibbs Sampling
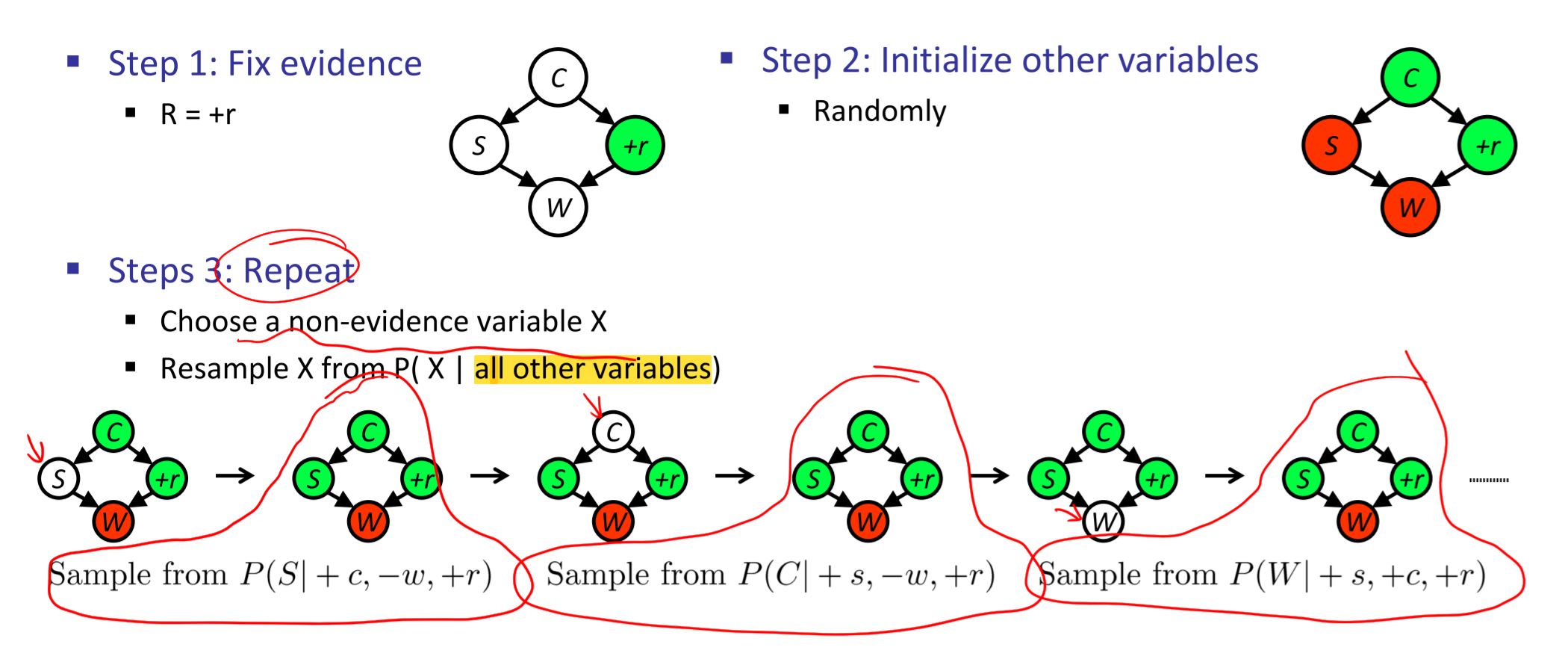
- 步骤:
- 确定evidence
- 初始化其他随机变量(随机初始化)
- 重复:
- 随机选择一个非evidence变量\(X\)
- 从\(P(X|all\ other\ variables)\)中取样