跳转至

隐马尔可夫模型(Hidden Markov Models-HMMs)

马尔可夫模型(Markov Models-MMs)

  • 引入了时间（或空间）的概念
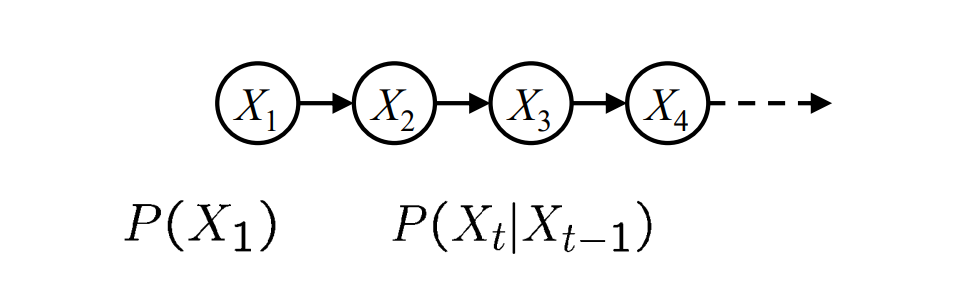
  • 属性：
    • 状态(State)：在时间\(t\)时\(X\)的值\(X_t\)
    • 参数(Parameters)：状态转移的概率
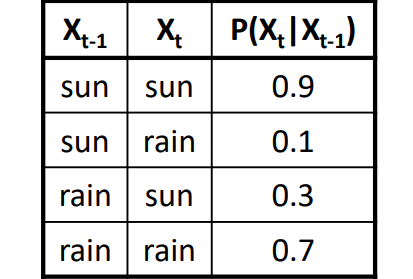
    • 稳定性假设(Stationary assumption)：在任意时间，转台转移函数总是相同的
    • 与MDP相比，没有行动(Action)的选择
  • 条件独立性：
    • \(Past\perp\!\!\!\perp Future | Present\)
    • 每一个时间步只取决于前一个状态（一阶马尔可夫性）
  • 案例：
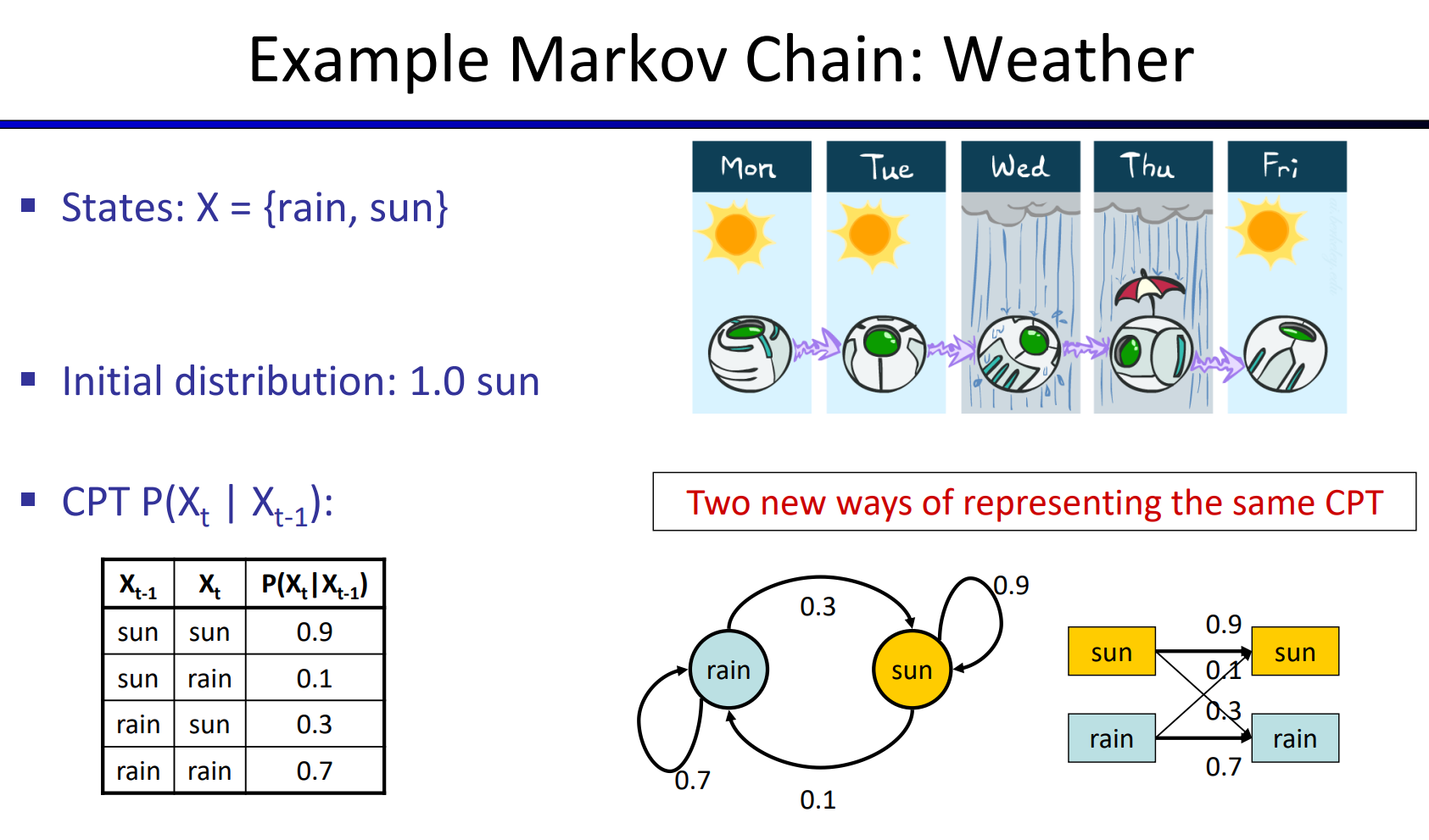
    • 初始化分布：
      • sun：1.0
      • rain：0.0
    • 下一步的计算\(P(X_2=sun)=P(X_2=sun|X_1=sun)P(X_1=sun)+P(X_2=sun|X_1=rain)P(X_1=rain)=0.9·1.0+0.1·0.0=0.9\) \(P(X_2=rain)=P(X_2=rain|X_1=sun)P(X_1=sun)+P(X_2=rain|X_1=rain)P(X_1=rain)=0.1·1+0.7·0.0=0.1\)
  • Mini-Forward Algorithm：\(P(x_t)=\sum_{w_i}Pr(w_i,W_{i+1})=\sum_{x_t-1}P(x_t|x_{t-1})P(x_{t-1})\)
    • 逐渐收敛至正确的值
  • Staionary Distribution：
    • 对于大多数的马尔可夫链，初始状态的影响会越来越小，并且最终状态与初始状态无关，满足\(P_\infty(X)=P_{\infty+1}(X)=\sum_xP(X|x)P_\infty(x)\)

隐马尔可夫模型(Hidden Markov Models-HMMs)

  • 隐马尔可夫模型：
    • 状态X上的基础马尔可夫链
    • 每一个时间步仅能观察到输出（影响）
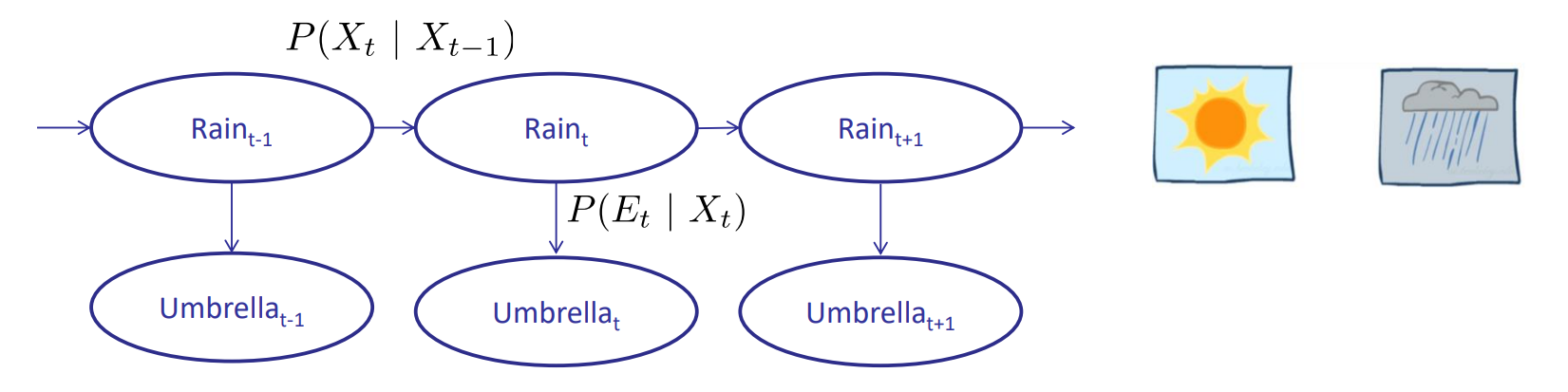
  • 包含：
    • 初始分布\(P(X_1)\)
    • 状态转移\(P(X_t|X_{t-1})\)
      • 与马尔可夫模型一样，是稳定的
    • 影响\(P(E_t|X_t)\)
      • 稳定的
  • 条件独立性：
    • 马尔可夫性：未来只取决于现在
    • 观测的结果只取决于当前的状态
    • 不同时间步获得的观测结果(evidence)之间并非独立<-之间由隐含的状态相关联
  • 应用：
    • 语音识别
    • 翻译
    • 机器人追踪
  • Belief Distribution
    • time i with all evidence \(f_1,f_2,...,f_i\)：\(B(W_i)=Pr(W_i|f_1,f_2,...,f_i)=Pr(W_i|f_{1:i})\)
    • time i with all evidence \(f_1,f_2,...,f_{i-1}\)：\(B^\prime(W_i)=Pr(W_i|f_1,f_2,...,f_{i-1})=Pr(W_i|f_{1:i-1})\)

前向算法(The Forward Algorithm)

  • Time Elapse Update(由\(B(W_i)\)确定\(B^\prime(W_{i+1})\))

    • 关键：时间步
    • 推导：
      • \(B(W_i)\)与\(B(W_{i+1})\)的关系(方法：mini-forward algorithm)\(\(B^\prime(W_{i+1})=Pr(W_{i+1}|f_{1:i})=\sum_{w_i}Pr(W_{i+1}|w_i,f_{1:i})Pr(w_i|f_{1:i})\)\)
      • \(B(W_i)=Pr(W_i|f_1,f_2,...,f_i)=Pr(W_i|f_{1:i})\) && \(W_{i+1}\perp\!\!\!\perp f_{1:i}|W_i\)：\(\(B^\prime(W_{i+1})=\sum_{w_i}Pr(W_{i+1}|w_i)B(w_i)\)\)
    • 案例：

  • Observation Update(由\(B^\prime(W_{i+1})\)确定\(B(W_{i+1})\))

    • 关键：观察evidence前后
    • 推导：
      • \(B(W_{i+1})\)(方法：朴素贝叶斯)\(\(B(W_{i+1})=Pr(W_{i+1}|f_{1:i+1})=\frac{Pr(W_{i+1},f_{i+1}|f_{1:i})}{Pr(f_{i+1}|f_{1:i})}\)\)
      • 对于任意的\(B(W_{i+1})\)，\(Pr(f_{i+1}|f_{1:i})\)为常数\(\(B(W_{i+1})\propto Pr(W_{i+1},f_{i+1}|f_{1:i})\)\)
      • 链式法则：\(\(B(W_{i+1})\propto Pr(W_{i+1},f_{i+1}|f_{1:i})=Pr(f_{i+1}|W_{i+1},f_{1:i})Pr(W_{i+1}|f_{1:i})\)\)
      • \(B^\prime(W_i)=Pr(W_i|f_1,f_2,...,f_{i-1})=Pr(W_i|f_{1:i-1})\) \(\(B(W_{i+1})\propto Pr(f_{i+1}|W_{i+1})B^\prime(W_{i+1})\)\)
      • 根据前向算法：\(\(B(W_{i+1})\propto Pr(f_{i+1}|W_{i+1})\sum_{w_i}Pr(W_{i+1}|w_i)B(w_i)\)\)
    • 案例：
  • 结合：

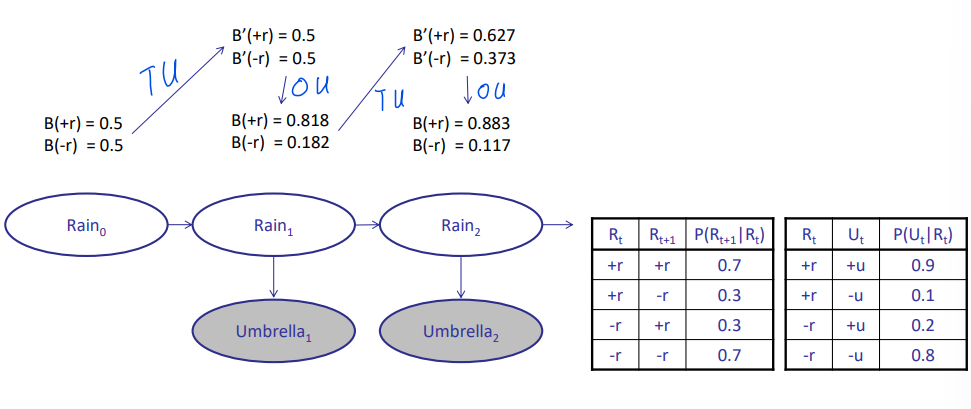
应用：粒子滤波(Particle Filtering)

  • 滤波(Filtering)：近似的解决方法
  • 粒子(Particle)：即样本的另一种称呼
  • 精确推理存在的缺陷：
    • 状态数量过多而难以存储B(X)
  • 解决方法：近似推理(Approximate Inference)
    • 存储粒子而非状态，并且存储大量的粒子，每一个粒子代表一个状态
  • \(n\ll d\)
    • n：the number of particles
    • d：the number of possible states
  • 使用\(P(x)\)近似的代表值为x的粒子数，即\(B(x)\)完全取决于状态x上粒子的数量

粒子滤波模拟(Particle Filtering Simulation)

  1. 初始化方法：
    1. 任意初始化
    2. 统一初始化
    3. 根据初始化概率进行初始化
  2. 两个更新方法：
    1. Time Elapse Update
      • 根据状态转移模型进行更新\(Pr(T_{i+1}|t_i)\)
    2. Observation Update
      • 使用感知模型\(Pr(F_i|T_i)\)来评估粒子
      • 过程：
        1. 计算所有粒子的权重
        2. 计算总权重
          1. \(total\ weight = 0\)：则重新进行初始化
          2. \(total\ weight \ne 0\)：归一化并且再取样
  3. 重复计算，直到分布收敛