DQN
在某些情况下，状态空间可能大得离谱（连续），对于这种情况，我们需要使用函数你和的方法来估计Q值，即将这个复杂的Q值表格视作数据，使用一个参数化的函数\(Q_\theta\)来拟合这些数据。 由于这样的方法存在一定的精度损失，因此被称为近似方法。
DQN(Deep Q Network)
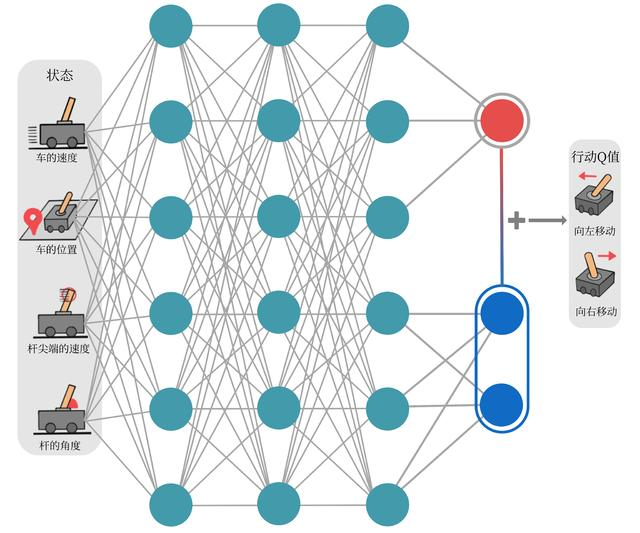
- 使用一个神经网络来表示函数\(Q\)
- 对于连续的动作：神经网络的输入是状态\(s\)和动作\(a\)，输出一个标量，表示在状态\(s\)下采取动作\(a\)所能获得的价值
- 对于离散的动作：可以只将状态\(s\)输入到神经网络中，使其同时输出一个动作的\(Q\)值
- 通常情况下：DQN只能处理离散的情况
- 在函数\(Q\)更新的过程中有\(max_a\)的操作
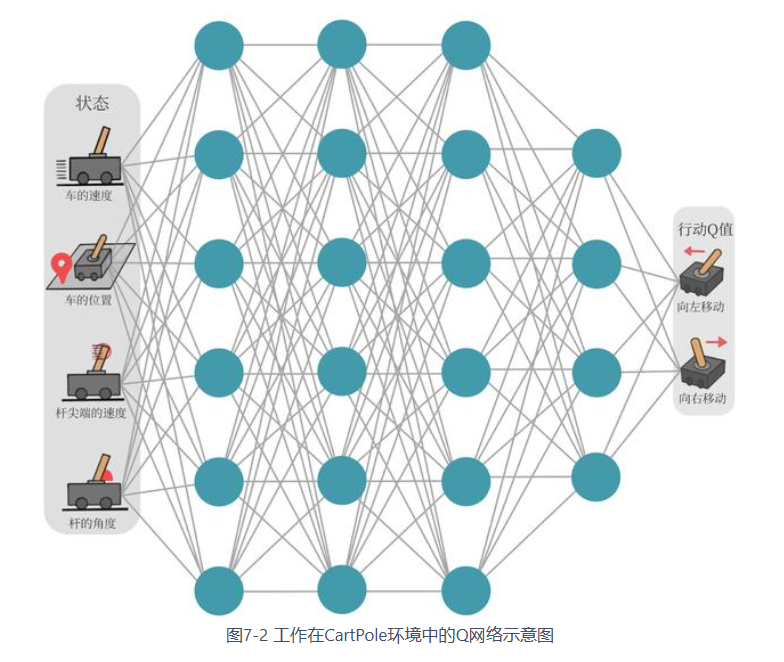
- 表示：假设神经网络用来拟合函数Q的参数是\(\omega\)，则使用\(Q_\omega(s,a)\)来表示每一个状态\(s\)下所有可能的动作\(a\)的\(Q\)值
- \(Q\)网络：用来拟合函数\(Q\)的神经网络
- Q网络的损失函数：$$ \omega ^{*}=arg \min \frac{1}{2N}\sum {i=1}^{N}\left[ Q{\omega}(s_{i},a_{i})-(r_{i}+ \gamma _{a{\prime}}Q_{\omega}(s_{i}{\prime},a^{\prime}))\right] ^{2}$$
由于DQN是离线策略算法，因此在收集数据时候可以使用一个\(\varepsilon\)-贪婪策略来平衡探索与利用
- DQN中两个重要的模块：
- 经验回放
- 目标网络
经验回放
在一般的有监督学习中，假设训练数据是独立同分布的，当我们每次训练神经网络的时候，从训练数据中随机采样一个或若干个数据来进行梯度下降，随着学习的不断进行，每一个训练数据会被使用多次。在原来的Q-Learning算法中，每一个数据只会用来更新一次Q值。 为了更好的将Q-Learning和深度神经网络结合，DQN算法使用了经验回放的方法 - 经验回放： 1. 维护一个回放缓冲区，将每次从环境中采样得到的四元组（状态、动作、奖励、下一个状态）数据存储到缓冲区中 2. 训练Q网络的时候，从缓冲区中进行随机采样 - 作用： - 使样本满足独立假设：在MDP交互过程中采样得到的数据不满足独立假设（因为当前时刻的状态与上一个时刻的状态有关），非独立同分布的数据对训练神经网络有很大的影响，会使神经网络拟合到最近训练的数据上。使用经验回放可以打破样本只将的相关性，使其满足独立假设 - 提高样本效率：每一个样本可以被使用多次，适合深度神经网络的梯度学习
目标网络
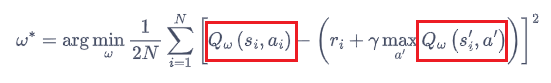- 目标网络：训练过程中Q网络的不断更新会导致目标不断发生改变，我们暂时先将TD目标中的Q网络固定住\(\leftarrow\)使用两套Q网络来实现
- 原训练网络\(Q_\omega(s,a)\)：用于计算损失函数\(\frac{1}{2}\left[ Q_{\omega}(s,a)-(r+ \gamma \ _{a^{\prime}}Q_{\omega^-}(s^{\prime},a^{\prime}))\right] ^{2}\)中所包含的\(Q_\omega(s,a)\)，并且使用正常的梯度下降方法来进行更新
- 目标网络\(Q_{\omega^-}(s,a)\)：用于计算损失函数\(\frac{1}{2}\left[ Q_{\omega}(s,a)-(r+ \gamma \ _{a^{\prime}}Q_{\omega^-}(s^{\prime},a^{\prime}))\right] ^{2}\)中所包含的\(Q_{\omega^-}(s,a)\)
- 如果两套网络的的参数随时保持一致，则仍然为原来的不稳定的网络。为了使更新目标更加稳定，目标网络并不会每一步都进行更新。在目标网络中使用一套较旧的参数：每隔C步，\(\omega\rightarrow \omega^-\)
具体流程
Double DQN
- 利用两套独立训练的神经网络来估计\(\max_{a^\prime}Q^*(s^\prime, a^\prime)\)
- 利用一套神经网络\(Q_\omega\)的输出来选取价值最大的动作，但在使用该动作的价值时，选择另一套神经网络\(Q_{\omega^-}\)来计算该动作的价值
- 优点：由于另一套神经网络的存在，这个动作最终使用的Q值也不会存在很大的过高的问题
- 具体实践：
- 将训练网络作为Double DQN算法中的第一套神经网络来选取动作
- 将目标网络作为第二套神经网络来计算\(Q\)值\(\(r+\gamma Q_{\omega^{-}}\left(s^{\prime}, \underset{a^{\prime}}{\arg \max } Q_{\omega}\left(s^{\prime}, a^{\prime}\right)\right)\)\)
Dueling DQN
在强化学习中，我们将动作价值函数\(Q\)减去状态价值函数\(V\)的结果定义为优势函数A，即\(A(s,a)=Q(s,a)-V(s)\) 在同一个状态下，所有动作的优势值之和为0 - 在Dueling DQN中，Q网络被建模为\(\(Q_{\eta, \alpha, \beta}(s, a)=V_{\eta, \alpha}(s)+A_{\eta, \beta}(s, a)\)\) - \(V_{\eta, \alpha}(s)\)为状态价值函数，\(A_{\eta, \beta}(s, a)\)为该状态下采取不同动作的优势函数，表示采取动作的差异性 - \(\eta\)是状态价值函数和优势函数共享的神经网络参数，一般用在神经网络中，用来提取特征的前几层 - \(\alpha\quad\beta\)分别为状态价值函数和优势函数的参数 - 在这样的模型下，我们不再让神经网络直接输出Q值，而是训练神经who最后几层的两个分支 - 分别输出状态价值函数和优势函数，再求得Q值
- 分别建模的好处：
- 某些情境下智能体只会关注状态的价值，而不关心不同动作导致的差异，此时将二者分开建模能够使智能体更好的处理动作关联较小的状态
- 在前方没有车的情况下，采取的动作之间并没有太大的差异
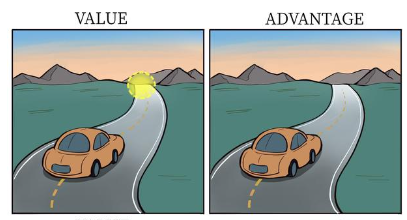
- 当前方有车时候，智能体才关注不同动作优势值之间的差异
- 在前方没有车的情况下，采取的动作之间并没有太大的差异
- 某些情境下智能体只会关注状态的价值，而不关心不同动作导致的差异，此时将二者分开建模能够使智能体更好的处理动作关联较小的状态