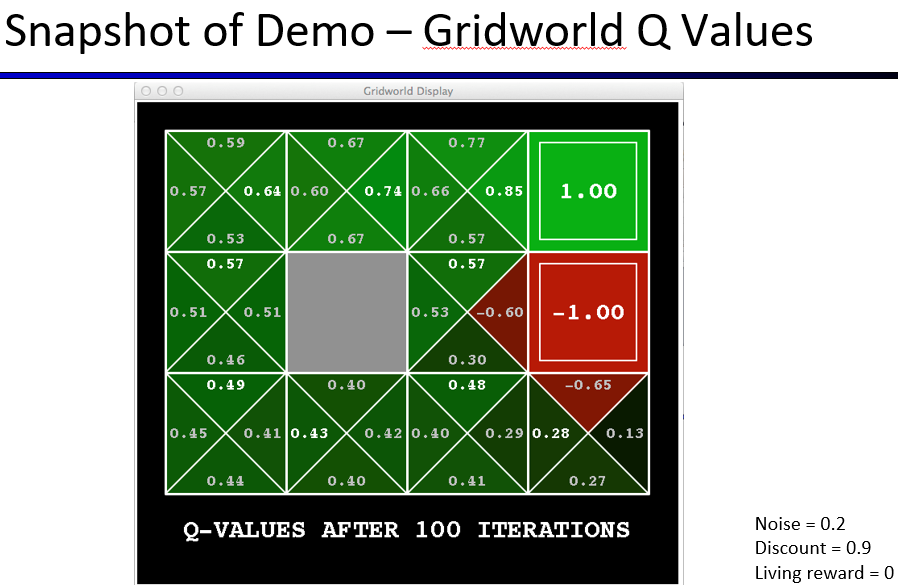
马尔可夫决策过程
- 不确定搜索问题：世界中存在一定程度的不确定性的问题被称为不确定搜索问题\(\rightarrow\)使用马尔可夫决策过程解决
马尔可夫奖励过程
\(<\mathcal{S},\mathcal{P},r,\gamma>\)属性
- 一个状态集\(\mathcal{S}\)
- 状态转移矩阵\(\mathcal{P}\)
- 奖励函数\(r\)
- 折扣因子\(\gamma\)
马尔可夫决策过程
\(<\mathcal{S},\mathcal{A},P,r,\gamma>\)属性：
- 一个状态集\(S\)
- 一个操作集\(A\)
- 一个起始状态
- 可能存在一个或多个最终状态
- 一个转换函数(transition function)\(T(state, action, state')\)： 表示任意状态执行任意行动后得到的各种输出的可能性
- 一个奖励函数(reward function)\(R(state, action, state')\)：： 表示任意状态执行任意行动后得到的各种输出的奖励
- 可能存在一个或多个最终状态
- 可能会有一个折扣因子(discount factor)\(\gamma\)
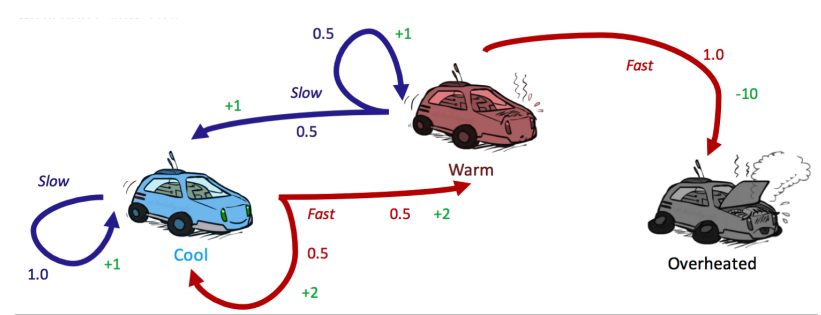
eg:
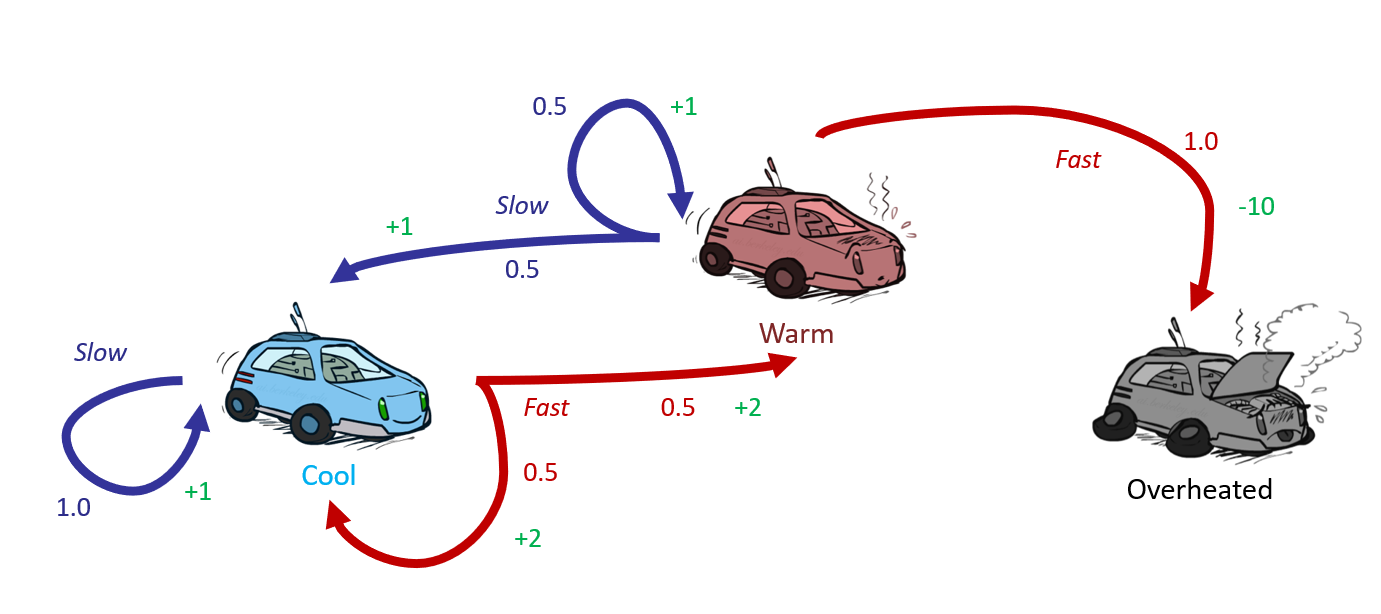- 三种状态：\(S=\{cool, warm, overheated\}\)
- 两种可能的操作：\(A=\{slow, fast\}\)
- 一个最终状态：Overheated
- 转移函数：\(T(state, action, state')\)
- \(T(cool, slow, cool) = 1\)
- \(T(warm, slow, cool) = 0.5\)
- \(T(warm, slow, warm) = 0.5\)
- \(T(cool, fast, cool) = 0.5\)
- \(T(cool, slow, warm) = 0.5\)
- \(T(warm, fast, overheated) = 1\)
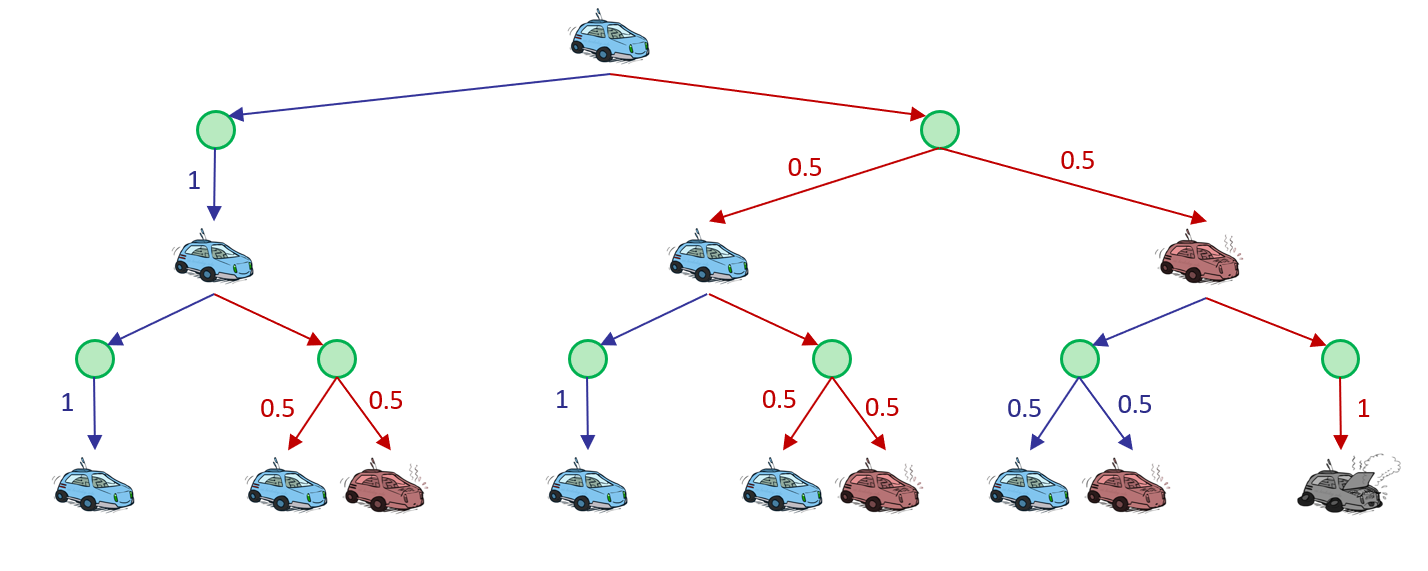- 奖励函数：\(R(state, action, state')\)
- \(R(cool, slow, cool) = 1\)
- \(R(warm, slow, cool) = 1\)
- \(R(warm, slow, warm) = 1\)
- \(R(cool, fast, cool) = 2\)
- \(R(cool, slow, warm) = 2\)
- \(R(warm, fast, overheated) = -10\)
- 一个agent的行动可以表示为：\(s_0 \overset{a_0} \rightarrow s_{1} \overset{a_1} \rightarrow s_{2}\overset{a_2} \rightarrow s_{3}……\)
- 其效益为：\(U([s_0, a_0,s_1, ,a_1,s_2,a_2,s_3…]) = R\left(s_{0}, a_{0}, s_{1}\right)+R\left(s_{1}, a_{1}, s_{2}\right) \\+R\left(s_{2}, a_{2}, s_{3}\right)+\ldots\)
由马尔可夫决策过程转化为马尔可夫奖励过程
- 边缘化：
- 对于某一个状态，我们根据策略将所有动作的概率进行加权，得到的奖励和就可以被认为是一个MRP在该状态下的奖励\(\(r^\prime(s)=\sum_{a\in\mathcal{A}}\pi(a|s)r(s,a)\)\)
- 同理可得MRP中的状态从\(s\)转移到\(s^\prime\)的概率：\(\(P^\prime(s^\prime|s)=\sum_{a\in\mathcal{A}}\pi(a|s)P(s^\prime|s,a)\)\) 即得到了一个MRP：\(<\mathcal{S},P^\prime, r^\prime, \gamma>\)
- 根据价值函数的定义可得，MDP的状态价值函数和转化后的MRP的价值函数是一样的，于是可以使用MRP中计算价值的函数来计算状态价值函数
无限效益
折扣因子(Discount Factors)
- 折扣因子\(\gamma(0<\gamma<1)\)表示奖励值随时间变化的指数衰减
- 现折扣后效益：\(U\left(\left[s_{0}, a_{0}, s_{1}, a_{1}, s_{2}, \ldots\right]\right)=R\left(s_{0}, a_{0}, s_{1}\right)+\gamma R\left(s_{1}, a_{1}, s_{2}\right)+\gamma^{2} R\left(s_{2}, a_{2}, s_{3}\right)+\ldots\)
- eg：\(\gamma = 0.1\)
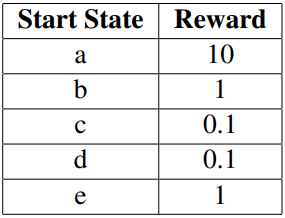
有限界（Finite Horizon）
- 类似于深度限制搜索(Depth-Limited Search)
- 在固定步数后结束“生命”
必然最终态(Absorbing State)
- 无论选择何种策略，最后必然达到一个最终状态(Terminal State)
状态价值函数与动作价值函数
状态价值函数
- 使用\(V^\pi(s)\)表示MDP中基于策略\(\pi\)的状态价值函数
- 它被定义为从状态\(s\)出发，遵循策略\(\pi\)能获得的期望回报\(\(V^\pi(s)=E_\pi[G_t|S_t-s]\)\)
动作价值函数
- 使用\(Q_\pi(s,a)\)表示MDP在遵循策略\(\pi\)时，对当前状态\(s\)执行动作\(a\)的到的期望回报：\(\(Q^\pi(s,a)=E_\pi[G_t|S_t=s,A_t=a]\)\)
二者之间的关系
- 在使用策略\(\pi\)时，状态s的价值等于在该状态下基于策略\(\pi\)采取所有动作的概率与响应的价值相乘再求和的结果：\(\(V^\pi(s)=\sum_{a\in \mathcal{A}}\pi(a|s)Q^\pi(s,a)\)\)
- 使用策略\(\pi\)时，状态下采取动作\(a\)的价值等于即时奖励加上经过衰减后的所有可能的下一个状态的状态转移概率与相应的价值的乘积\(\(Q^\pi(a,s)=r(a,s)+\gamma\sum_{s^\prime\in \mathcal{S}}P(s^\prime|s,a)V^\pi(s^\prime)\)\)
蒙特卡洛方法
- 蒙特卡洛方法：统计模拟方法，是基于概率统计的数值计算方法
- 使用随机抽样
- 然后运用概率统计方法来从抽样结果中归纳出我们想要得到的目标的数值估计
- 计算状态价值的具体过程
- 使用策略\(\pi\)采样若干序列：\(\(s_0 \overset{a_0} \rightarrow s_{1} \overset{a_1} \rightarrow s_{2}\overset{a_2} \rightarrow s_{3}……\)\)
- 对每一条序列中的每一时间步\(t\)的状态\(s\)进行以下操作
- 更新状态\(s\)的计数器\(N(s)\leftarrow N(s)+1\)
- 更新状态\(s\)的总回报\(M(s)\leftarrow M(s)+G\)
- 每一个状态的价值被估计为回报的期望：\(V(s)=\frac{M(s)}{N(s)}\)
另一种增量更新的方法： - \(N(s)\leftarrow N(s)+1\) - \(V(s)\leftarrow V(s)+\frac{1}{N(s)}(G-V(s))\)
最优量(Optimal Quantities)
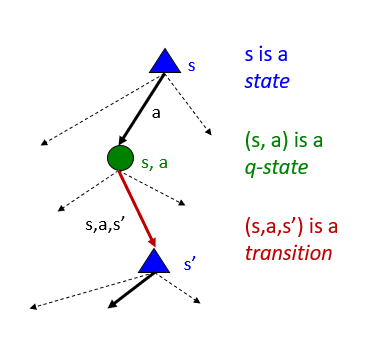1. state s：\(V^*(s)=\) 从状态s开始，剩余寿命中选择执行最优行为所获得的期望效益
2. q-state(s,a)：\(Q^*（s,a)=\) 状态s下选择执行行为a，并且获得最优结果的期望效益，并且从此后采取的都是最优行动
3. optimal policy：\(\pi^*(s)=\) 状态s下的最优行为
智能体的策略通常用字母\(\pi\)表示，策略\(\pi(a|s)=P(A_t=a|S_t=s)\)是一个函数，表示在输入状态为\(s\)的情况下采取动作\(a\)的概率 5. 价值(Value)的递归定义： $$ \begin{array}{l} V^{}(s)=\max _{a} Q^{}(s, a) \ Q^{}(s, a)=\sum_{s^{\prime}} T\left(s, a, s^{\prime}\right)\left[R\left(s, a, s^{\prime}\right)+\gamma V{*}\left(s{\prime}\right)\right] \ V^{}(s)=\max {a} \sum{s^{\prime}} T\left(s, a, s^{\prime}\right)\left[R\left(s, a, s^{\prime}\right)+\gamma V{*}\left(s{\prime}\right)\right] \end{array} $$ - egs:
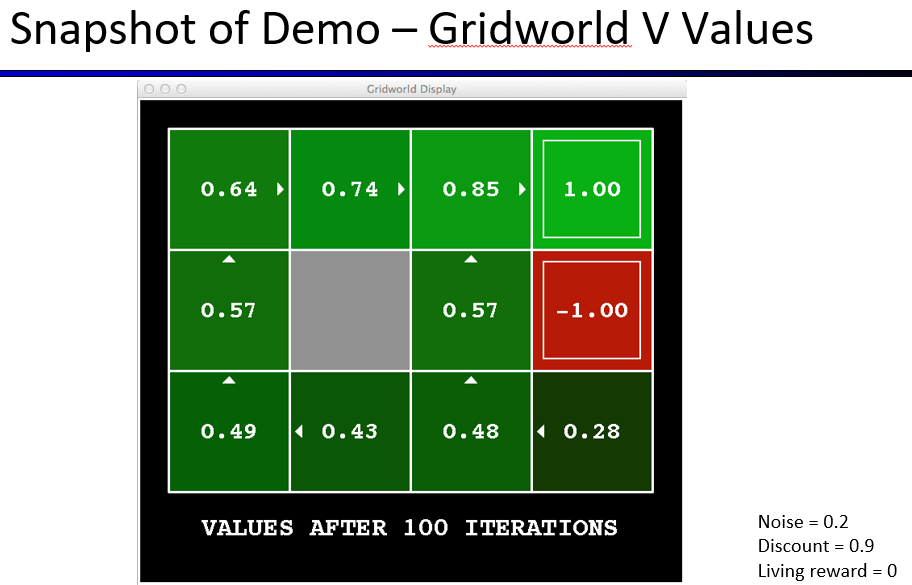
马尔可夫性（Markovianess）
- 马尔可夫性：过去与未来是条件独立的\(\rightarrow S_{t+1}\) 与 \(S_{t}\)之间存在关系，与先前无关，即只与最近的状态有关 \(P\left(S_{t+1}=s_{t+1} \mid S_{t}=s_{t}, A_{t}=a_{t}, S_{t-1}=s_{t-1}, A_{t-1}=a_{t-1}, \ldots, S_{0}=s_{0}\right)=P\left(S_{t+1}=s_{t+1} \mid S_{t}=s_{t}, A_{t}=a_{t}\right)\)
贝尔曼方程(Bellman Equations)
- 定义\(\(V^{*}(s)=\max _{a} \sum_{s^{\prime}} T\left(s, a, s^{\prime}\right)\left[R\left(s, a, s^{\prime}\right)+\gamma V^{*}\left(s^{\prime}\right)\right]\)\)
- Bellman Equation是动态规划的一个例子，这种方程可以通过其内在的递归结构将问题拆分成一个个小问题
值迭代(Value Iteration)
- 如何计算出最优值->限时值(time-limited value)
限时值(Time-limited Value)
- 限时值：强化有限界得到的结果
- 限制时间步数为\(k\)的一个状态\(s\)的限时值为\(V_k(s)\)，代表在已知当前MDP会在\(k\)时间步后终止的情况下，从s出发能得到的最大期望效益
- 执行流程：
- 初始化：\(\forall s \in S, V_0(s) = 0\)
- 重复如下更新操作：\(\forall s \in S, V_{k + 1}(s)=\max_{a}\sum_{s\prime}T(s,a,s\prime)[R(s,a,s\prime)+\gamma V_k(S\prime)]\)
- 通过计算子问题的解(所有\(V_k(s)\))来迭代得到更高一级的解(所有\(V_{k+1}(s)\))->动态规划算法
- 与Bellman方程的区别
- Bellman：给出最优化的条件
- 更新规则给出的是迭代更新值直至收敛的方法
- 达到收敛时，每个状态的Bellman方程都不会改变<-\(\forall s \in S, V(s)=V_{k+1}(s)=V^*(s)\)
eg
\(\gamma = 0.5\)
1. 初始化：
| cool | warm | overheated | |
|---|---|---|---|
| \(V_0\) | 0 | 0 | 0 |
| 2. 计算： | |||
 |
|||
 |
|||
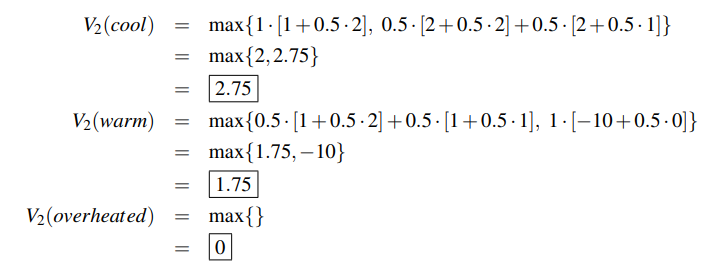| cool | warm | overheated | |
| :-----: | :----: | :----: | :----------: |
| \(V_0\) | 0 | 0 | 0 |
| \(V_1\) | 2 | 1 | 0 |
| \(V_2\) | 2.75 | 1.75 | 0 |
| ## 策略提取 | |||
| - 解决：如何确定最优策略？ | |||
| - 表达式：$$\forall s \in S, \pi^(s) = arg\max_aQ^(s,a)\ | |||
| =arg\max_a\sum_{s\prime}T(s,a,s^\prime)[R(s,a,s\prime)+\gamma V*(s\prime)$$ | |||
| - 其中\(a\)即为将我们带到具有最大Q-value的\(q\)状态操作 | |||
| ## 策略迭代 | |||
| - 值迭代存在的问题： | |||
| - 时间成本高：对每个q值得计算，需要轮流对 | S | 个状态再次进行迭代 | |
| - 进行了大量多余的计算<-策略提取得到的策略通常会比值本身更快的收敛 | |||
| - 策略迭代得操作： | |||
| - 定义一个初始策略 | |||
| - 可以随意确定，但是初始策略越接近最优策略，策列迭代收敛得越快 | |||
| - 重复以下操作： | |||
| 1. 评估：使用策略评估对当前得策略进行评估：\(V^\pi(s)\)表示期望效益 \(\(V^\pi(s)=\sum_{s^\prime}T(s,\pi(s),s^\prime)[R(s,\pi(s),s^\prime)+\gamma V^\pi(s^\prime)]\)\) | |||
| 2. 评估：利用以下更新规则，直至收敛：\(\(V_{k+1}^{\pi_{i}}(s) \leftarrow\sum_{s^{\prime}} T\left(s, \pi(s), s^{\prime}\right)\left[R\left(s, \pi_{i}(s), s^{\prime}\right)+\gamma V_{k}^{\pi_{i}}\left(s^{\prime}\right)\right]\)\) | |||
| 3. 提升：使用策略提取获得一个更好得策略：\(\(\pi_{i+1}(s)=arg\max_a\sum_{s\prime}T(s,a,s^\prime)[R(s,a,s\prime)+\gamma V^{\pi_i}(s^\prime)]\)\) | |||
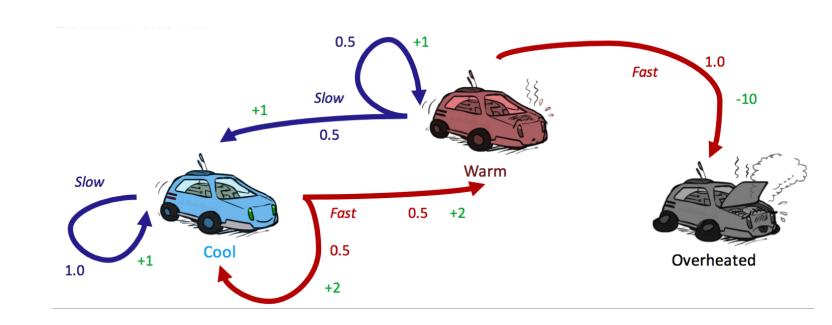
| ### eg： | |||
| \(\gamma = 0.5\) | |||
 |
|||
| - 任意确定初始状态： | |||
| cool | warm | overheated | |
| :-------: | :----: | :----: | :----------: |
| \(\pi_0\) | slow | slow | - |
| - 第一轮值迭代： | |||
 |
|||
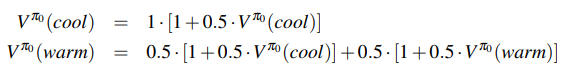| cool | warm | overheated | |
| :-----------: | :----: | :----: | :----------: |
| \(V^{\pi_0}\) | 2 | 2 | 0 |
| - 策略提取： | |||
 |
|||
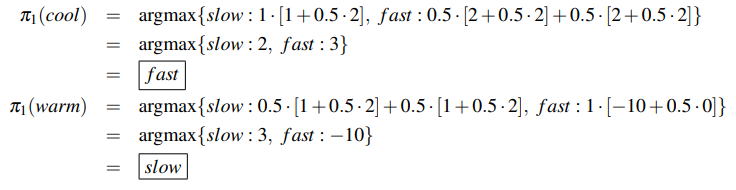| - 第二轮策略迭代可得\(\pi_2(cool)=fast,\pi_2(warm)=slow\) | |||
| - 与\(\pi_1\)策略相同，则\(\pi_1=\pi_2=\pi^*\) | |||
| cool | warm | ||
| :-------: | :----: | :----: | |
| \(\pi_0\) | slow | slow | |
| \(\pi_1\) | fast | slow | |
| \(\pi_2\) | fast | slow |