大物大题复习
速率分布函数
麦克斯韦速率分布率
速率分布函数
- 概率密度:\(f(v)=\frac{1}{N}\frac{dN}{dv}\)
- 物理意义:分子速率位与v附近单位速率区间内的分子数占总分子数的百分比
- 分子速率位于\(v\sim v+dv\)区间内的分子数占总分字数的百分比:\(f(v)dv=\frac{dN}{N}\)
- 分子速率位于\(v_1\sim v_2\)之间的数量为:\(\Delta N = N\int^{v_2}_{v_1}f(v)dv\)
\(\int^{\infty}_{0}f(v)dv=1\)
麦克斯韦速率分布律
- 平衡状态中气体分子速率分布函数:\(f(v)=4 \pi\left(\frac{m_{0}}{2 \pi k T}\right)^{3 / 2} \mathrm{e}^{-\frac{m_{0} v^{2}}{2 k T}} v^{2}\)
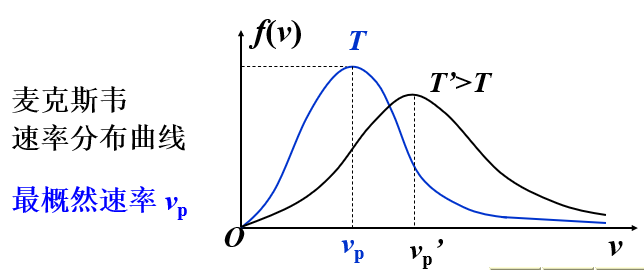
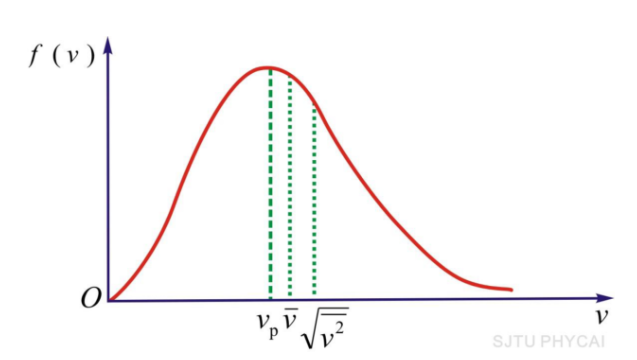
- 平衡态下三个分子速率的统计平均值
- 平均速率:\(\bar v = \int^{\infty}_{0}vf(v)dv\)
- 方均根速率:\(\frac{1}{2}m\bar{v^2}=\frac{3}{2}kT\rightarrow\sqrt{\bar{v^2}}=\sqrt{\frac{3kT}{m_0}}\approx1.71\sqrt{\frac{RT}{M}}=\sqrt{\int^{\infty}_{0}v^2f(v)dv}\)
- 最概然速率:\(v_p=\sqrt{\frac{2kT}{m_0}}\approx1.41\sqrt{\frac{RT}{M}}\)
分子碰撞和平均自由程
- 平均碰撞频率\(\bar Z\):1s内一个分子和其他分子碰撞的平均次数
- \(\bar Z = \sqrt 2 \pi d^2 \bar v n\)
- 平均自由程\(\bar \lambda\):没两次连续碰撞间一个分子自由运动的平均路程
- \(\bar \lambda=\frac{\bar v}{\bar Z}=\frac{1}{\sqrt2\pi d^2n}\)
理想气体热力学公式
[[热力学基础]]
卡诺循环
[[热力学基础#循环过程 卡诺循环]]
高斯定理
求电场、电势