跳转至

气体动理论

热运动的描述 理想气体模型和物态方程

状态参量

  • 体积V
  • 压强p
  • 温度T

    热力学温标(T:K)与摄氏温标(t:℃)：t = T + 273.15

平衡态 准静态过程

  • 平衡态：在不受外界影响的条件下，无论初始状态如何，系统的宏观性质在经充分长时间后不在发生变化的状态
    • 一定质量的气体的平衡态可以使用一组状态参量表示（p、V、T）
  • 准静态过程：当气体的外界条件改变时，气体中一个状态不断地变化到另一状态，如果状态变化过程进展的十分缓慢，使所经历的一系列中间状态，都无限接近平衡状态，这个过程叫做准静态过程

理想气体物态方程

理想气体：在任何情况下都严格遵守玻意耳定律、盖吕萨克定律以及查理定律的气体 - 当质量为m、摩尔质量为M的理想气体处于平衡态时，其状态参量满足方程（理想气体物态方程）： \(\(pV=\frac{m}{M}RT\)\) - 普适气体常量：\(R=8.31 J·mol^{-1}·K^{-1}\)

分子热运动和统计规律

分子热运动的图像

  • 分子热运动：大量分子做永不停息的无规则运动

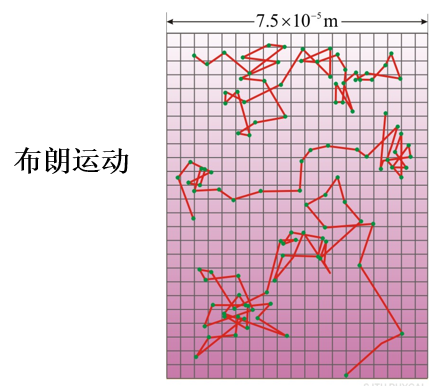
分子热运动的基本特征

  • 分子永恒运动与频繁的相互碰撞
  • 分布：正态分布

理想气体的压强和温度公式

理想气体的微观模型

  1. 力学假设：
    1. 将分子视作质点
    2. 除碰撞外，忽略其他的相互作用
    3. 气体分子在运动中遵守经典力学规律
    4. 忽略分子的重力
    5. 理想气体分子是自由地无规则地运动者的弹性质点群
  2. 统计假设：
    1. 平衡态时，气体分子数密度n平均分布
    2. 平衡态时，相同速率地分子沿各个方向运动地平均分子数相等

理想气体压强公式的推导

  • 大物公式 理想气体的压强：\(p=\frac{1}{3}nm_0\bar{v^2}\)

  • 大物公式 分子的平均平动动能：\(\bar{\varepsilon_k}=\frac{1}{2}m\bar{v^2}\)

  • 大物公式 理想气体的压强：\(p=\frac{1}{3}nm_0\bar{v^2}=\frac{2}{3}n(\frac{1}{2}m_0\bar{v^2})=\frac{2}{3}n\bar{\varepsilon_k}\)

温度的本质和统计意义

  • 大物公式 理想气体物态方程：\(pV=\frac{m}{M}RT=\frac{Nm_0}{N_Am_0}·RT=nkT\)(玻尔兹曼常量：\(k=\frac{R}{N_A}=1.38\times10^{-23}J·K^{-1}\))

  • 大物公式 \(\bar{\varepsilon_k}=\frac{1}{2}m\bar{v^2}=\frac{3}{2}kT\)

    • 温度的统计意义：温度标志着物体内部分子热运动的剧烈程度，是大量分子热运动的平均动能的统计平均值的度量

      对于单个分子，说其有温度是没有意义的

气体分子的方均根速率

  • 大物公式 方均根速率：\(\frac{1}{2}m\bar{v^2}=\frac{3}{2}kT\rightarrow\sqrt{\bar{v^2}}=\sqrt{\frac{3kT}{m_0}}=\sqrt{\frac{3RT}{M}}\)

能量均分定理 理想气体的内能

分子的自由度

  • 自由度：决定某物体在空间的位置所需要的独立坐标数目
  • 刚性气体分子的自由度
    • 单原子分子：
      • He、Ar
      • 三个自由度
    • 双原子分子：
      • H₂、O₂、N₂
      • 五个自由度
    • 多原子分子：
      • H₂O、CH₄
      • 六个自由度

能量均分定理

  • 大物公式 每个平动自由度都具有相同的平均动能：\(\frac{kT}{2}\)

  • 分子的平均动能：\(\bar{\varepsilon}=\frac{i}{2}kT\)
    • 单原子分子：\(\bar{\varepsilon}=\frac{3}{2}kT\)
    • 双原子分子：\(\bar{\varepsilon}=\frac{5}{2}kT\)
    • 多原子分子：\(\bar{\varepsilon}=\frac{6}{2}kT\)

理想气体的内能

  • 气体的内能：气体中所有分子的热运动动能和分子间相互作用势能的总和
  • 理想气体内能：气体中所有分子的平均动能的总和

  • 大物公式 质量为m，摩尔质量为M的理想气体内能：\(E=\frac{m}{M}E_0=\frac{m}{M}\frac{i}{2}RT\)

    一定量的理想气体，其内能只是温度的单值函数

麦克斯韦速率分布率

速率分布函数

  • 概率密度：\(f(v)=\frac{1}{N}\frac{dN}{dv}\)
    • 物理意义：分子速率位与v附近单位速率区间内的分子数占总分子数的百分比
  • 分子速率位于\(v\sim v+dv\)区间内的分子数占总分字数的百分比：\(f(v)dv=\frac{dN}{N}\)
  • 分子速率位于\(v_1\sim v_2\)之间的数量为：\(\Delta N = N\int^{v_2}_{v_1}f(v)dv\)

    \(\int^{\infty}_{0}f(v)dv=1\)

麦克斯韦速率分布律

  • 平衡状态中气体分子速率分布函数：\(f(v)=4 \pi\left(\frac{m_{0}}{2 \pi k T}\right)^{3 / 2} \mathrm{e}^{-\frac{m_{0} v^{2}}{2 k T}} v^{2}\)
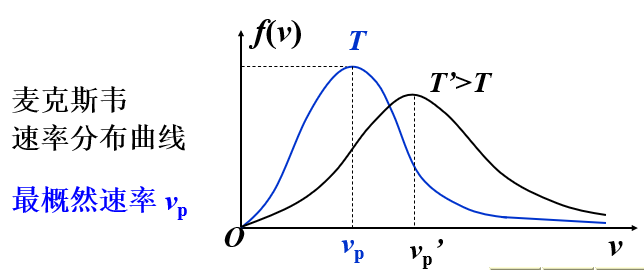
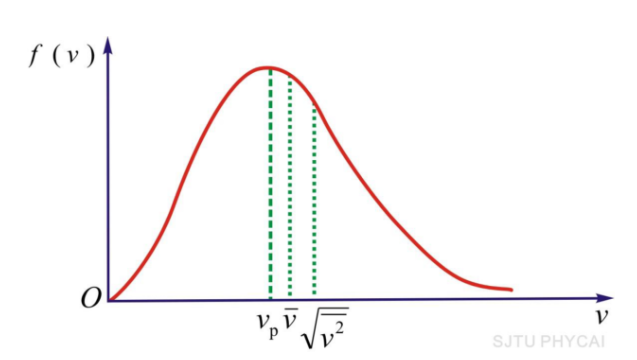
  • 平衡态下三个分子速率的统计平均值
    • 平均速率：\(\bar v = \int^{\infty}_{0}vf(v)dv\)
    • 方均根速率：\(\frac{1}{2}m\bar{v^2}=\frac{3}{2}kT\rightarrow\sqrt{\bar{v^2}}=\sqrt{\frac{3kT}{m_0}}\approx1.71\sqrt{\frac{RT}{M}}=\sqrt{\int^{\infty}_{0}v^2f(v)dv}\)
    • 最概然速率：\(v_p=\sqrt{\frac{2kT}{m_0}}\approx1.41\sqrt{\frac{RT}{M}}\)

分子碰撞和平均自由程

  • 平均碰撞频率\(\bar Z\)：1s内一个分子和其他分子碰撞的平均次数
    • \(\bar Z = \sqrt 2 \pi d^2 \bar v n\)
  • 平均自由程\(\bar \lambda\)：没两次连续碰撞间一个分子自由运动的平均路程
    • \(\bar \lambda=\frac{\bar v}{\bar Z}=\frac{1}{\sqrt2\pi d^2n}\)