热力学基础
热力学第零定律和第一定律
热力学第零定律
- 热力学第零定律:如果系统A、B同事和系统C达到热平衡,则系统A、B也处于热平衡——>热平衡的传递性
- 达到热平衡的系统具有共同的内部属性——温度
热力学过程
- 热力学系统:热力学中研究的物体或物体组
- 热力学过程:系统从一个平衡态过渡到另一个平衡态所经过的变化
- 分类:
- 准静态过程
- 非静态过程
功 热量 内能
- 内能的变化只与始末状态有关
- 改变系统状态的途径:
- 做功:外界有序能量与系统分子无序能量间的转换
- 传热:外界无序能量与系统分子无序能量间的转换
- 准静态做功的计算
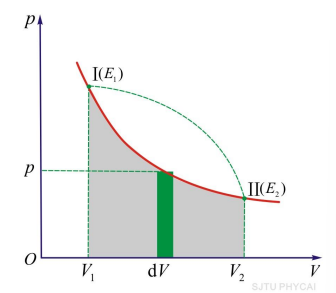
- 气体做功:\(dA = pSdl=pdV\rightarrow A=\int^{V^2}_{V^1}pdV\)
- 系统所做的功再树枝上等于P-V图上过程曲线以下的面积
热力学第一定律
\(\(Q=(E_2-E_1)+A=\Delta E + A\)\) - 热力学第一定律:外界对系统传递的热量,一部分使系统内能增加,一部分用于系统对外做功 - 正负号的规定 - 系统从外界吸热:Q>0 - 系统放热:Q<0 - 系统对外做功:A>0 - 外界对系统做功:A<0 - 微分形式:\(dQ=dE+dA\) - \(Q=E_2-E_1+\int^{V_2}_{V_1}pdV\)
热力学第一定律对于理想气体平衡过程的应用
等体过程气体的摩尔定容热熔
- 特征:V=常量
- 过程方程:\(\frac{p}{T}=常量\)
- 等体过程:
- \(Q=E_2-E_1=\frac{m}{M}\frac{i}{2}R(T_2-T_1)\)
- 在等体过程中,气体从外界吸热全部用来增加内能,对外没有做功
- 摩尔定容热容:\(C_{V,m}=\frac{(dQ)_V}{\frac{m}{M}dT}=\frac{dE}{\frac{m}{M}dT}=\frac{i}{2}R\)
- \(dE=\frac{m}{M}dTC_{V,m}\rightarrow E=\frac{m}{M}C_{V,m}T\)
- \(E=\frac{m}{M}\frac{i}{2}RT\rightarrow C_{V,m}=\frac{i}{2}R\)
[!NOTE] 摩尔定压热容:指在没有化学变化、相变化以及气体压强不变时,1mol气体温度的改变量为1K时热量的变化
等压过程气体的摩尔定容热容
- 特征:\(p=常量\)
- 过程方程:\(\frac{V}{T}=常量\)
- 等压过程:
- \(A_{p}=\int^{V_2}_{V_1}pdV=p(V_2-V_1)=\frac{m}{M}R(T_2-T_1)\)
- \(Q_p=E_2-E_1+A_p=\frac{m}{M}\frac{i}{2}R(T_2-T_1)+\frac{m}{M}R(T_2-T_1)\)
- 在等压过程中,气体从外界吸热,一部分转化为内能的增加,一部分转化为对外做功
- 摩尔定压热容:\(C_{p,m}=\frac{(dQ)_p}{\frac{m}{M}dT}=C_{V,m}+R=\frac{i+2}{2}R\)
- \((dQ)_p=dE+pdV=\frac{m}{M}dT·C_{p,m}\rightarrow dE=\frac{m}{M}C_{V,m}dT\)

- 比热容比:\(\gamma=\frac{C_{p,m}}{C_{V,m}}=\frac{2+i}{i}\)
- 单原子气体:\(i=3\rightarrow\gamma=1.67\)
- 刚性双原子气体:\(i=5\rightarrow\gamma=1.40\)
- 刚性多原子气体:\(i=6\rightarrow\gamma=1.33\)
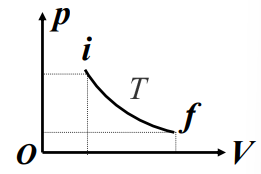
等温过程
- 特征:\(T=常量,dT=0\)
- 过程方程:\(pV=常量\)
- 对有限过程:
- \((Q)_T=(A)_T=\int^{V_2}_{V_1}\frac{m}{M}RT\frac{dV}{V}=\frac{m}{M}RT\ln{\frac{V_2}{V_1}}=\frac{m}{M}RT\ln{\frac{p_1}{p_2}}\)
- 在等温过程中,气体从外界吸热全部转化为对外做功,而气体的内能不变
绝热过程
- 特征:\(dQ=0\)
- 绝热过程方程:\(pV^\gamma=C_1\)

- 绝热线与等温线比较:压强下降更多
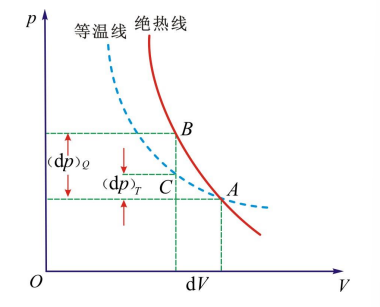
- 绝热线与等温线比较:压强下降更多
- 功能转换:
- 绝热过程:\(p_1V_1^\gamma=p_2V_2^\gamma=pV^\gamma=C_1\)
- 气体做功:\(A=\int^{V_2}_{V_1}pdV=\frac{p_2V_2-p_1V_1}{1-\gamma}=-\frac{m}{M}C_{V,m}(T_2-T_1)\)
- 内能变化:\(\Delta E=E_2-E_1=-A\)
总览

循环过程 卡诺循环
循环过程
- 特征:\(\Delta E=0\)
- 循环过程所作的净功大小等于p-V图上闭合曲线所包围的面积
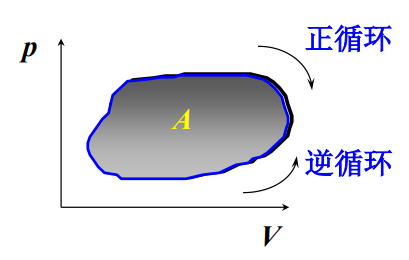
- 循环过程所作的净功大小等于p-V图上闭合曲线所包围的面积
- 正循环:
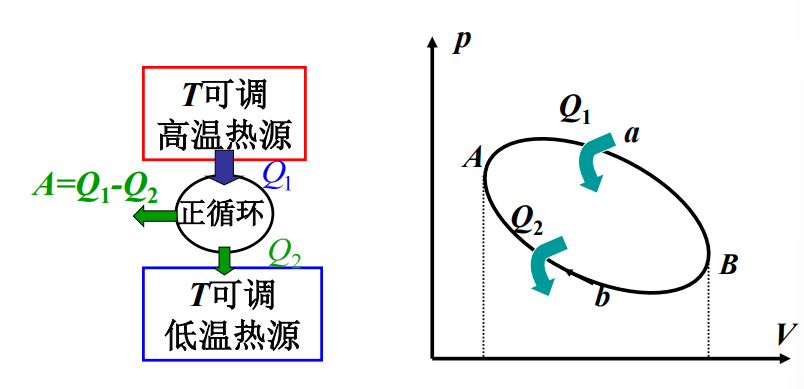
- 对应热机:把热转换为功的机器
- 热机效率:\(\eta=\frac{A}{Q_1}=1-\frac{Q_2}{Q_1}\)
- 逆循环:
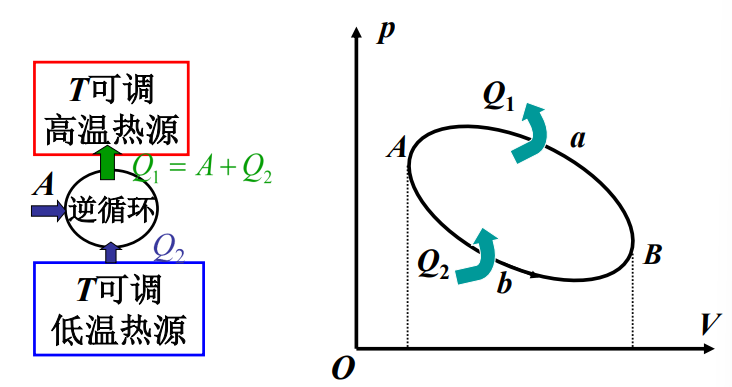
- 对应制冷机:利用外界做功获得低温的机器
- 制冷系数:\(w=\frac{Q_2}{A}=\frac{Q_2}{Q_1-Q_2}\)
卡诺循环
- 卡诺循环:由两个等温过程和两个绝热过程组成的准静态循环过程
- 卡诺热机效率:\(\eta _C=1-\frac{T_2}{T_1}\)
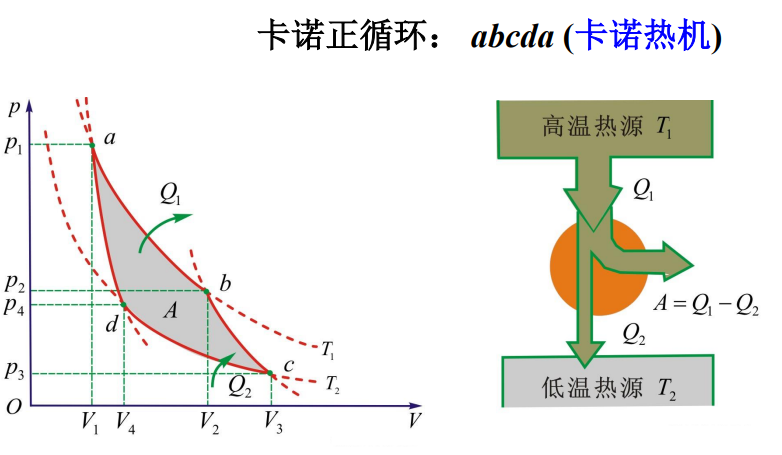
[!结论] - 最简单的循环过程 - 卡诺循环的效率仅仅由两热源的温度决定 - \(T_1 \uparrow, T_2 \downarrow \Rightarrow \eta \uparrow\) - \(\eta < 1\)
- 卡诺制冷机
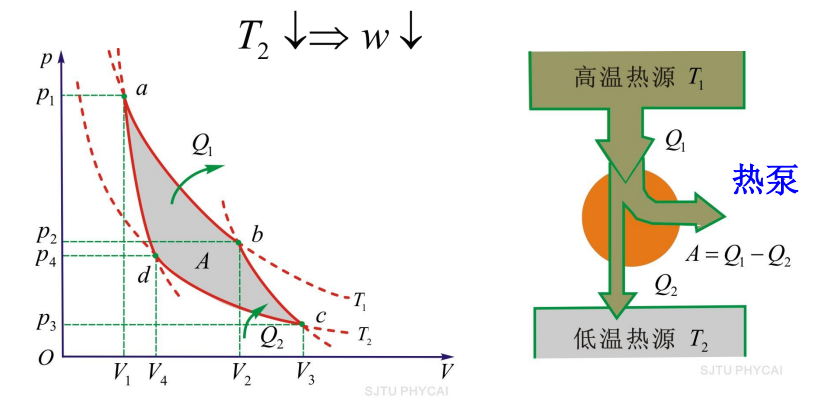
- 制冷系数:\(\omega=\frac{T_2}{T_1-T_2}\)
- \(T_2\downarrow \Rightarrow \omega \downarrow\)
- 制冷系数:\(\omega=\frac{T_2}{T_1-T_2}\)
热力学第二定律
两种描述:
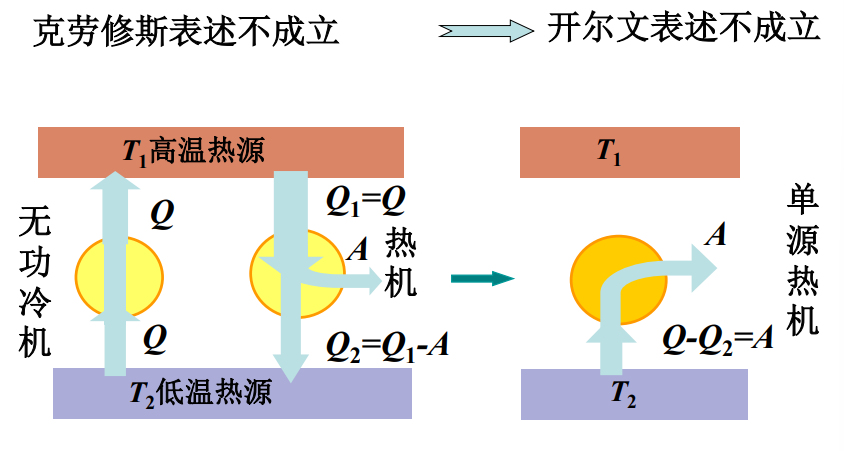
- 开尔文描述:不可能从单一热源吸收热量,使它完全转化为功,而不引起其他变化
- 指出了热功转换的方向性:功转化为热为自发过程
- 否定了第二类永动机或单源热机
- 克劳修斯描述:不可能把热量从低温物体传向高温物体,而不引起其他变化(热量不能自动地从低温物体传向高温物体)
- 指出了热传递的方向性:热量自动地从高温物体传向低温物体
- 无功冷机使不可能造成的
两种表述的等价性
- 反证法:
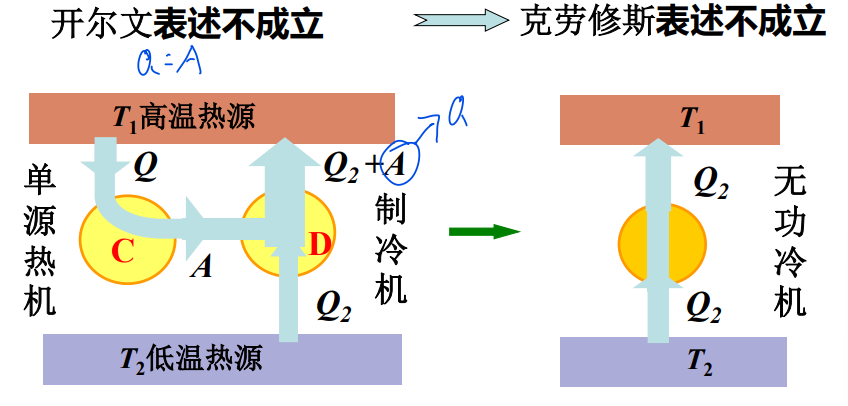
可逆过程与不可逆过程 卡诺定理
可逆过程与不可逆过程
- 可逆性判据:系统复原,外界也复原
- 如果系统不能恢复到原状态A,或者即使能恢复到原状态A,但周围一切不能恢复原状,也称为不可逆过程
一切实际的热力学过程都是不可逆过程
- 如果系统不能恢复到原状态A,或者即使能恢复到原状态A,但周围一切不能恢复原状,也称为不可逆过程
- 功热转换:
- 功转化为热的过程使不可逆的
- 如果出热力学过程中存在摩擦,此过程将是不可逆的
- 热传递
- 热量由高温物体传向低温物体的过程是不可逆的
- 热传导的不可逆性
- 气体的绝热自由膨胀的过程是不可逆的
- 非平衡态到平衡态的过程是不可逆的
- 快速做功过程为不可逆过程
- 热力学第二定律的实质指出,一切与热现象有关的实际宏观过程都是不可逆过程
- 只有无摩擦的准静态过程才是可逆过程
卡诺定理
- 可逆机:做可逆循环过程的机器
- 工作在相同的高温热源\(T_1\)和低温热源\(T_2\)之间的一切可逆机效率相同,与工作物质无关
- \(\eta_{可逆}=1-\frac{T_2}{T_1}\)
- 工作在相同的高温热源\(T_1\)和低温热源\(T_2\)之间的一切可逆机效率相同,与工作物质无关
- 不可逆机:做不可逆循环过程的机器
- 工作在其间的一切不可逆机的效率不大于可逆机
- \(\eta_{不可逆}\le 1- \frac{T_2}{T_1}\) ## 熵 玻尔兹曼关系 ### 熵