静止电荷的电场
物质的电结构 库伦定律
电荷

电荷守恒定律
- 在一个与外界没有电荷交换的系统内,无论进行怎样的物理过程,系统内正、负电荷量的代数和总是保持不变
点电荷的定义
- 物理学上把本身的线度比相互之间的距离小得多的带电体叫做点电荷。相当于运动学的“质点”模型
电荷的量子化
- 元电荷e的整数倍
库伦定律
- 库仑定律:真空中两个静止点电荷相互作用力的大小与这两个点电荷所带电荷量\(q_1\)和\(q_2\)的乘积成正比,与他们之间的距离\(r\)的平方成反比(\(\vec{F_{12}}=k\frac{q_1q_2}{r^2}\vec{e}_{r12}=k\frac{q_1q_2}{r^3}\vec{r}_{12}\)\)
- \(k=\frac{1}{4\pi\varepsilon_0}\)(由[[静止电荷的电场#静电场的高斯定理|高斯定理]]推导得)
静电场 电场强度
电场
 - 性质:
- 电荷在电场中要受到电场里的作用
- 电场里对电荷有做功的本领
- 性质:
- 电荷在电场中要受到电场里的作用
- 电场里对电荷有做功的本领
电场强度
- 电场强度:\(\vec{E}=\frac{\vec{F}}{q_0}\)
- \(\frac{\vec{F}}{q_0}\)与\(q_0\)无关
- 大小:\(\frac{\vec{F}}{q_0}\)
- 方向:试验电荷在该处所受到的电场力的方向
电场强度的计算
- 点电荷的电场强度(\(\vec{F}=\frac{qq_0}{4\pi\varepsilon_0r^2}\vec{e}_r\quad\vec{E}=\frac{q}{4\pi\varepsilon_0r^2}\vec{e}_r\)\)
- 方向:
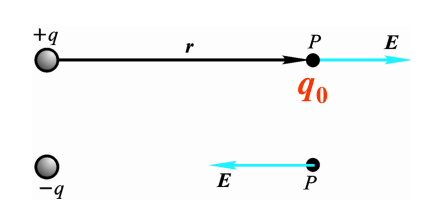
- 方向:
- 场强叠加原理:\(\vec{E}=\vec{E}_1+\vec{E}_2+\vec{E}_3+...+\vec{E}_n=\sum_i\vec{E}_i\)
- 例题:

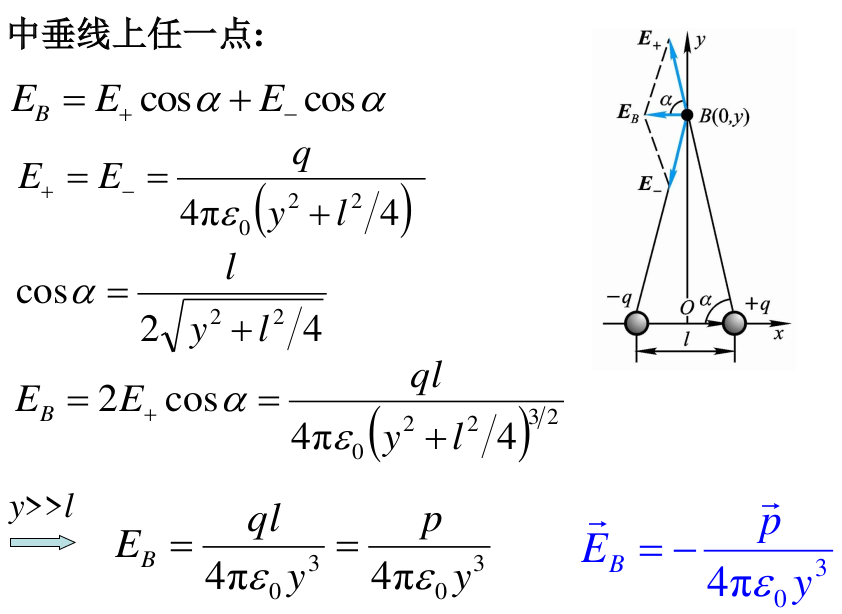
- 例题:
- 电荷连续分布带电体的电场强度
- 电荷元\(dq\)在\(P\)点的电场强度:(\(\mathrm{d} \vec{E}=\frac{\mathrm{d} q}{4 \pi \varepsilon_{0} r^{2}} \vec{e}_{r}\Rightarrow\vec{E}=\int \mathrm{d} \vec{E}=\int \frac{\mathrm{d} q}{4 \pi \varepsilon_{0} r^{2}} \vec{e}_{r}\)\)
- 体电荷:\(dq=\rho dV\)
- 面电荷:\(dq=\sigma dS\)
- 线电荷:\(dq =\lambda dl\)
- 例题:
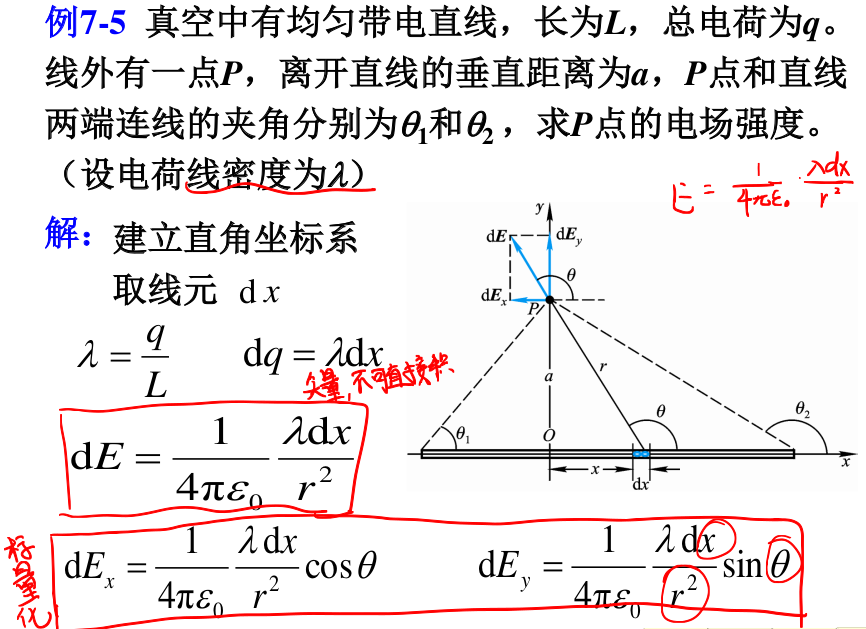
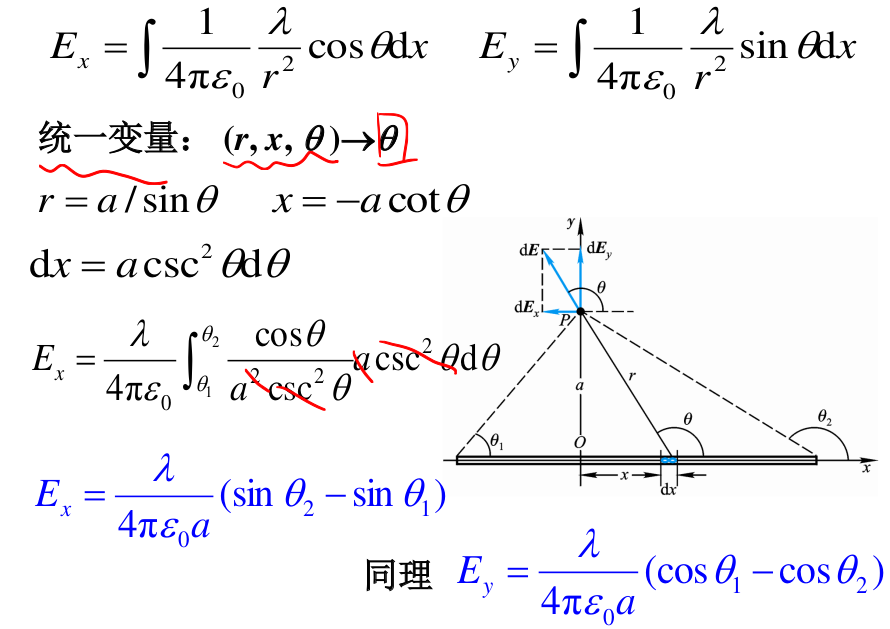
- 讨论:
- 无限长带电直线:\(E_x=0\quad E=E_y=\frac{\lambda}{2\pi\varepsilon_0a}\)方向向上
- 半无限长带电直线:\(E_x=E_y=\frac{\lambda}{4\pi\varepsilon_0a}\)
- 电荷元\(dq\)在\(P\)点的电场强度:(\(\mathrm{d} \vec{E}=\frac{\mathrm{d} q}{4 \pi \varepsilon_{0} r^{2}} \vec{e}_{r}\Rightarrow\vec{E}=\int \mathrm{d} \vec{E}=\int \frac{\mathrm{d} q}{4 \pi \varepsilon_{0} r^{2}} \vec{e}_{r}\)\)
- 特殊分布的情况:
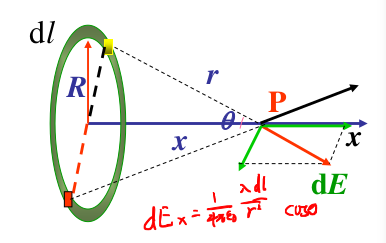
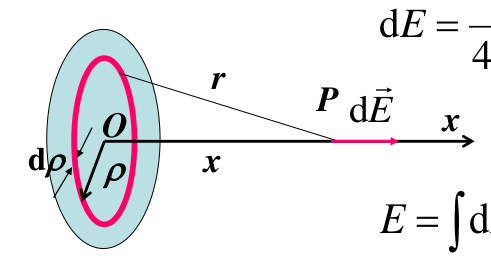
电场线 电场强度通量
- 电场强度大小:\(E=\frac{dN}{dS_\perp}\)
- 电场线的特点:
- 电场线起始于正电荷,终止于负电荷
- 电场线不闭合,不相交
- 电场线密集处电场强,稀疏处电场弱
- 电场强度通量\(\Phi_E\):通过电场中任一曲面的电场线条数
- 均匀电场中通过平面S的电场强度通量
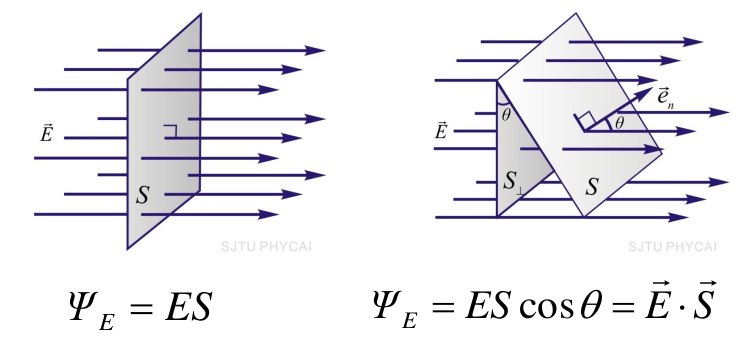
- 非均匀电场的电场强度通量
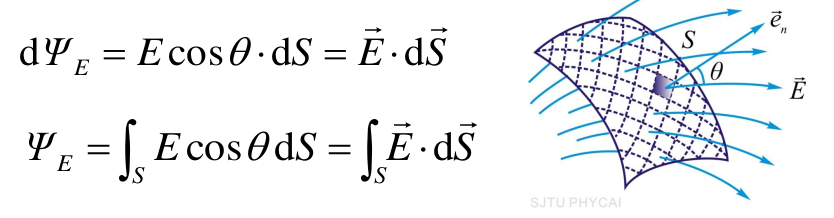
- 均匀电场中通过平面S的电场强度通量
静电场的高斯定理
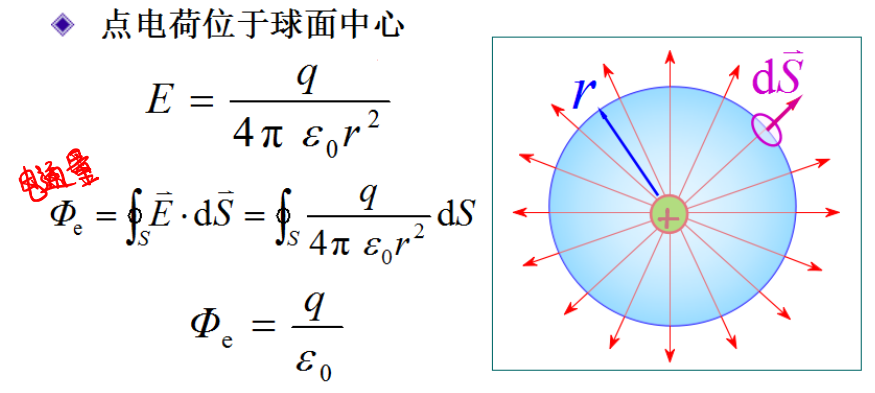 - 通过任一个包围点电荷的闭合曲面的电通量与曲面无关,结果都等于\(\frac{q}{\varepsilon_0}\)
- 一般的:
-
- 通过任一个包围点电荷的闭合曲面的电通量与曲面无关,结果都等于\(\frac{q}{\varepsilon_0}\)
- 一般的:
-  -
- 
[!NOTE] 闭合面内外的电荷对\(\vec{E}\)都有贡献,但是对于电通\(\oint_{S} \vec{E} \cdot d \vec{S}\)有贡献的只有面内电荷
