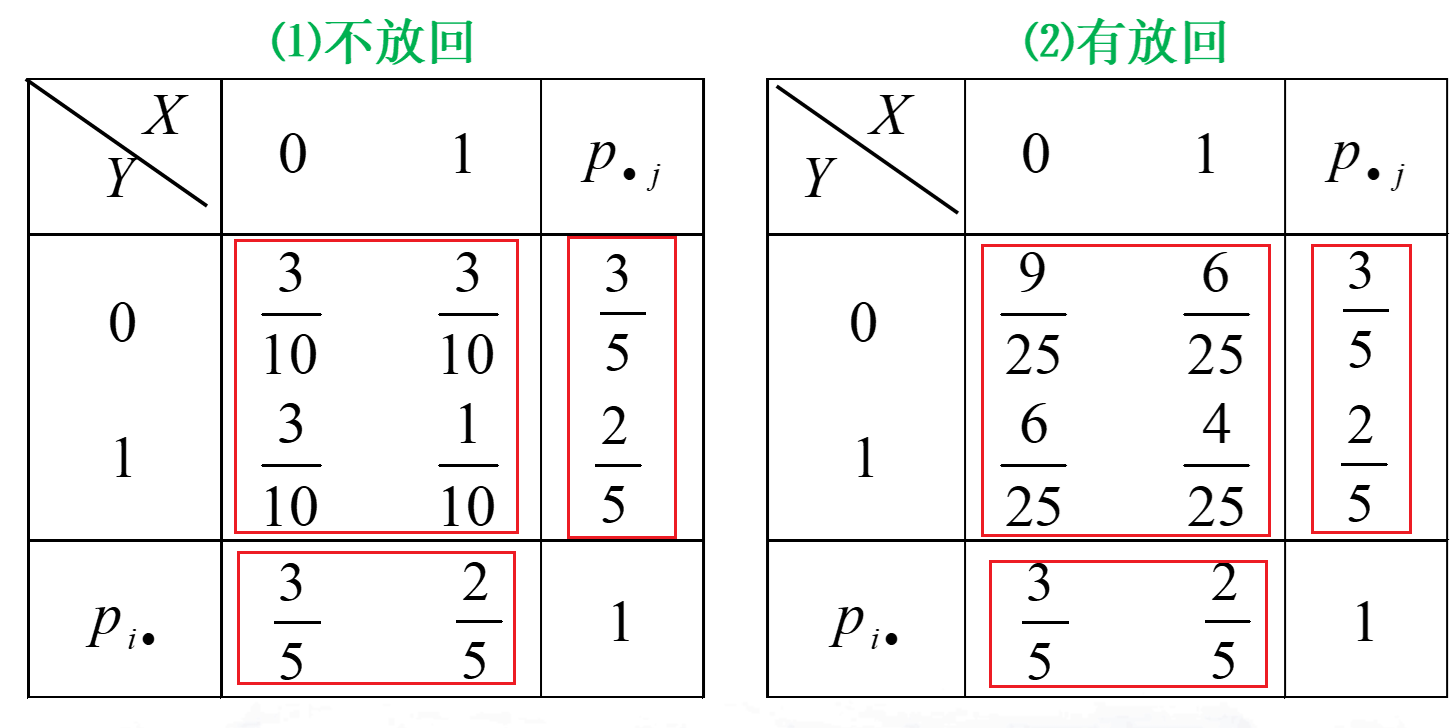
二维随机变量及其分布
二维随机变量及其分布函数
二维随机变量的概念
- 设随机试验\(E\)的样本空间\(\Omega=\{\omega|\omega为样本点\}\),\(X=X(\omega),Y=Y(\omega)\)分别为定义在\(\Omega\)上的随机变量,则称\((X,Y)\)为二维随机变量
[!问题] 为什么不分别研究\(X,Y\),二整体的研究\((X,Y)\)?? 分别研究不能体现\(X\)与\(Y\)之间的关系
二维随机变量的联合分布函数
- 联合分布函数:\(F(x,y)=P\{X\le x,Y\le y\},-\infty<x<+\infty,-\infty<y<+\infty\)
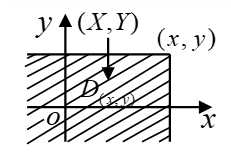
- \(F(x,y)\)在点\((x,y)\)出的取值为落入对应平面区域的概率
- 性质:

- \(P\{x_1< X\le x_2,y_1< Y \le y_2\}=F(x_2,y_2)-F(x_2,y_1)-F(x_1,y_2)+F(x_1,y_1)\)(根据面积推导)
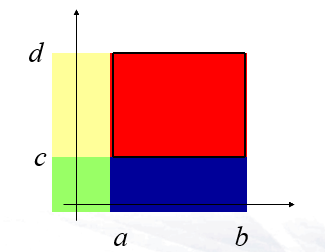
- \(P\{x_1< X\le x_2,y_1< Y \le y_2\}=F(x_2,y_2)-F(x_2,y_1)-F(x_1,y_2)+F(x_1,y_1)\)(根据面积推导)
二维离散型随机变量及其分布律
- 二维离散型随机变量:二维随机变量\((X,Y)\)的所有可能取值为有限个或可列无穷多个
- 列表:
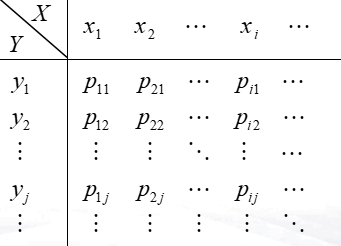
- \(P\{(X,Y)\in D\}=\sum_{(x_i,y_j)\in D}P_{ij}\),其中D为任一平面点集
- \(F(X,Y)=P\{X\le x,Y\le y\}=\sum_{x_i\le x}\sum_{y_i\le y}p_{ij},-\infty<x<+\infty,-\infty<y<+\infty\)
#概率论重点 二维连续型随机变量及其密度函数
二维连续型随机变量及其密度函数的概念
- \(F(x,y)=\int_{-\infty}^{x}\int_{-\infty}^{y}f(u,v)dudv\)
- \(f(x,y)\)为\((X,Y)\)的密度函数或联合密度函数
二维连续型随机变量密度函数的性质与有关结论
- 性质:满足以下性质,则为某二维连续型随机变量的密度函数
- \(f(x,y)\ge 0\)
- \(\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f(x,y)dxdy=1\)

- 结论
- 设二维连续型随机变量\((X,Y)\)的密度函数为\(f(x,y)\),则
- 在\(f(x,y)\)的连续点\((x,y)\)处,\(\frac{\partial^2F(x,y)}{\partial x\partial y}=f(x,y)\)
- 对于平面上任意区域D,有\(P\{(X,Y)\in D\}=\iint_{D}f(x,y)dxdy\)
- \(L\)为平面上的一条曲线:\(P\{(X,Y)\in L\} = 0\)

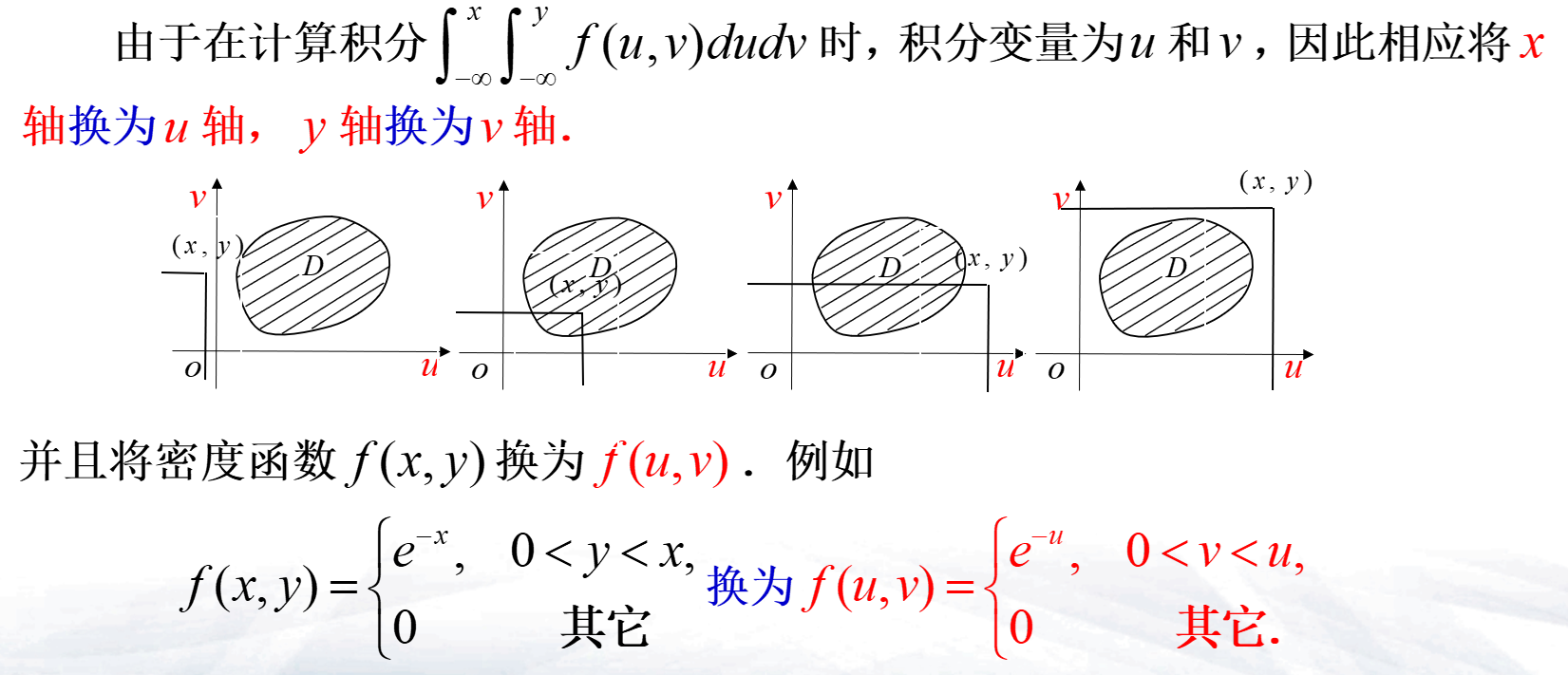
- \(L\)为平面上的一条曲线:\(P\{(X,Y)\in L\} = 0\)
- 设二维连续型随机变量\((X,Y)\)的密度函数为\(f(x,y)\),则
几种常见的二维连续型随机变量的概率分布
- 二维均匀分布(\(f(x,y)=\begin{cases}\frac{1}{S_D},(x,y)\in D\\0,(x,y)\notin D\end{cases}\)\)
- 记作:\((X,Y)\sim U(D)\)
- \(P\{(X,Y)\in G\}=P\{(X,Y)\in G \cap D\}=\frac{G\cap D的面积}{S_D}\)
- 二维正态分布(\(f(x, y)=\frac{1}{2 \pi \sigma_{1} \sigma_{2} \sqrt{1-\rho^{2}}} e^{-\frac{1}{2\left(1-\rho^{2}\right)}\left[\frac{\left(x-\mu_{1}\right)^{2}}{\sigma_{1}^{2}}-2 \rho \frac{\left(x-\mu_{1}\right)\left(y-\mu_{2}\right)}{\sigma_{1} \sigma_{2}}+\frac{\left(y-\mu_{2}\right)^{2}}{\sigma_{2}^{2}}\right]}\)\)
- 记作:\((X,Y)\sim N(\mu_1,\mu_2;\sigma_1^2,\sigma_2^2;\rho)\)
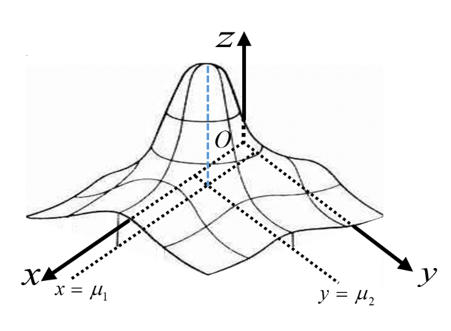
- 曲面关于直线\(\begin{cases}x=\mu_1\\y=\mu_2\end{cases}\)
- 记作:\((X,Y)\sim N(\mu_1,\mu_2;\sigma_1^2,\sigma_2^2;\rho)\)
#概率论重点 边缘分布
边缘分布的核心问题:利用(X,Y)的概率分布求X和Y的概率分布
二维随机变量的边缘分布函数
边缘分布可以由联合分布\((X,Y)\)来确定
二维离散型随机变量的边缘分布
\(\(\begin{aligned}P\left\{X=x_{i}\right\}=\sum_{j} p_{i j} \stackrel{\text { 记为 }}{=} p_{i \bullet}, \quad i=1,2, \cdots\\P\left\{Y=y_{j}\right\}=\sum_{i} p_{i j} \stackrel{\text { 记为 }}{=} p_{\bullet j}, j=1,2, \cdots\end{aligned}\)\)
- 将X和Y的边缘分布律添加到\((X,Y)\)分布律的列表得:
- 关于\(X\)的边缘分布率可从表中的\(p_{ij}\)进行纵向求和得
- 关于\(Y\)的边缘分布率可从表中的\(p_{ij}\)进行横向求和得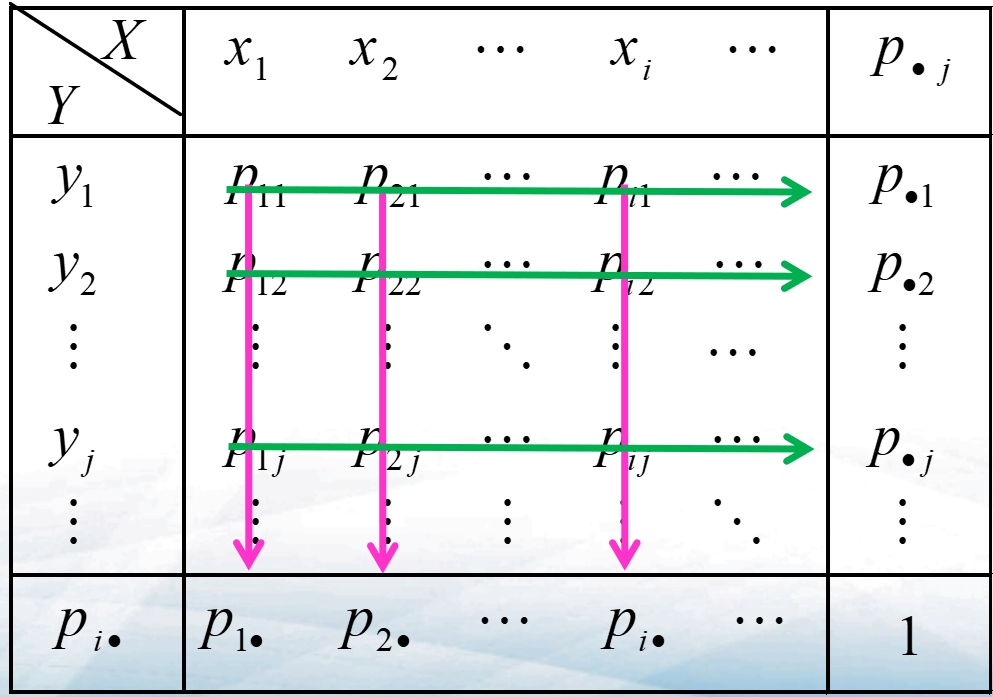
[!NOTE] 边缘分布率不能唯一确定联合分布律
#概率论重点 二维连续型随机变量的边缘密度函数
- 设\((X,Y)\)为二维连续型随机变量,分别称\(X\)和\(Y\)的密度函数为\((X,Y)\)关于\(X\)和\(Y\)的边缘密度函数,记为\(f_X(x)\)和\(f_Y(y)\)$$f_{X}(x)= \int {- \infty}^{+ \infty}f(x,y)dy,- \infty <x<+ \infty \quad f{Y}(y)= \int _{- \infty}^{+ \infty}f(x,y)dx,- \infty <y<+ \infty $$
- 证明:
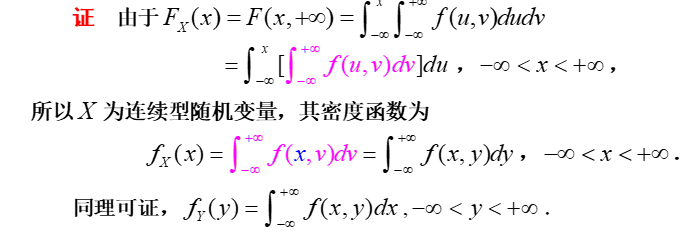
- 注:
- \(F_X(x)\)可通过在给定点\(x\)处,\(f(x,y)\)的对\(y\)从\(-\infty\)到\(+\infty\)(纵向)积分求得
- \(F_Y(y)\)可通过在给定点\(y\)处,\(f(x,y)\)的对\(x\)从\(-\infty\)到\(+\infty\)(横向)积分求得

- 证明:
条件分布
二维随机变量的条件分布函数

二维离散型随机变量的条件分布率
- 如果已知\(Y\)的取值为\(y\),且\(P \left\{ Y=y_{j}\right\} =p_{\cdot j}>0\),则称\(P \left\{ X=x_{i}|Y=y_{j}\right\} = \frac{p_{ij}}{p_{e.j}},i=1,2,\cdots\)为在条件\(Y=y_j\)下,\(X\)的条件分布率
- 如果已知\(X\)的取值为\(x\),且\(P \{ X = x _ { i } \} = p _ { i \cdot } \gt 0\),则称\(P \{ Y = y _ { j } | X = x _ { i } \} = \frac { P _ { i j } } { P _ { i } } , \quad j = 1 , 2 , \cdots\)为在条件\(X=x_i\)下,\(Y\)的条件分布率
- 条件分布率满足的性质:$$ \sum {i}\frac{p{ij}}{p_{\cdot j}}= \frac{\sum {i}p{ij}}{p_{\cdot j}}= \frac{p_{\cdot j}}{p_{\cdot j}}=1$$
- 条件分布率的表格形式:\(\(\begin{array}{l} \left(X \mid Y=y_{j}\right) \sim\left(\begin{array}{ccccc} x_{1} & x_{2} & \cdots & x_{i} & \cdots \\ \frac{p_{1 j}}{p_{\bullet j}} & \frac{p_{2 j}}{p_{\bullet j}} & \cdots & \frac{p_{i j}}{p_{\bullet j}} & \cdots \end{array}\right) \\ \left(Y \mid X=x_{i}\right) \sim\left(\begin{array}{lllll} y_{1} & y_{2} & \cdots & y_{j} & \cdots \\ \frac{p_{i 1}}{p_{i \bullet}} & \frac{p_{i 2}}{p_{i \bullet}} & \cdots & \frac{p_{i j}}{p_{i \bullet}} & \cdots \end{array}\right) \end{array}\)\)
二维连续型随机变量的条件密度函数
 - 定义:
- 如果已知\(Y=y\),且\(f_Y(y)>0\),则称\(f_{X|Y}(x|y)= \frac{f(x,y)}{f_{Y}(y)},- \infty <x<+\infty\)为在条件\(Y=y\)下,\(X\)的条件密度函数
- 如果已知\(X=x\),且\(f_X(x)>0\),则称\(f_{Y|X}(y|x)= \frac{f(x,y)}{f_{X}(x)},- \infty <y<+\infty\)为**在条件\(X=x\)下,\(Y\)的条件密度函数
- 定义:
- 如果已知\(Y=y\),且\(f_Y(y)>0\),则称\(f_{X|Y}(x|y)= \frac{f(x,y)}{f_{Y}(y)},- \infty <x<+\infty\)为在条件\(Y=y\)下,\(X\)的条件密度函数
- 如果已知\(X=x\),且\(f_X(x)>0\),则称\(f_{Y|X}(y|x)= \frac{f(x,y)}{f_{X}(x)},- \infty <y<+\infty\)为**在条件\(X=x\)下,\(Y\)的条件密度函数
[!注意] 对于二维连续型随机变量,不能使用第一张的条件概率计算公式计算 - \(P \left\{ a \leq X \leq b|Y=y_{0}\right\} = \int _{a}^{b}f_{X|Y}(x|y_{0})dx\) - \(P \left\{ c \leq Y \leq d|X=x_{0}\right\} = \int _{c}^{d}f_{Y|X}(y|x_{0})dy\)
- 根据条件密度函数与边缘分布密度函数求联合分布函数:\(f(x,y)=f_X(x)\cdot f_{Y|X}(y|x)=f_Y(y)\cdot f_{X|Y}(x|y)\)
#概率论重点 随机变量的独立性
随机变量相互独立的概念
- 随机变量\(X\)和\(Y\)相互独立是指\(X\)和\(Y\)的各自取值情况没有任何关系
- 相互独立:\(\(\left. \begin{array} { l } { P ( A _ { X } B _ { Y } ) = P ( A _ { x } ) P ( B _ { y} ) } \\ { P \{ X \leq x , Y \leq y \} = P \{ X \le { x }\} P \{ Y \leq y \} } \\ { F ( x , y ) = F _ { X } ( x ) F _ { Y } ( y ) } \end{array} \right.\)\)

离散型随机变量的独立性
- \(P \left\{ X=x_{i},Y=y_{j}\right\} =P \left\{ X=x_{i}\right\} P \left\{ Y=y_{j}\right\}\)即\(p_{ij}=p_{i\cdot}p_{\cdot j}\)
- \(X\)和\(Y\)相互独立的充要条件:\(p_{ij}=p_{i\cdot}p_{\cdot j},\quad i=1,2, \cdots ,j=1,2,\cdots\)

连续型随机变量的独立性
- 相互独立的充要条件:对于平面上几乎所有的点\((x,y)\),都有\(f(x,y)=f_{X}(x)f_{Y}(y)\)
[!注] 1. 平面上几乎所有的点是指平面上除去面积为0的点集之外的所有点\((x,y)\) 2. 如果存在平面区域\(D\),当\((x,y)\in D\)时,\(f(x,y)\neq f_{X}(x)f_{Y}(y)\),则\(X\)与\(Y\)不相互独立
- 是否独立的证明过程
- 由\(f(x,y)\)计算出边缘密度\(f_X(x)\)和\(f_Y(y)\)
- 然后判断\(f(x,y)\)与\(f_X(x)f_Y(y)\)的关系
- 设二维随机变量\((X,Y)\)的密度函数,其中\(a \leq x \leq b,c \leq y\)为区域\(D\),证明\(X\)与\(Y\)相互独立(\(f(x,y)= \left\{ \begin{matrix} f_1(x,y)=kg(x)h(y), \quad a \leq x \leq b,c \leq y \leq d \\ 0,其他 \\ \end{matrix} \right.\)\)
- 证明过程:
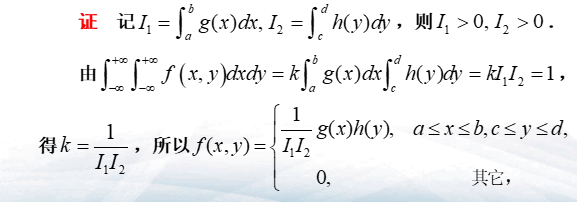
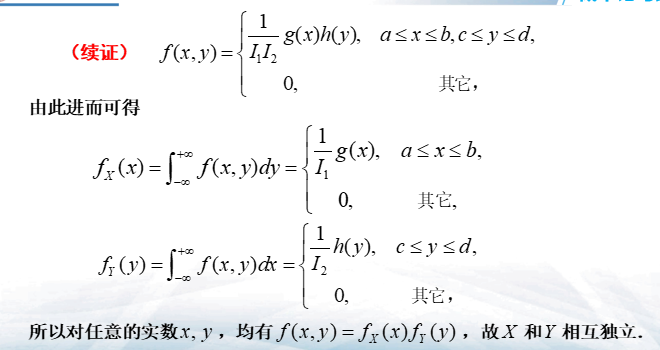
- 结论(不可直接使用)
- 如果\(D\)不是正矩形,则\(X\)与\(Y\)不互相独立
- 如果\(f_{1}(x,y)\neq g(x)h(y)\),则\(X\)与\(Y\)不互相独立
- 相反,则相互独立
- 证明过程:
随机变量独立性的有关结论
- 设随机变量\(X\)与\(Y\)相互独立,则对任意实数集合\(L_1,L_2\),有\(P \left\{ X \in L_{1},Y \in L_{2}\right\} =P \left\{ X \in L_{1}\right\} P \left\{ Y \in L_{2}\right\}\)

- 设随机变量\(X\)与\(Y\)相互独立,\(g(x),h(y)\)是连续函数,则随机变量\(g(x)\)与\(h(y)\)也相互独立
- 该逆命题并不成立
#概率论重点 二维随机变量函数的分布
当二维随机变量\((X,Y)\)的概率分布已知时,如何求出\(Z=g(X,Y)\)的概率分布
二维离散型随机变量的函数\(Z=g(X,Y)\)的概率分布
- \((X,Y)\)的分布律:\(\(\begin{array}{c|ccccc} (X, Y) & \left(x_{1}, y_{1}\right) & \left(x_{1}, y_{2}\right) & \ldots & \left(x_{i}, y_{j}\right) & \cdots \\ \hline P & p_{11} & p_{12} & \ldots & p_{i j} & \ldots \end{array}\)\)
- 求解步骤:
- 在\((X,Y)\)的分布律中添加一行\(Z=g(X,Y)\),并进行计算对应的值填入对应的行中
- 适当的进行合并,得到\(Z\)的分布律
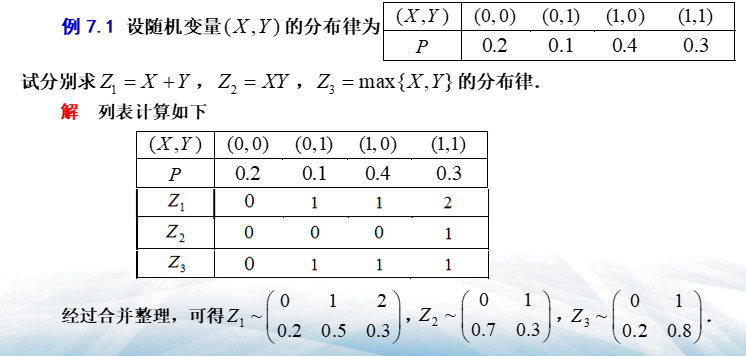
二维连续型随机变量的函数\(Z=g(X,Y)\)的概率分布
连续型的情况较为复杂: - \(Z=g(X,Y)\)可能为离散型 - \(Z=g(X,Y)\)可能为连续型 - \(Z=g(X,Y)\)可能为非离散型非连续型 - 当\(Z=g(X,Y)\)为连续型随机变量,或既非离散型,也非连续型随机变量时,通常使用分布函数法来求出\(Z\)的分布函数:\(\(F_{Z}(z)=P \left\{ Z \leq z \right\} =P \left\{ g(X,Y)\leq z \right\} = \iint _{g(x,y)\leq z}f(x,y)dxdy,- \infty <z<+\infty\)\) - 如果Z为连续型随机变量,则其密度函数为:\(f_Z(z)=F_Z^\prime(z),- \infty <z<+\infty\) [!难点] 在计算\(F_Z(z)\)的过程中,经常需要对变量\(z\)进行分段讨论

 - 设二维随机变量\((X,Y)\)的密度函数为\(f(x,y)\),则\(Z=X+Y\)的密度函数为\(\(f_{z}(z)= \int _{- \infty}^{+ \infty}f(x,z-x)dx \quad 或 \quad f_{z}(z)= \int _{- \infty}^{+ \infty}f(z-y,y)dy\)\)
- 卷积公式:如果\(X\)和\(Y\)相互独立,则\(Z=X+Y\)的密度函数为:\(\(f_{Z}(z)= \int _{- \infty}^{+ \infty}f_{X}(x)f_{Y}(z-x)dx \quad或\quad f_{Z}(z)= \int _{- \infty}^{+ \infty}f_{X}(z-y)f_{Y}(y)dy\)\)
- 结论(a、b为不全为0的常数):
- 设随机变量\(X\)和\(Y\)相互独立,且\(X\sim N(\mu_1, \sigma^2_1)\quad Y\sim N(\mu_2,\sigma_2^2)\),则\(aX+bY\sim N(a\mu_1+b\mu_2,a^2\sigma_1^2+b^2\sigma_2^2)\)
- 设二维随机变量\((X,Y)\sim N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)\),则aX+bY服从正态分布
- 设二维随机变量\((X,Y)\)的密度函数为\(f(x,y)\),则\(Z=X+Y\)的密度函数为\(\(f_{z}(z)= \int _{- \infty}^{+ \infty}f(x,z-x)dx \quad 或 \quad f_{z}(z)= \int _{- \infty}^{+ \infty}f(z-y,y)dy\)\)
- 卷积公式:如果\(X\)和\(Y\)相互独立,则\(Z=X+Y\)的密度函数为:\(\(f_{Z}(z)= \int _{- \infty}^{+ \infty}f_{X}(x)f_{Y}(z-x)dx \quad或\quad f_{Z}(z)= \int _{- \infty}^{+ \infty}f_{X}(z-y)f_{Y}(y)dy\)\)
- 结论(a、b为不全为0的常数):
- 设随机变量\(X\)和\(Y\)相互独立,且\(X\sim N(\mu_1, \sigma^2_1)\quad Y\sim N(\mu_2,\sigma_2^2)\),则\(aX+bY\sim N(a\mu_1+b\mu_2,a^2\sigma_1^2+b^2\sigma_2^2)\)
- 设二维随机变量\((X,Y)\sim N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)\),则aX+bY服从正态分布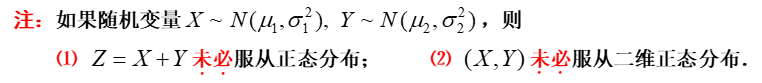 - 设二维随机变量\((X,Y)\)服从二维正态分布,\(\left\{ \begin{matrix} U=aX+bY \\ V=cX+dY \\ \end{matrix} \right.\),a,b,c,d为常数,且\(\begin{vmatrix}a \quad b \\ c \quad d \\ \end{vmatrix} =ad-bc \neq 0\),则\((U,V)\)服从二维正态分布
- #概率论重点 设随机变量\(X\)与\(Y\)相互独立,\(X\)的密度函数为\(f_X(x)\),分布函数为\(F_X(x)\);\(Y\)的密度函数为\(f_Y(y)\),分布函数为\(F_Y(y)\)\(\(M= \max \left\{ X,Y \right\} ,N= \min \left\{ X,Y\right\}\)\)则\(M\)与\(N\)的分布函数与密度函数分别为:\(\(\begin{array}{c}F_M(x)=F_X(x)F_Y(y) \\ f_M(x)=F_M^\prime(x)=f_X(x)F_Y(x)+F_X(x)f_Y(x) \\ F_N(x)=1-[1-F_X(x)][1-F_Y(x)] \\ f_N(x)=F_N^\prime(x)=f_X(x)[1-F_Y(x)]+f_Y(x)[1-F_X(x)]\end{array}\)\)
- 设二维随机变量\((X,Y)\)服从二维正态分布,\(\left\{ \begin{matrix} U=aX+bY \\ V=cX+dY \\ \end{matrix} \right.\),a,b,c,d为常数,且\(\begin{vmatrix}a \quad b \\ c \quad d \\ \end{vmatrix} =ad-bc \neq 0\),则\((U,V)\)服从二维正态分布
- #概率论重点 设随机变量\(X\)与\(Y\)相互独立,\(X\)的密度函数为\(f_X(x)\),分布函数为\(F_X(x)\);\(Y\)的密度函数为\(f_Y(y)\),分布函数为\(F_Y(y)\)\(\(M= \max \left\{ X,Y \right\} ,N= \min \left\{ X,Y\right\}\)\)则\(M\)与\(N\)的分布函数与密度函数分别为:\(\(\begin{array}{c}F_M(x)=F_X(x)F_Y(y) \\ f_M(x)=F_M^\prime(x)=f_X(x)F_Y(x)+F_X(x)f_Y(x) \\ F_N(x)=1-[1-F_X(x)][1-F_Y(x)] \\ f_N(x)=F_N^\prime(x)=f_X(x)[1-F_Y(x)]+f_Y(x)[1-F_X(x)]\end{array}\)\)

常见的二维连续性随机变量的分布
二维正态分布
- 联合密度函数:\(f(z_{1},z_{2})= \frac{1}{2 \pi}e^{- \frac{z_{1}^{2}+z_{2}^{2}}{2}}\)
- 将图形做仿射变换(平移、线性变换),得到一类图形所表示的密度函数就称为是二维正态分布的密度函数
- 正式定义:设\(Z_1,Z_2\)为独立同分布\(N(0,1)\)的随机变量,令\(\left\{ \begin{matrix} X= \sigma _{1}Z_{1}+ \mu _{1}\\ Y= \sigma _{2}(\rho Z_{1}+ \sqrt{1- \rho ^{2}}Z_{2})+ \mu _{2}\\ \end{matrix} \right. , \sigma _{1}>0, \sigma _{2}>0,| \rho |<1\),则称\((X,Y)\)服从参数为\((\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)\)的二维正态分布
- 记为:\((X,Y)\sim N(\mu _{1}, \mu _{2}, \sigma _{1}^{2}, \sigma _{2}^{2}, \rho)\)
- 矩阵形式:\(\begin{pmatrix}X \\ Y \\ \end{pmatrix} = \begin{pmatrix} \sigma _{1}&& 0 \\ \sigma _{2}\rho && \sigma _{2}\sqrt{1- \rho ^{2}}\\ \end{pmatrix} \begin{pmatrix} Z_{1}\\ Z_{2}\\ \end{pmatrix} + \begin{pmatrix} \mu _{1}\\ \mu _{2}\\ \end{pmatrix}\)
从密度函数看,\(X\)与\(Y\)的地位是对称的,去决定了他们的分布特点是一致的
- 边缘分布:
- \(X \sim N(\mu _{1}, \sigma _{1}^{2})\)
- \(Y \sim N(\mu _{2}, \sigma _{2}^{2})\)
- 注:两个边缘分布均与\(\rho\)无关
- 条件分布:
- \(Y|_{X=x}\sim N(\frac{\sigma _{2}\rho}{\sigma _{1}}(x- \mu _{1})+ \mu _{2}, \sigma _{2}^{2}(1- \rho ^{2}))\)
- \(X|_{Y=y}\sim N(\frac{\sigma _{1}\rho}{\sigma _{2}}(y- \mu _{2})+ \mu _{1}, \sigma _{1}^{2}(1- \rho ^{2}))\)
区域上的均匀分布
- 密度函数:\(f(x,y)= \left\{ \begin{matrix} \frac{1}{|S|},(x,y)\in S \\ 0, 其他\\ \end{matrix} \right.\)
"等可能"即在取值空间的每一点密度函数都是相等的 区域上的均匀分布常用来解决许多看似不像几何问题的实际问题