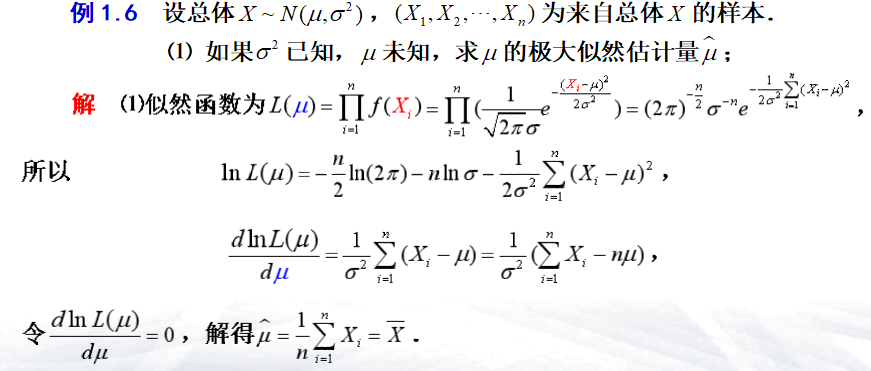参数估计

[!什么是参数估计] 参数通常是刻画总体某些概率特征的数量 例如正态分布\(N(\mu,\sigma^2)\)中的参数\(\mu\)就是该分布的均值,参数\(\sigma^2\)是该分布的方差 当参数未知时,从总体中抽取一个样本,用某种方法对未知参数进行估计,这就是参数估计 先从该总体中抽取样本\(X_1,X-2,...,X_n\),然后构造样本函数,求出未知参数\(\mu\)与\(\sigma^2\)的估计值([[参数估计#点估计|点估计]])或取值范围([[参数估计#区间估计|区间估计]])
点估计
点估计的概念
- 构造一个格式的统计量\(\hat{\theta}=\hat{\theta}(X_1,X_2,...,X_n)\)作为未知参数\(\theta\)的估计
- 统计学上称\(\hat{\theta}\)为\(\theta\)的估计量
- 对应于样本\((X_1,X_2,...,X_n)\)的每个观察值\((x_1,x_2,...,x_n)\),估计量\(\hat\theta\)的值\(\hat{\theta}(x_1,x_2,...,x_n)\)称为\(\theta\)的估计值
[!注] 估计量是统计量,一定依赖于样本
- 称\(\theta =(\theta _{1}, \theta _{2}, \cdots , \theta _{k})\)的取值范围为参数空间,记为\(\Theta\)
- 问题:
- 如何构造统计量
- 如何评价统计量
- 常用的点估计方法:
- [[参数估计#矩估计法|矩估计法]]
- [[参数估计#极大似然估计法|极大似然估计法]]
#概率论重点 矩估计法
- 设\((X_1,X_2,...,X_n)\)为来自总体\(X\)的一个样本,且\(E(E^r)=\mu_r\),则\(\lim _{n \rightarrow \infty} \frac{1}{n} \sum_{i=1}^{n} X_{i}^{r} \stackrel{P}{=} \mu_{r}=E\left(X^{r}\right)\)
- 当n充分大时,有\(\frac{1}{n} \sum_{i=1}^{n} X_{i}^{r} \approx E\left(X^{r}\right)\)
- 原理:大数定律
- 定义:用样本\((X_1,X_2,...,X_n)\)的\(r\)阶原点矩\(A_{r}= \frac{1}{n}\sum _{i=1}^{n}X_{i}^{r}\)作为总体\(X\)的\(r\)阶原点矩\(E(X^r)\)的估计量
- 所产生的的参数估计方法称为矩估计法
- 由矩估计法得到的估计量叫做矩估计量
[!思想与方法] 用样本矩代替理论矩,依照低阶矩有限原则,建立k个方程,从中接触k个未知参数的矩估计量
- 当\(k=1\)时
- 如果\(E(X)\)中含有未知参数\(\theta\),则建立方程\(\bar X = E(X)\),解出\(\hat \theta\)
- 如果不含,则根据低阶矩优先原则,进一步建立二阶原点矩方程\(\frac{1}{n} \sum_{i=1}^{n} X_{i}^{2}=E\left(X^{2}\right)\)
- 如果仍不含,则继续使用三阶
[!注] “\(=\)”为形式上的几号,实质上应该为"\(\approx\)" 因此由此解出的\(\theta\)是估计量,并非精确值,则称为估计值\(\hat \theta\)
- 如果仍不含,则继续使用三阶
- 如果不含,则根据低阶矩优先原则,进一步建立二阶原点矩方程\(\frac{1}{n} \sum_{i=1}^{n} X_{i}^{2}=E\left(X^{2}\right)\)
- 如果\(E(X)\)中含有未知参数\(\theta\),则建立方程\(\bar X = E(X)\),解出\(\hat \theta\)
- 当\(k=2\)时
- 如果\(E(X)\)和\(E(X^2)\)中含有未知参数\(\theta_1\)和\(\theta_2\),则建立方程组\(\left\{\begin{array}{l}\bar{X}=E X \\ \frac{1}{n} \sum_{i=1}^{n} X_{i}^{2}=E\left(X^{2}\right)\end{array}\right.\),进而得解
- 例:

- 直观意义:用n次观察的平均次数近似代替一般情况下,该电话再次时间段内的平均呼唤次数



#概率论重点 极大似然估计法
[!Fisher的极大似然思想] 随机试验有多个可能的结果,但在一次试验中,有且只有一个结果会出现 如果在某次实验中,结果\(\omega\)出现了,则认为该结果(事件\(\{\omega\}\))发生的概率\(P\{\omega\}\)最大 - 似然函数:设\(X_1,X_2,...,X_n\)是来自总体\(X\)的样本,\(x_1,x_2,...,x_n\)是样本观测值,则\(L(\theta)\)为似然函数 - 离散型:\(L(\theta)=L(\theta ;x_{1},x_{2}, \cdots ,x_{n})= \prod _{i=1}^{n}P \left\{ X_{i}=x_{i}\right\} , \theta \in \theta\) - 连续型:\(L(\theta)=L(\theta ;x_{1},x_{2}, \cdots ,x_{n})= \prod _{i=1}^{n}f(x_{i}; \theta), \theta \in \theta\) - 极大似然估计量:设\(X_1,X_2,...,X_n\)是来自总体\(X\)的样本,\(x_1,x_2,...,x_n\)是样本观测值,\(L(\theta)\)为似然函数,若存在统计量\(\hat{\theta}=\hat{\theta}\left(x_{1}, x_{2}, \cdots, x_{n}\right)\)使得\(L(\hat{\theta})=\sup _{\theta \in \Theta} L(\theta)\),则称\(\hat{\theta}\)为极大似然估计量
-
概率论重点 极大似然估计量的求解方法与步骤
- 写出似然函数\(L(\theta)\)
- 取对数\(\ln{L(\theta)}\),令\(\frac{d \ln L(\theta)}{d \theta}=0 \quad(k = 1)\)或\(\frac{\partial \ln L(\theta)}{\partial \theta_{i}}=0\quad i=1,2(k=2)\)
- 若从中解得唯一驻点\(\hat\theta\),或\(\hat\theta = (\hat{\theta_1},\hat{\theta_2})\),则\(\hat\theta\)为\(\theta\)的极大似然估计值
- 如果上述方程无解,则通过\(L(\theta)\)的单调性进行讨论,在某边界点求出\(\theta\)或\(({\theta_1},{\theta_2})\)的极大似然估计量
- 例
估计量的评价标准
#概率论重点 无偏性
- 设\(\hat\theta\)为\(\theta\)的估计量,如果对任意的\(\theta\in\Theta\),均有\(E(\hat\theta)=\theta\),则称\(\hat\theta\)为无偏估计,否则,为有偏估计
- 如果\(\lim_{n\to \infty}E(\hat\theta)=\theta\),则称\(\hat\theta\)为\(\theta\)的渐进无偏估计
[!无偏估计的直观意义] 由于样本\((X_1,X_2,...,X_n)\)是随机的,估计\(\theta\)时,有时偏高有时偏低,总体平均是等于\(\theta\)的,因此,讨论无偏性的关键在于计算\(E(\hat\theta)\)
- 如果\(\lim_{n\to \infty}E(\hat\theta)=\theta\),则称\(\hat\theta\)为\(\theta\)的渐进无偏估计
- 定理:设总体\(X\)的数学期望\(E(X)=\mu\),方差\(DX=\sigma^2\),\((X_1,X_2,...,X_n)\)为来自总体\(X\)的样本
- \(\bar X\)是\(\mu\)的无偏估计
- \(S^2\)是\(\sigma^2\)的无偏估计
- 若估计量\(\widehat{\theta}_{1}, \widehat{\theta}_{2}, \cdots \widehat{\theta}_{m}\)均为\(\theta\)的无偏估计,\(c_{1},c_{2}, \cdots ,c_{m}\)为常数,且\(\sum_{i=1}^mc_i=1\),则\(\sum_{i=1}^mc_i\hat\theta=1\)仍然为\(\theta\)的无偏估计
- 例: