数理统计的基础知识
数理统计的基本概念
- 数理统计就是一个归纳推断的过程
- 数理统计是以概率论为基础,关于试验数据的收集、整理、分析、推断的科学和艺术
- 试验数据:科学试验或对某事物、现象进行观察获得的数据称为试验数据
- 特点:数据受随机因素的影响,我们可以通过某种概率分布来描述
总体和样本
- 总体与个体:
- 总体:研究问题中所有被考察对象的全体
- 个体:总体中的每个成员
[!注] 由于被考察对象往往是某数量指标\(X\),因此总体可以理解为该数量指标\(X\)的全体,而在实际问题中,数量指标\(X\)可以理解为一个随机变量 随机变量X的分布称为总体的分布,总体的特征是由总体的分布刻画的,因此,常把总体与总体分布视为等同,并称总体\(X**\)
 **如果从总体中随机抽取一个个体,则该个体也为随机变量,且与总体同分布
**如果从总体中随机抽取一个个体,则该个体也为随机变量,且与总体同分布
-
样本:
- 从总体\(X\)中,按一定的规则任意抽取的部分个体\((X_1,X_2,...,X_n)\)称为来自总体\(X\)的一个样本
- \(n\)为样本容量或样本大小
- 样本可以称为\(n\)维随机变量
- 简单随机样本(在书里统计中,要求所有样本都是简单随机样本):
- 代表性:与总体同分布
- 独立性:每一个样本个体之间相互独立
由部分推到总体中的部分即样本,后续对总体的研究都是通过样本进行的
- 从总体\(X\)中,按一定的规则任意抽取的部分个体\((X_1,X_2,...,X_n)\)称为来自总体\(X\)的一个样本
-
样本的分布:
- 离散型:
- 总体\(X\)的分布律:\(P \left\{ X=a_{i}\right\} =p(a_{i}),i=1,2,\cdots\)
- 则样本的分布律:\(P \left\{ X_{1}=x_{1},X_{2}=x_{2}, \cdots ,X_{n}=x_{n}\right\} =P \left\{ X_{1}=x_{1}\right\} P \left\{ X_{2}=x_{2}\right\} \cdots P \left\{ X_{n}=x_{n}\right\}=p(x_{1})p(x_{2})\cdots p(x_{n})= \prod _{i=1}^{n}p(x_{i})\)
- 连续型:\(f(x),- \infty <x<+\infty\)
- 总体X的分布律:\(f(x),- \infty <x<+\infty\)
- 则样本的分布律:\(f(x_{1},x_{2}, \cdots ,x_{n})=f_{x_{1}}(x_{1})f_{x_{2}}(x_{2})\cdots f_{x_{n}}(x_{n})=f(x_{1})f(x_{2})\cdots f(x_{n})= \prod _{i=1}^{n}f(x_{i})\)
- 离散型:
- 样本的二重性:
- 抽样之前或理论研究时:样本\((X_1,X_2,...,X_n)\)为n维随机变量
- 抽样后或实际应用时:在具体的一次观测或试验中,得到样本的一组数据,称为样本的观察值或样本值(具体)
- 将观察值记为:\((x_1,x_2,...,x_n)\)

- 将观察值记为:\((x_1,x_2,...,x_n)\)
统计量
- 统计量:
- 设\((X_1,X_2,...,X_n)\)为来自总体\(X\)的样本,\(g(x_1,x_2,...,x_n)\)为一个n元函数,且\(g(x_1,x_2,...,x_n)\)不依赖总体\(X\)中的任何未知参数,则称随机变量\(g(x_1,x_2,...,x_n)\)为一个统计量

- 同时,称\(g(x_1,x_2,...,x_n)\)为统计量的观察值
[!NOTE] 统计量是样本的函数,而在实际问题中,统计量表现为处理统计问题的方法。不同的统计量表示不同的处理方法,好的统计量表示好的处理方法 例如: - 在比较两个平行班的教学的数学测验成绩中,通常采用取平均值的方法进行比较,构造的统计量为\(\frac{1}{n}\sum_{i=1}^nX_i\) - 在数学竞赛中,采用统计量\(\max_{1\le i \le n}X_i\)
- 同时,称\(g(x_1,x_2,...,x_n)\)为统计量的观察值
- 设\((X_1,X_2,...,X_n)\)为来自总体\(X\)的样本,\(g(x_1,x_2,...,x_n)\)为一个n元函数,且\(g(x_1,x_2,...,x_n)\)不依赖总体\(X\)中的任何未知参数,则称随机变量\(g(x_1,x_2,...,x_n)\)为一个统计量
- 常见的统计量:
- 样本矩
- 样本均值:\(\overline{X}= \frac{1}{n}\sum _{i=1}^{n}X_{i}\)
- 样本方差:\(S^{2}= \frac{1}{n-1}\sum _{i=1}^{n}(X_{i}- \overline{X})^{2}= \frac{1}{n-1}(\sum _{i=1}^{n}X_{i}^{2}-n \overline{X}^{2})\)
- 样本标准差:\(S= \sqrt{S^{2}}\)
- 样本k阶原点矩:\(A_{k}= \frac{1}{n}\sum _{i=1}^{n}X_{i}^{k},k=1,2,\cdots\)
- 样本k阶中心距:\(B_{k}= \frac{1}{n}\sum _{i=1}^{n}(X_{i}- \overline{X})^{k},k=1,2,\cdots\)
-
概率论重点 设总体\(X\)的数学期望\(E(X)=\mu\),方差\(D(X)=\sigma^2\),\((X_1,X_2,...,X_n)\)为来自总体\(X\)的一个样本,则
- \(E(\bar X)=\mu\)
- \(D(\bar X)=\frac{\sigma^2}{n}\)
- \(E(S^2)=\sigma^2\)
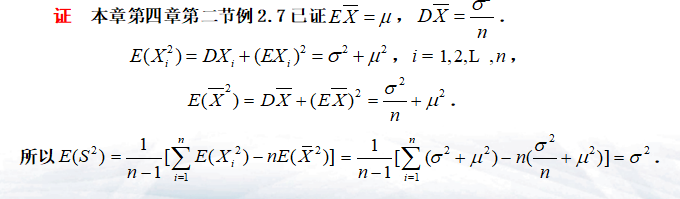
- 顺序统计量:设\((X_1,X_2,...,X_n)\)为来自样本\(X\)的样本,将其排序为\(X_{1}^{*}\leq X_{2}^{*}\leq \cdots \leq X_{n}^{*}\),则称\(X_{1}^{*},X_{2}^{*}, \cdots ,X_{n}^{*}\)为顺序统计量
- \(X_{1}^{*}= \min \left\{ X_{1},X_{2}, \cdots ,X_{n}\right\} ,X_{n}^{*}= \max \left\{ X_{1},X_{2}, \cdots ,X_{n}\right\}\)
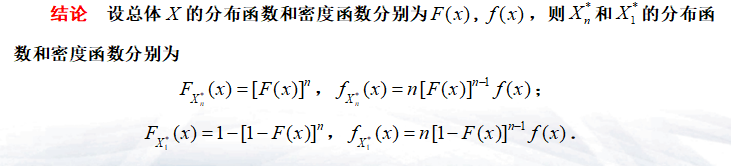
- \(X_{1}^{*}= \min \left\{ X_{1},X_{2}, \cdots ,X_{n}\right\} ,X_{n}^{*}= \max \left\{ X_{1},X_{2}, \cdots ,X_{n}\right\}\)
- 样本矩
抽样分布
- 统计量的分布称为抽样分布
统计中的常见分布
正态分布
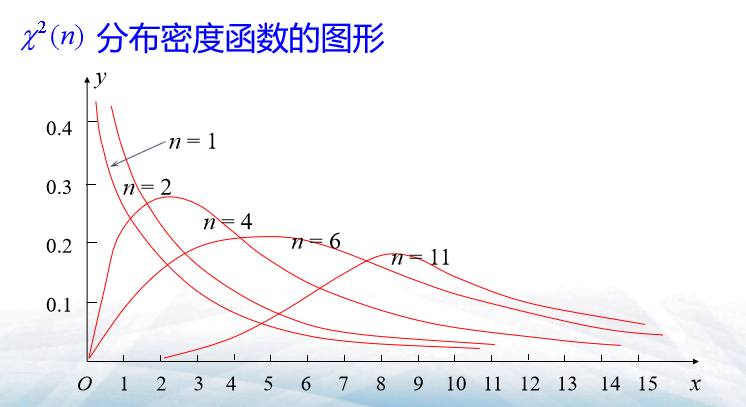
\(\mathcal{X}^2\)分布
- 设\((X_1,X_2,...,X_n)\)为来自总体\(X\sim N(0,1)\)(标准正态分布)的一个样本,就称统计量\(\mathcal{X}^2=\sum_{i=1}^{n}X_i^2\)为服从自由度为n的\(\mathcal{X}^2\)分布
- 记作\(\mathcal{X}^2\sim \mathcal{X}^2(n)\)
- 通俗的讲:\(\mathcal{X}^2(n)\)是由n个相互独立的标准正态随机变量的平方和组成
- 设\(\mathcal{X}^2\sim \mathcal{X}^2(n)\),则\(\mathcal{X}^2\)的密度函数:\(f(x,n)= \left\{ \begin{matrix} \frac{1}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}x^{\frac{n}{2}-1}e^{- \frac{x}{2}}, \quad x>0, \\ 0, \quad x \leq 0, \\ \end{matrix} \right.\)
- 其中\(\Gamma(p)= \int _{0}^{+ \infty}x^{p-1}e^{-x}dx(p>0)\)称为\(\Gamma\)函数
- 密度函数的图形:
- 性质:
- \(\mathcal{X}^2\sim \mathcal{X}^2(n)\),则\(E(\mathcal{X}^2)=n\quad D(\mathcal{X}^2)=2n\)
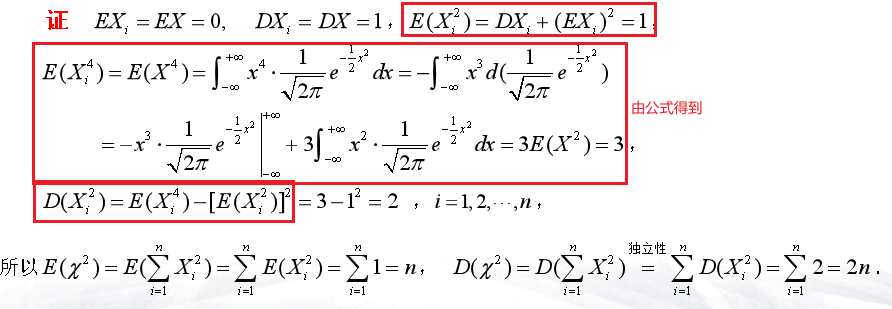
- 设\(X\sim N(0,1)\),则\(X^2\sim \mathcal{X}^2(1)\)
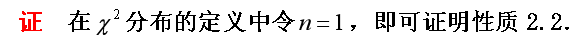
- 设\(\mathcal{X}_i^2 \sim \mathcal{X}^2(n_i),i=1,2\),且\(\mathcal{X}_{1}^{2}, \mathcal{X} _{2}^{2}\)相互独立,则\(\mathcal{X}_1^2+\mathcal{X}_2^2\sim \mathcal{X}^2(n_1,n_2)\)
- 推论:\(\sum_{i=1}^{k}\mathcal{X}_i^2\sim \mathcal{X}^2(\sum_{i=1}^{k}n_i)\)(前提:相互独立)
- \(\mathcal{X}^2\sim \mathcal{X}^2(n)\),则\(E(\mathcal{X}^2)=n\quad D(\mathcal{X}^2)=2n\)
t分布
- 设随机变量\(X\sim N(0,1),Y\sim\mathcal{X}^2(n)\),且\(X\)与\(Y\)相互独立,则称\(T=\frac{X}{\sqrt{\frac{Y}{n}}}\)服从自由度为n的t分布
- 记作\(T\sim t(n)\)
- \(T\sim t(n)\)的密度函数:\(f(x_{1}n)= \frac{\Gamma(\frac{n+1}{2})}{\sqrt{n \pi}\Gamma(\frac{n}{2})}(1+ \frac{x^{2}}{n})^{- \frac{n+1}{2}},- \infty <x<+ \infty .\)

F分布
- 设随机变量\(X \sim \chi ^{2}(n_{1}),Y \sim \chi ^{2}(n_{2})\),且\(X\)与\(Y\)相互独立,则称\(F=\frac{\frac{X}{n_1}}{\frac{Y}{n_2}}\)为服从第一自由度为\(n_1\),第二自由度为\(n_2\)的\(F\)分布
- 记作\(F\sim F(n_1,n_2)\)
- \(F\sim F(n_1,n_2)\)的密度函数:\(f\left(x ; n_{1}, n_{2}\right)=\left\{\begin{array}{ll}\frac{\Gamma\left(\frac{n_{1}+n_{2}}{2}\right)}{\Gamma\left(\frac{n_{1}}{2}\right) \Gamma\left(\frac{n_{2}}{2}\right)} n_{1}^{\frac{n_{1}}{2} n_{2}} \frac{n_{2}}{2} x^{\frac{n_{1}}{2}-1}\left(n_{1} x+n_{2}\right)^{-\frac{n_{1}+n_{2}}{2}}, & x>0 \\0, & x \leq 0\end{array}\right.\)
- 性质:
- \(T\sim t(n) \rightarrow T^2\sim F(1,n)\)
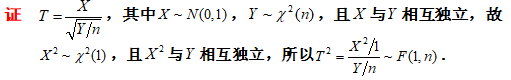
- \(F \sim F(n_{1},n_{2})\rightarrow \frac{1}{F}\sim F(n_{2},n_{1})\)
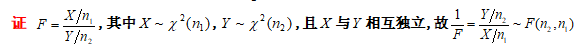
- \(T\sim t(n) \rightarrow T^2\sim F(1,n)\)
上侧分位点
- 设\(X\)为随机变量,\(p\)为满足\(0 < p < 1\)的实数,如果点\(x_p\)满足\(P \left\{ X \geq x_{p}\right\} \geq p,P \left\{ X \leq x_{p}\right\} \geq 1-p\),则称\(x_p\)为\(X\)的上侧\(p\)分位点或右侧\(p\)分位点
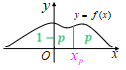
- 对于正态分布,\(\mathcal{X}^2\)分布,\(t\)分布和\(F\)分布,其上侧分位点均唯一存在
- 并且对于上述分布,其下标\(p\)表示该点右侧的面积
- 标准正态分布\(N(0,1)\)的上侧分位点
- \(P\{U \ge U_\alpha\}=\alpha\)
- 利用正态分布的对称性,\(U_{1-\alpha}=-U_\alpha\)
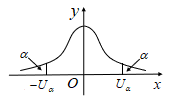
- \(P\{U\ge U_\alpha\}=\alpha\)等价于\(\Theta(U_\alpha)=1-\alpha\)
- \(U_\alpha\)可以通过标准正态分布表查得

- t分布\(t(n)\)的上侧分位点
- \(P \left\{ T \geq t_{\alpha}(n)\right\} =\alpha\)
- 利用t分布的对称性:\(t_{1- \alpha}(n)=-t_{\alpha}(n)\)
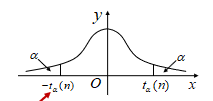
- \(t_\alpha(n)\)可以通过查找t分布表得到
- \(\mathcal{X}^2\)分布\(\mathcal{X}^2(n)\)的上侧分位点
- \(P \left\{ \chi ^{2}\geq \chi _{\alpha}^{2}(n)\right\} =\alpha\)
- 由于\(\mathcal{X}^2\)分布的非对称性:\(P\{\mathcal{X}^2\ge \mathcal{X}_{1-\alpha}^2(n)\}=1-\alpha\)即\(P\{\mathcal{X}^2\le \mathcal{X}_{1-\alpha}^2(n)\}=\alpha\)
- 通过分布表查得
- \(F\)分布\(F(n_1,n_2)\)的上侧分位点
- \(P \left\{ F \geq F_{\alpha}(n_{1},n_{2})\right\} =\alpha\)
- 由于F分布的非对称性:\(P \left\{ F \geq F_{1- \alpha}(n_{1},n_{2})\right\} =1-\alpha\)
- 不能直接通过分布表查得,需要利用性质\(F_{1- \alpha}(n_{1},n_{2})= \frac{1}{F_{\alpha}(n_{2},n_{1})}\)转换后得到
正态总体样本均值和样本方差的分布
单正态总体样本均值和样本方差的分布
- 设\((X_1,X_2,...,X_n)\)为来自总体\(X\sim N(\mu, \sigma^2)\)的一个样本,则
- \(\overline{X}\sim N(\mu , \frac{\sigma ^{2}}{n})\)或\(U= \frac{\overline{X}- \mu}{\sigma / \sqrt{n}}\sim N(0,1)\)
- \(T= \frac{\overline{X}- \mu}{S/ \sqrt{n}}\sim t(n-1)\)
- \(\chi ^{2}= \frac{\sum _{i=1}^{n}(X_{i}- \mu)^{2}}{\sigma ^{2}}\sim \chi ^{2}(n)\)
- \(\mathcal{X} ^ { 2 } = \frac { ( n - 1 )S ^ { 2 } } { \sigma ^ { 2 } } = \frac { \sum _ { i = 1 } ^ { n } ( X _ { i } - \bar X ) ^ { 2 } } { \sigma ^ { 2 } } \sim \mathcal{X}^ { 2 } ( n - 1 )\),且\(\bar X\)与\(S^2\)相互独立

