随机事件及其概论

随机试验与随机事件

• 自然界与社会生活中的两类现象
  • 确定性现象：结果确定
  • 不确定性现象：结果不确定

随机试验

• 随机试验\(E\):
  • 满足：
    • 重复性：在相同条件下，实验可重复进行
    • 明确性：试验的所有可能结果均实现已知
    • 随机性：每次试验的具体结果在试验前无法预知

样本点、样本空间和随机事件

• 样本点\(\omega\)：随机试验\(E\)的每一个可能出现的基本结果
• 样本空间\(\Omega\)：随机试验\(E\)的所有样本点的全体
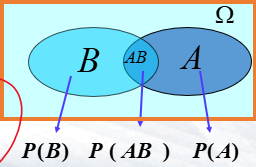
• 样本点的集合为随机事件，简称为事件，记为\(A、B、C\)等
  • 由一个样本点构成的单点集称为基本事件
  • 随机事件是样本空间\(\Omega\)的子集
  • 当随机试验\(E\)中所出现的样本点\(\omega \in A\)时，称事件A发生，当\(\omega \notin A\)时，称A不发生

    必然事件：每次试验中，必然发生的事件，从集合角度看，必然事件为全集，即样本空间\(\Omega\) 不可能事件：每次试验中，不可能发生的事件称为不可能事件，从集合角度看，不可能事件为空集\(\varnothing\)

事件间的关系及其运算

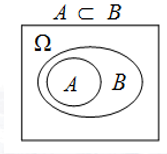
• 包含：
  • 如果A发生，则B一定发生
  • \(A \subset B\)
  • 
• 事件的相等
  • 事件A、B互相包含（\(A\subset B、B\subset A\)）
  • \(A=B\)
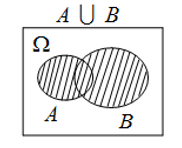
• 并事件
  • 事件A、B中至少发生一个
  • \(A \cup B\)
  • 
• 交事件
  • 事件A、B都发生
  • \(A\cap B\)
  • 
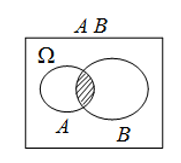
• 差事件
  • A发生且B不发生
  • \(A-B=A-AB\)
  • 
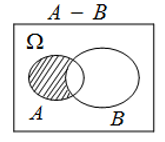
• 互不相容事件
  • 事件AB不可能都发生
  • \(AB=\varnothing\)
  • 
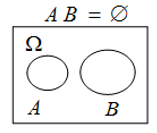
• 对立事件
  • \(A\cup B = \Omega、AB=\varnothing\)
• 事件的运算律

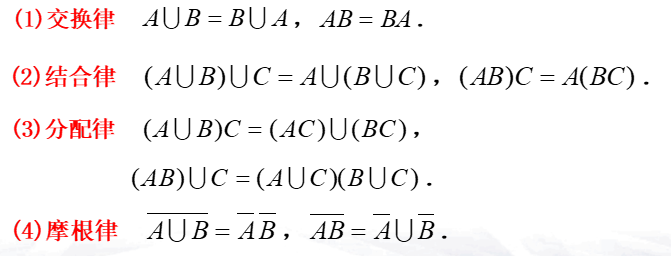
概率及其性质

概率的定义

• 三种定义方式：
  • 概率的描述性定义：从实际意义上讲，随机事件\(A\)的概率\(P(A)\)为\([0,1]\)上的一个数值，该数值体现了随机事件\(A\)发生的可能性的大小
  • 概率的统计定义：
    • 
  • 概率的公理化定义：

概率的性质

• 非负性
• 规范性
• 有限可加性

• 概率论重点 差事件概率计算公式：\(P(A-B)=P(A)-P(AB)=P(A\bar{B})\)

  • 当\(B\subset A\)，有\(P(A-B)=P(A)-P(B)\)
• 对立事件概率计算
• 并事件概率计算公式：\(P(A\cup B) = P(A)+P(B)-P(AB)\)
  • \(P(A\cup B\cup C) = P(A)+P(B)+P(C) - P(AB) - P(AC) - P(BC) + P(ABC)\)

古典概型与几何概型

古典概型

• 古典概型试验（等可能概型试验）：
  • 随机试验E的样本空间\(\Omega\)中只有有限个样本点
  • 每次试验中各基本事件出现的概率相等
• \(P(A)=\frac{m}{n}=\frac{事件A所含样本点的个数}{所有样本点的个数}\)
• 关键：分子与分母的计数
• 通常需要用排列与组合
  • 排列：从n个不同的元素中，任取k个元素按次序排列，称为从n个元素中任取k个元素的排列
    • 不可重复：\(A^{k}_{n}=\frac{n!}{(n-k)!}\)
    • 可重复：\(n^k\)
  • 组合：从n个不同的元素中，任取k个不重复元素组成一个子集（不考虑元素的次序），称为从n个元素中任取k个元素的组合
    • \(C^k_n=\frac{n!}{k!(n-k)!}\)

几何概型

• 几何概型试验：
  • 随机试验E的样本空间\(\Omega\)为某几何区域
  • 每次试验中各基本事件出现的机会相等
• \(P(A)=\frac{A的几何测度}{\Omega的几何测度}\)

  几何测度：根据样本空间\(\Omega\)是一维区域或二位区域分别为长度或面积

条件概率与乘法公式

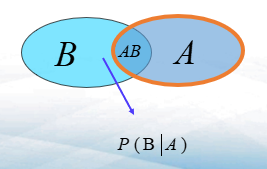
条件概率

• 在已知事件A发生的条件下，事件B发生的概率称为条件概率，记为\(P(B|A)\)
• \(P(B|A)=\frac{S(AB)}{S(A)}=\frac{\frac{S(AB)}{S(\Omega)}}{\frac{S(A)}{S(\Omega)}}=\frac{P(AB)}{P(A)}\)
• 性质：
  • 非负性：\(0 \le P(B|A) \le 1\)
  • 规范性：\(P(\Omega|A)=1\)
  • 可列可加性：
    • 设事件\(B_1,B_2...B_n\)两两互不相容，则\(P(B_1\cup B_2\cup ... \cup B_n \cup ...|A) = P(B_1|A)+P(B_2|A)+...+P(B_n|A)+...\)
• 计算方法：

  • 概率论重点 公式法：\(P(B|A)=\frac{P(AB)}{P(A)}\)

  • 融入法：在条件概率空间中直接计算
  • 

乘法公式

• 设\(P(A)>0\)，则\(P(AB)=P(A)P(B|A)\)
  • 其中的条件概率\(P(B|A)\)是由融入法计算或直接提供
• 一般来说，如果随机试验\(E\)具有链式结构特征，则适合应用乘法公式计算有关事件的概率
  • \(P(A_1A_2...A_n)=P(A_1)P(A_2|A_1)P(A_3|A_1A_2)...P(A_n|A_1A_2...A_{n-1})\)
    • \(P(A_1A_2A_3)=P(A_1)P(A_2|A_1)P(A_3|A_1A_2)\)

      链式结构特征：试验的过程一环扣一环

全概率公式和贝叶斯公式

#概率论重点 全概率公式

• 完备事件组：如果事件组\(A_1,A_2,...,A_n,...\)两两互不相容，且\(A_1 \cup A_2 \cup ... \cup A_n \cup ... = \Omega\)，则称事件组\(A_1,A_2,...,A_n,...\)构成样本空间\(\Omega\)的一个完备事件组
  • 
• 全概率公式（由因求果）：
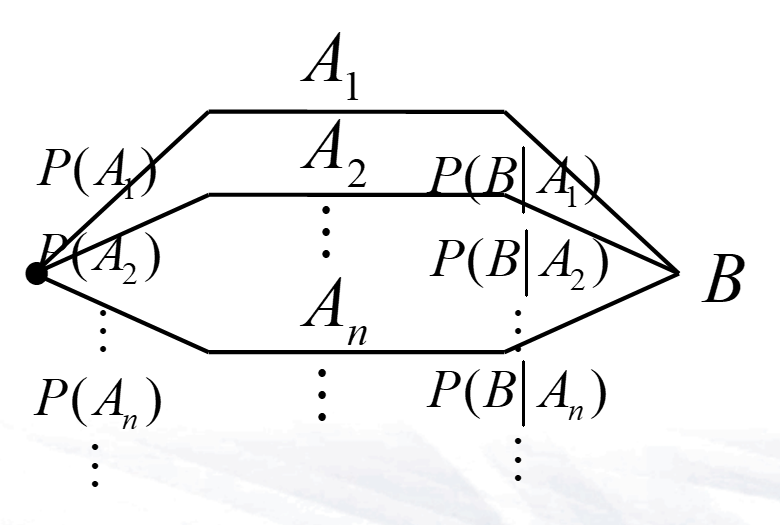
  • 设事件组\(A_1,A_2,...,A_n,...\)为样本空间\(\Omega\)的一个完备事件组，且\(P(A_i)>0\)，则对任何事件B有\(P(B)=\sum^{\infty}_{i=1}P(A_i)P(B|A_i)\)
  • 
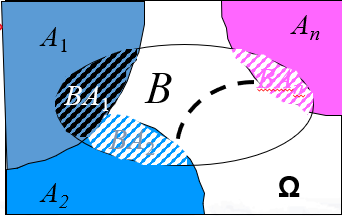
  • 当随机试验E的过程具有并列结构特征，适合应用全概率公式计算有关事件的概率
  • 当完备事件组为\(A\)和\(\bar A\)时，全概率公式为\(P(B)=P(A)P(B|A)+P(\bar A)P(B|\bar A)\)

贝叶斯公式

• 贝叶斯公式（由果求因->逆概率公式）：设事件组\(A_1,A_2,...,A_n,...\)为样本空间\(\Omega\)的一个完备事件组，\(B\)为一随机事件，则\(P(A_j|B)=\frac{P(A_j)P(B|A_j)}{P(B)}\)
  • 证明：\(P(A_j|B)=\frac{P(A_jB)}{P(B)}=\frac{P(A_j)P(B|A_j)}{P(B)}\)
  • 同样可以写作：\(P(A_j|B)=\frac{P(A_j)P(B|A_j)}{\sum^{\infty}_{0}P(A_i)P(B|A_i)}\)
  • 简单表示：\(后验概率 = \frac{先验概率 \times 可能性}{全部可能}\)
• 贝叶斯公式的解题步骤：
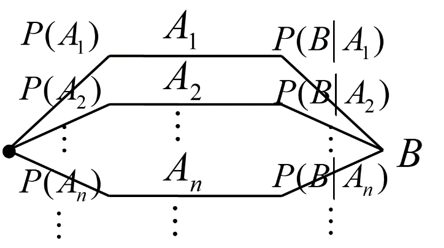
  1. 使用全概率公式求出\(P(B)=\sum^{\infty}_{0}P(A_i)P(B|A_i)\)
  2. 将图中第j行的左右两个概率相乘得\(P(A_j)P(B|A_j)\)
  3. 计算\(P(A_j|B)=\frac{P(A_j)P(B|A_j)}{P(B)}\)
• eg：

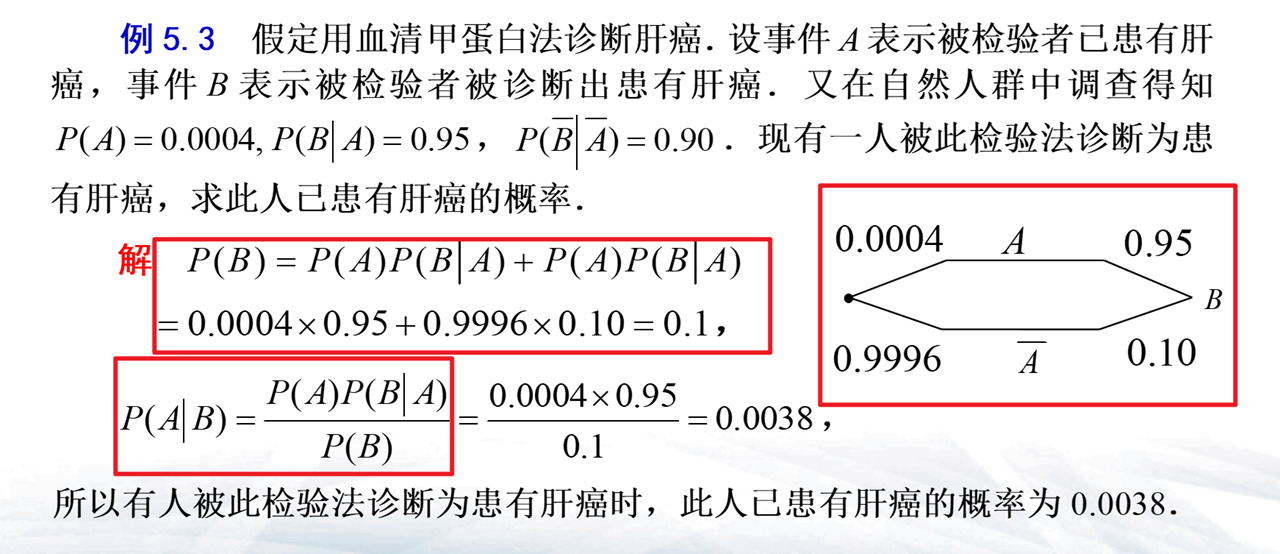
事件的独立性与伯努利概型

事件的独立性

• 事件独立：\(P(B|A)=P(B)\)或\(P(AB)=P(A)P(B)\)
  • 事件A的发生对事件B发生的可能性并无影响
  • 直观理解：事件A、B各自发生与否没有关系

    [!注] 事件相互独立和事件 互不相容是两个不同的概念 如果事件A和B互相独立，且A和B不可能互不相容，则\(0=P(AB)=P(A)P(B)\) 则\(P(A)=0\)或\(P(B)=0\)，为零概率事件

• 设\(P(A)>0\)，则事件A、B互相独立的充要条件为\(P(B|A)=P(B)\)
• 设A、B为两个随机事件，则下列四对事件相互独立是等价的
  • \(A,B\)
  • \(A,\bar B\)
  • \(\bar A,B\)
  • \(\bar A,\bar B\)
• 

三个事件的独立性

• 如果：\(\(\begin{cases}P(AB)=P(A)P(B)\\P(AC)=P(A)P(C)\\P(BC)=P(B)P(C)\end{cases}\)\)则称随机事件A、B、C两两独立
• 两两独立\(\neq\)三者之间独立
• 若随机事件A、B、C两两独立，且\(P(ABC)=P(A)P(B)P(C)\)，则称事件A、B、C相互独立
  • 若随机事件\(A_1,A_2,...,A_n,...\)满足\(P(A_1A_2...A_n...)=P(A_1)P(A_2)...P(A_n)...\)，则随机事件\(A_1,A_2,...,A_n,...\)相互独立
    • 则\(A_1,A_2,...,A_n,...\)任意不分时间相互独立（至少两个事件）
    • 则分别将\(A_i\)不变或换为\(\bar{A_i}\)后的事件仍相互独立
      • 
    • 如果随机事件\(A_1,A_2,...,A_n,...,B_1,B_2,...,B_n,...\)相互独立，则由\(A_1,A_2,...,A_n,...\)组成的事件与由\(B_1,B_2,...,B_n,...\)组成的事件相互独立
      • 

伯努利概型

• n重独立重复实验：
  • 试验E重复进行n次
  • 每次试验对应的样本空间相同
  • 各次试验结果相互独立
• 若每次试验仅有两种结果（\(A、\bar A\)），则称之为n重伯努利试验
• 在n重伯努利试验中，事件A恰好发生k次的概率为：\(C^k_n p^k(1-p)^{n-k}\)