跳转至

随机变量的数字特征

数学期望

数学期望的概念

  • 随机变量的数学期望也被称为随机变量的均值，体现了随机变量的一种平均取值

离散型随机变量的数学期望

\[X \sim \left( \begin{array} { l l l } { x _ { 1 } } & {x_2}&{ \cdots } & { x _ { i } } & { \cdots } \\ { p _ { 1 } } & { p _ { 2 } } & { \cdots } & {p_n} & {\cdots} \end{array} \right)\]
  • 如果无穷级数\(\sum^{\infty}_{i=1}x_ip_i\)绝对收敛，则称之为X的数学期望或均值，记作\(E(X)\)或\(EX\) (\(E(X)=\sum^{\infty}_{i=1}x_ip_i\)\)

    [!注] 1. 这里所计算的期望值为加权平均值 2. 绝对收敛保证了期望与求和的次序无关 3. 若无穷级数\(\sum^{\infty}_{i=1}x_ip_i\)不绝对收敛，则不存在数学期望

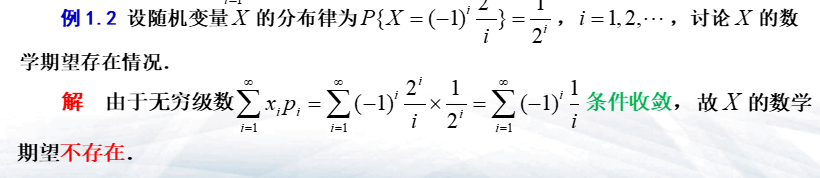
连续型随机变量的数学期望

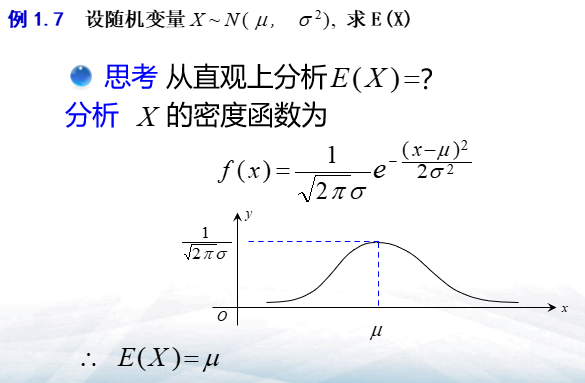
  • 设随机变量\(X\)的密度函数为\(f(x)\)，如果广义积分\(\int_{-\infty}^{+\infty}xf(x)\)绝对收敛，则称之为X的数学期望或均值，记作\(EX\)或\(E(X)\)，即\(\(E(X)=\int^{+\infty}_{-\infty}xf(x)dx\)\)

随机变量函数的数学期望

一维随机变量函数\(Y=g(X)\)的数学期望

  • 离散型：\(E(Y)=E(g(X))=\sum^\infty_{i=1}g(x_i)p_i\)
  • 连续型：\(E(Y)=E(g(x))=\sum^{+\infty}_{-\infty}g(x)f(x)dx\)

二维随机变量函数\(Z=g(X,Y)\)的数学期望

  • 离散型：\(E(Z)=E(g(X,Y))= \sum _{i=1}^{\infty}\sum _{j=1}^{\infty}g(x_{i},y_{j})p_{ij}\)
  • 连续型：\(E(Z)=E(g(X,Y))= \int _{- \infty}^{+ \infty}\int _{- \infty}^{+ \infty}g(x,y)f(x,y)dxdy\)

数学期望的性质

  • \(Ec=c\)
  • \(E(kX)=kE(X)\)
  • \(E(X \pm Y)=E(X) \pm E(Y)\)
  • \(E(\alpha X_1+\beta X_2) = \alpha E(X_1)+\beta E(X_2)\)
    • \(E(kX+c) = kE(X)+c\)
    • \(E(a_{1}X_{1}+ \cdots +a_{n}X_{n})=a_{1}EX_{1}+ \cdots +a_{n}EX_{n}\)
  • 若随机变量\(X\)与\(Y\)相互独立，则\(E(XY)=E(X)E(Y)\)
    • 反过来并不成立
    • 若\(X_1,X_2,...,X_n\)相互独立，则\(E(X_{1}X_{2}\cdots X_{n})=EX_{1}EX_{2}\cdots EX_{n}\)
  • 如果随机变量\(X\ge a\)(或\(X\le a\))，则\(E(X)\ge a\)(或\(E(x)\le a\))
  • \([E(XY)]^2 \le E(X^2)E(Y^2)\)

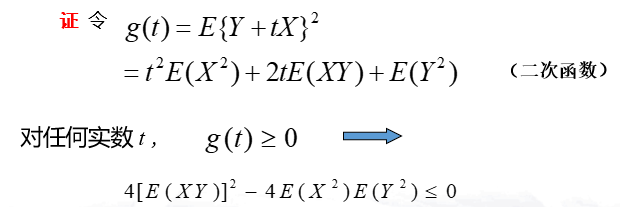
方差

方差的概念

  • 设\(X\)为随机变量，如果\(E \left[(X-E(X)^{2}\right]\)存在，则称之为X\(X\)的方差
    • 记作\(DX\)或\(D(X)\)
    • \(\sqrt{(D(X))}\)为X的标准差
    • 方差的简化计算公式（根据数学期望的性质）：\(D(X)=E(X^2)-E(X)^2\)
  • 方差的计算
    • 离散型随机变量：\(D(X)= \sum _{k=1}^{\infty}(x_{k}-E(X))^{2}\cdot p_{k}\)
    • 连续型随机变量：\(D(X)= \int _{- \infty}^{\infty}(x-E(X))^{2}\cdot f(x)dx\)

    • 概率论重点 重要计算公式：\(D(X)=E(X^2)-E(X)^2\)

方差的性质

  • \(D(c)=0\)
  • \(D(X)\ge 0\)且\(D(X)=0\)的充要条件为\(P\{X=c\}=1\)，即\(X\)服从单点分布
  • \(D(kX)=k^2D(X)\)
    • \(D(kX+c)=k^2D(X)\)
  • \(D(X\pm Y)=D(X)+D(Y)\pm 2E[((X-Y)-E(X+Y))^2]\)

    • 概率论重点 若\(X\)与\(Y\)相互独立，则\(D(X\pm Y)=D(X)+D(Y)\)

    • 若\(X_1,X_2,...,X_n\)相互独立，则\(D(a_1X_1+a_2X_2+...+a_nX_n)=a_1^2D(X_1)+a_2^2D(X_2)+...+a_n^2D(X_n)\)

#概率论重点 常见分布随机变量的数学期望和方差

\[\begin{array}{|c|c|c|c|} \hline \text { 分 布 } & \text { 分布律或概率密度 } & E X & D X \\ \hline 0 \text {-1分布 } X \sim B(1, p) & P\{X=k\}=p^{k}(1-p)^{1-k}, \quad k=0,1 . & p & p(1-p) \\ \hline \text { 二项分布 } X \sim B(n, p) & P\{X=k\}=C_{n}^{k} p^{k}(1-p)^{-k}, \quad k=0,1, \cdots, n . & n p & n p(1-p) \\ \hline \text { 泊松分布 } X \sim P(\lambda) & P\{X=k\}=\frac{\lambda^{k}}{k !} e^{-z}, \quad k=0,1,2, \cdots . & \lambda & \lambda \\ \hline \text { 几何分布 } X \sim G(p) & P\{X=k\}=(1-p)^{k-1} p, \quad k=1,2, \cdots . & \frac{1}{p} & \frac{1-p}{p^{2}} \\ \hline \text { 均匀分布 } X \sim U[a, b] & f(x)=\left\{\begin{array}{cc} \frac{1}{b-a}, \quad a \leq x \leq b, \\ 0, & \text { 其它. } \end{array}\right. & \frac{a+b}{2} & \frac{(b-a)^{2}}{12} \\ \hline \text { 指数分布 } X \sim E(\lambda) & f(x)=\left\{\begin{array}{cc} \lambda e^{-\lambda x}, & x>0, \\ 0, & x \leq 0 . \end{array}\right. & \frac{1}{\lambda} & \frac{1}{\lambda^{2}} \\ \hline \text { 正态分布 } X \sim N\left(\mu, \sigma^{2}\right) & f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}} .} & \mu & \sigma^{2} \\ \hline \end{array}\]

协方差与相关系数

协方差

  • 概念：设\((X,Y)\)为二维随机变量，如果\(E \left[(X-EY)(Y-EY)\right]\)存在，则称之为\(X\)与\(Y\)的协方差
    • 记为\(Cov(X,Y)\)，则\(Cov(X,Y)=E \left[(X-EY)(Y-EY)\right]\)
    • 协方差的简化计算公式（利用数学期望的性质）：\(Cov(X,Y)=E(XY)-E(X)E(Y)\)
  • 性质：
    • \(Cov(X,X)=DX\)
    • \(Cov(X,Y)=Cov(Y,X)\)
    • \(Cov(X,c)=0\)
    • \(Cov(aX,bY)=abCov(X,Y)\)
    • \(Cov(X_{1}\pm X_{2},Y)=Cov(X_{1},Y)\pm Cov(X_{2},Y)\)
      • \(Cov(\sum _{i=1}^{m}a_{i}X_{i}, \sum _{j=1}^{n}b_{j}Y_{j})= \sum _{i=1}^{m}\sum _{j=1}^{n}a_{i}b_{j}Cov(X_{i},Y_{j})\)
    • \(D(X \pm Y)=DX+DY \pm 2Cov(X,Y)\)
      • \(D(X \pm Y)=DX+DY \pm 2Cov(X,Y)\)
    • \(\left[ Cov(X,Y)\right] ^{2}\leq DXDY\)

      \(X\)与\(Y\)为随机变量，则下列结果等价： 1. \(X,Y\)不相关 2. \(Cov(X,Y) = 0\) 3. \(E(XY)=E(X)E(Y)\) 4. \(D(X+Y)=D(X)+D(Y)\)

  • 意义：探寻\(X,Y\)之间除了独立外的其他关系

相关系数

  • 设\((X,Y)\)为二维随机变量，如果\(DX >0,DY >0\)，则称\(\frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}\)为随机变量\(X\)与\(Y\)的相关系数
    • 记为\(\rho_{XY}\)，即\(\rho_{XY}=\frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}\)

      [!注] 可以借助向量的夹角来理解相关系数

- 独立则不相关，不相关不一定独立（\(E(X)/E(Y)=0\)）