命题逻辑
命题
命题的概念
- 命题:或真或假的陈述句
命题的分类
- 原子命题:最简单的命题
- 复合命题:多个命题通过联结词联结而成的命题
命题标识符
- 命题标识符:表示命题的符号
- 命题常量:表示确定命题的命题标识符
- 命题变量:表示任意命题位置标志的命题标识符
- 原子命题变量:任意原子命题位置标志

- 实数标识符:表示实数的符号
- 实数常量
- 实数变量

命题联结词
否定
\(\(\neg\)\)

合取
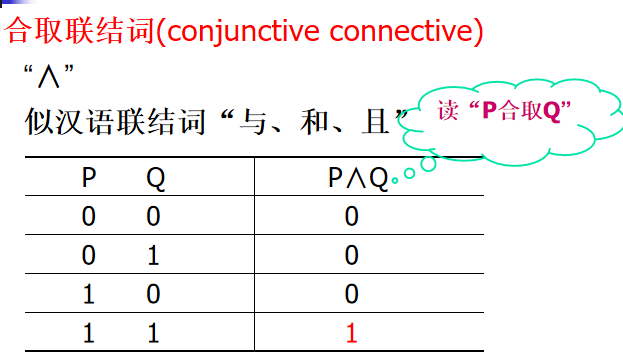
析取
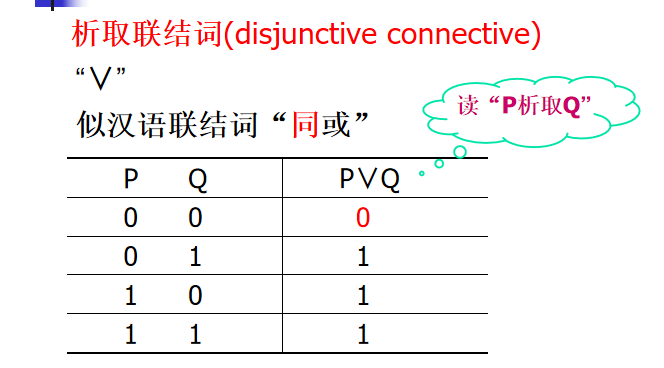
条件

双条件

混合运算
- 运算顺序:

命题公式与真值表
命题公式
- 命题公式:命题公式是由圆括号、命题变量、命题常量、联结词组成且规定了运算级的字符串
- 最外层的圆括号可以省略
- 无特别说明,字母均为命题变量
- 递归定义:

真值表
命题公式的分类
- 重言式:永真
- 矛盾式:永假
- 可满足式:可真可假
翻译
- 用数理逻辑的符号表示自然语言中的一些命题

逻辑等价
等价式
命题定律



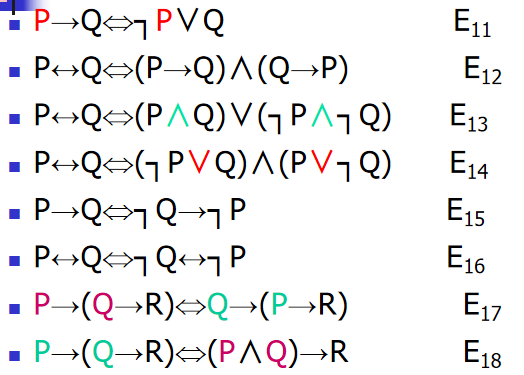
等值验算
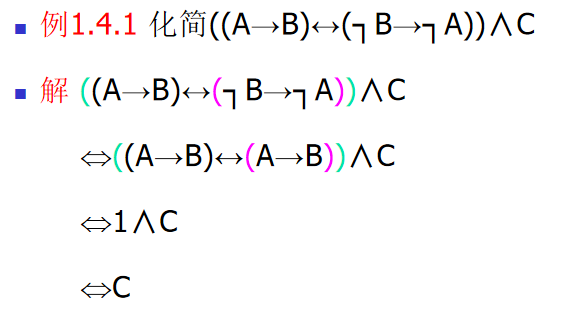

蕴含与对偶
蕴含的概念
- 蕴含:当命题公式\(P\rightarrow Q\)为重言式时,称P蕴含Q,记作\(P\Rightarrow Q\)
- 三种证明方式:
- 列真值表
- 设前件P的真值为1,证明后件Q的真值为1
- 设前件P的真值为0,证明后件Q的真值为0
蕴含定理

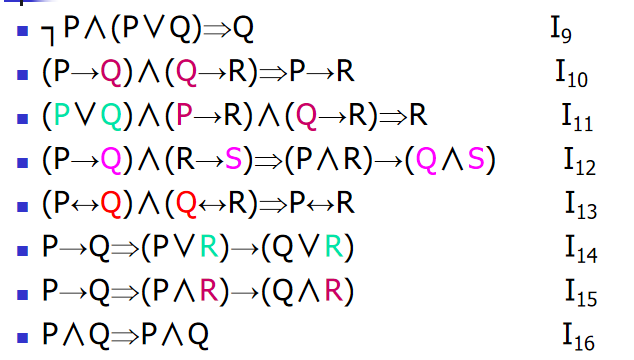
蕴含的性质
- 设命题公式A和B,\(A\Leftrightarrow B\)当且仅当\(A\Rightarrow B\)且\(B\Rightarrow A\)
- 设命题公式A和B
- 若\(A\Rightarrow B\),且A为重言式,则B为重言式
- 若\(A\Rightarrow B\)且\(B\Rightarrow C\),则\(A\Rightarrow C\)
- 若\(A\Rightarrow B\)且\(A\Rightarrow C\),则\(A\Rightarrow B\wedge C\)
- 若\(A\Rightarrow C\)且\(B\Rightarrow C\),则\(A \vee B \Rightarrow C\)
联结词的全功能集合
与非联结词
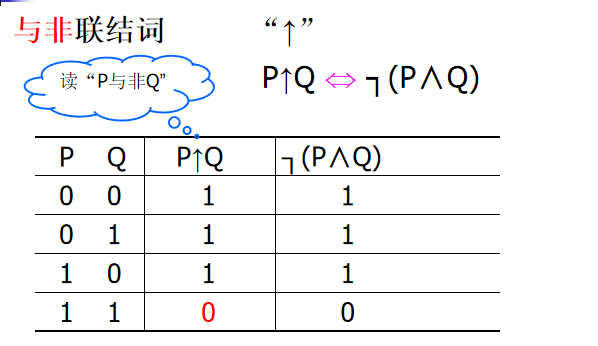
或非联结词
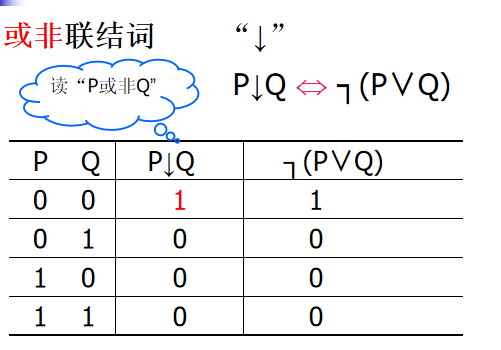
条件否定联结词
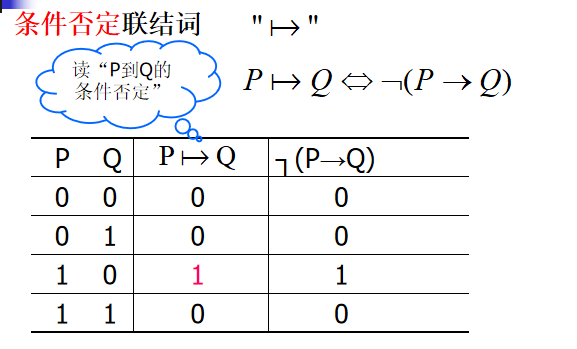
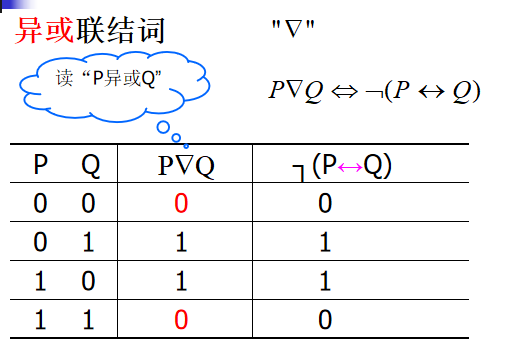
异或联结词
最小全功能集合
- 在一个命题联结词集合中,若一个联结词可由集合中其他联结词定义,则称此联结词为冗余联结词,否则称为独立联结词

- 最小全功能集合:
- 全功能集合:仅用某个联结词集合中的联结词联结的命题公式,就能表示任意命题公式
- 最小全功能集合:最小的全功能集合(不可再删)
命题逻辑的推理理论
有效推理的概念
- 若\(A_{1}\wedge A_2 \wedge ...\wedge A_n \Rightarrow B\),则称B是前提\(A_1,A_2,...,A_n\)的有效结论
- 有效推理或形式证明:

- 推理规则:前提到处有效结论的每一步都需要有正当理由
- P规则:引入前提
- T规则:蕴含定理、命题定理