群
运算及其性质
n元运算的定义


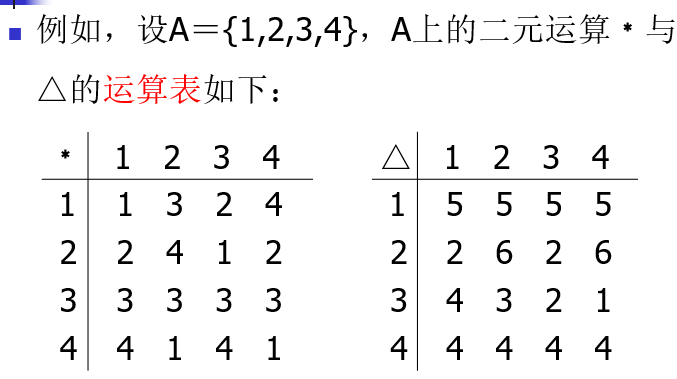
代数系统的概念


二元运算的性质
- 封闭:如果对于任意\(x,y\in A\),都有\(x*y\in A\),则称\(*\)运算在集合\(A\)上封闭,或称\(*\)运算是\(A\)上的代数运算

- \(+_m\)和\(×_m\)都是\(Z_m\)
- 交换律:\(x*y=y*x\)
- 幂等律:\(x*x=x\)
- 分配律:\(\left. \begin{array} { l } { x * ( y \Delta z ) = ( x * y ) \Delta ( x * z ) } \\ { ( y \Delta z ) * x = ( y * x ) \Delta ( z * x ) } \end{array} \right.\)
- 吸收律:\(\begin{matrix} x * ( x \Delta y ) = x \\ x \Delta ( x * y ) = x \end{matrix}\)
- 结合律:\((x*y)*z=x*(y*z)\)
半群
- 若运算\(*\)在\(A\)上结合,则称\(<A,*>\)是半群
- 设\(<A,*>\)是半群,\(B\)是\(A\)的非空子集,若\(<B,*>\)也是半群,则称\(<B,*>\)是\(<A,*>\)的子半群

幺元、零元和逆元
幺元


零元
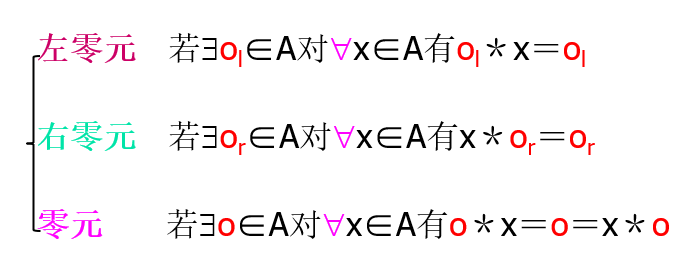

逆元


独异点
- 设\(<A,*>\)是[[群#半群|半群]],若\(A\)中有关于\(*\)运算的[[群#幺元|幺元]],则称\(<A,*>\)为独异点
- 设\(<A,*>\)是独异点,\(B\)是\(A\)的非空子集,若\(<B,*>\)也是独异点,则称\(<B,*>\)是独异点\(<A,*>\)的子独异点(submonoid)
群的基本概念
定义
- 群\(<A,*>\)
- \(<A,*>\)是[[群#独异点|独异点]]
- 结合
- 幺元
- 其中的任意元素都有逆元
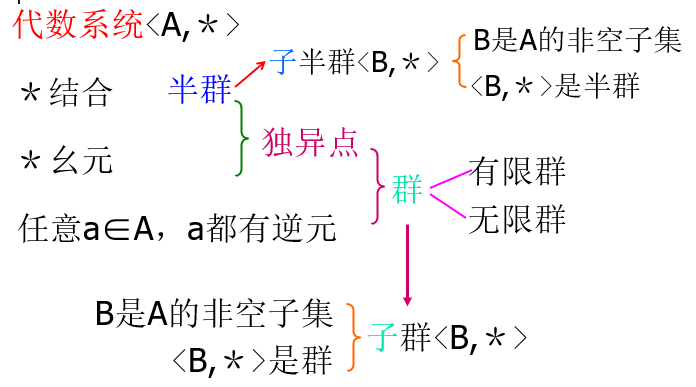
- \(<A,*>\)是[[群#独异点|独异点]]
- 证明:
- 证明该运算结合
- 证明该运算存在幺元(左幺元、右幺元)
- 证明每一个元素都存在逆元
性质
- 设\(<G,*>\)是群,对任意\(a\in G\)有\((a^{-1})^{-1}=a\)

- 设\(<G,*>\)是群,对任意\(a,b\in G\)有\((a*b)^{-1}=b^{-1}*a^{-1}*\)

- 群\(<G,*>\)中不可能有零元

- 群\(<G,*>\)中幺元\(e\)是唯一幂等元

- 消去律:设群\(<G,*>\),任意\(a,b,c\in G\)
- 左消去率:若\(a*b=a*c\),则\(b=c\)
- 右消去律:若\(b*a=c*a\),则\(b=c\)
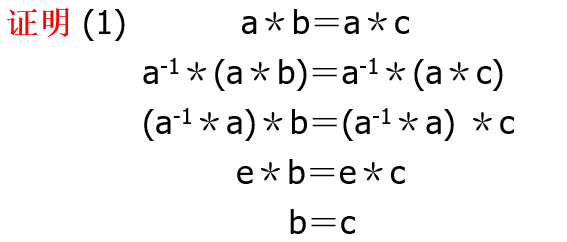
- 设群\(<G,*>\),任意\(a,b\in G\),方程\(a*x=b\)与\(y*a=b\)都有唯一解

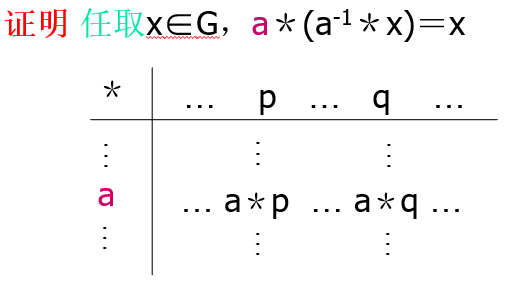
- 群\(<G,*>\)运算表中的每行或每列都是\(G\)上的一个置换
元素的阶
- 定义:设\(e\)是群\(<G,*>\)的幺元,\(a\in G\),满足\(a^k=e\)的最小正整数\(k\),称为元素\(a\)的阶,记作\(|a|\)
- 有限群中每个元素的阶均有限
子群
子群的定义

子群的性质
- 设\(<S,*>\)是\(<G,*>\)的子群,则
- 拥有共同的幺元
- 元素具有相同的逆元
子群的判定
- 设群\(<G,*>\),\(S\subseteq G\)且\(S\neq \varnothing\),则\(<S,*>\)是\(<G,*>\)的子群,当且仅当:
- 封闭:对\(\forall a, b \in S\),有\(a*b\in S\)
- 对\(\forall a \in S\),有\(a^{-1} \in S\)
子群的陪集
集合的积



陪集
