跳转至

集合与关系

集合的概念

集合及其表示

子集与空集

幂集

  • 幂集：以A的全部子集为元素组成的集合，记作\(P(A)\)或\(2^A\)
    • 幂集的元素为集合
  • 设A为有限集，\(|A|=n\)，则\(|P(A)|=2^n\)
  • 幂集的表达方式：

集合的运算

- 对称差 - 对称差的性质：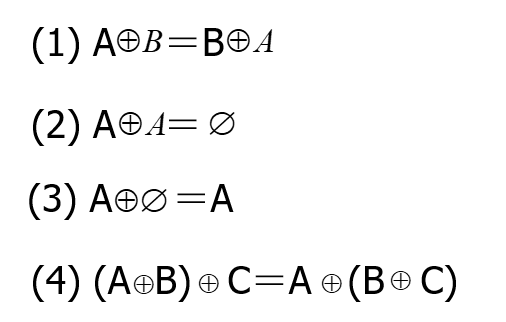

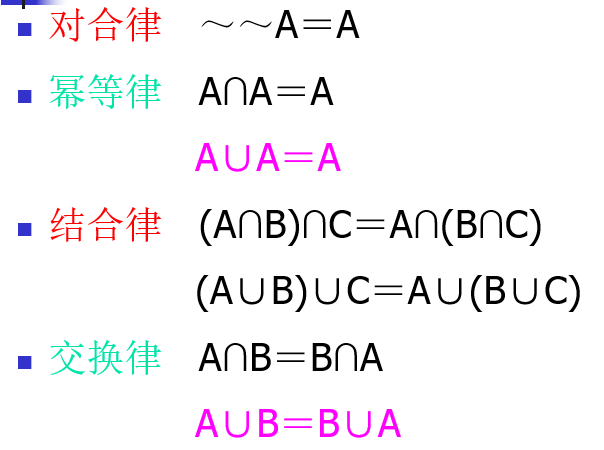
集合运算的基本性质

序偶与笛卡尔积

n元组

  • n元组：有序组\(<a_1,a_2,...,a_n>\)
  • 二元组被称为序偶

笛卡尔积的概念

  • 笛卡尔积：集合A与集合B的笛卡尔积\(A×B=\{<a,b>|a\in A, b \in B\}\)
    • 若\(A=\varnothing\)或\(B=\varnothing\)，则\(A×B=\varnothing\)
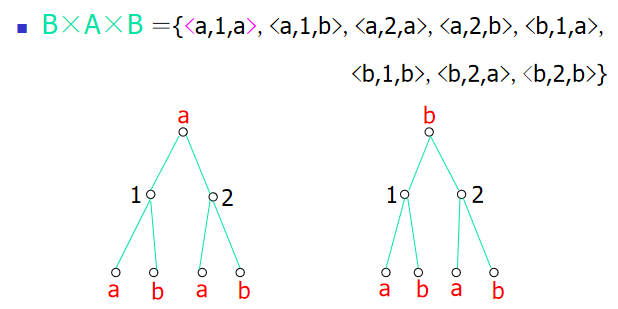
  • 不满足交换律与结合律：
    • \(A \times B \neq B \times A\)
    • \(( B \times A ) \times B \neq B \times ( A \times B )\)

笛卡尔积的性质

  • 设A、B、C、D为集合
    • 对于任意ABC集合，分配律：
      • \(A\times (B\cap C)=(A \times B)\cap(A \times C)\)
      • \((B \cap C)\times A=(B \times A)\cap(C \times A)\)
      • \(A \times(B \cup C)=(A \times B)\cup(A \times C)\)
      • \((B \cup C)\times A=(B \times A)\cup(C \times A)\)
    • C非空：\(A \subseteq B \Leftrightarrow A \times C \subseteq B \times C \Leftrightarrow C \times A \subseteq C \times B\)
    • ABCD为任意非空集合：\(A \times B \subseteq C \times D\)，当且仅当\(A \subseteq C,B \subseteq D\)

关系及其表示

关系的概念

关系的前域与值域

集合A到B的关系

  • 集合A到B的关系：笛卡尔积\(A\times B\)的子集称为A到B的关系
    • A到B的空关系
    • A到B的全域关系
    • 集合A上的关系：\(A\times A\)的关系

关系矩阵

关系图

关系的性质

恒等关系

\(\(I _ { A } = \{ < x , x > x \in A \}\)\)

自反关系和反自反关系

  • 自反关系：对\(\forall x \in A\)均有\(<x,x>\in R\)，则称\(R\)为\(A\)上的自反关系 ^059c7e
    • 自反关系包含了恒等关系
  • 反自反关系：对\(\forall x \in A\)均有\(<x,x>\notin R\)，则称\(R\)为\(A\)上的自反关系

    [!Question] - How many relations are there on a set with n elements？ - \(2^{{n}^2}\) - How many reflexive relations are there on a set with n elements? - \(2n\)

对称关系和反对称关系

  • 对称关系：\(\forall x, y\in A\)，每当\(<x,y>\in R\)时必有\(<y,x>\in R\)，则称R为A上的对称关系 ^8b0a70
  • 反对称关系：\(\forall x, y\in A\)，每当\(<x,y>\in R\)且\(<y,x>\in R\)有\(x=y\)，则称R为A上的对称关系

传递关系

^3ee3e3 - 传递关系：设任意集合\(A\)，\(R \subseteq A \times A\)，对\(\forall x, y, z \in A\) - 若\(<x, y>\in R\) 且\(<y, z>\in R\)时，必有\(<x, z>\in R\)

等价关系与划分

等价关系的概念

  • 等价关系：[[集合与关系#059c7e|自反关系]]、[[集合与关系#8b0a70|对称关系]]、[[集合与关系#传递关系|传递关系]]

等价类与商集

  • 等价类：设\(R\)为集合\(A\)上的等价关系，\(a\in A\)，\(a\)确定的关于\(R\)的等价类：
    • \([a]_R = \{x | x\in A, <x,a>\in R\}\quad <a,x>\in R\)
  • 商集：集合\(A\)关于\(R\)的商集，即等价类的集合
    • \(A/R = \{[a]_R | a\in A\}\)
  • 定理：设\(R\)为\(A\)上的等价关系，对于\(a, b \in A\)
    • 有\([a]_R = [b]_R \Leftrightarrow aRb\)
    • 有\([a]_R \cap [b]_R = \emptyset \Leftrightarrow a\bar{R} b\)

划分的概念

  • 划分类似于一个分类问题，每一个类别不重叠

划分一一对应等价关系

  • 每一个划分都可以对应一个等价关系，这个划分即为这个等价关系的商集

偏序关系

概念

  • 偏序关系：设A为任意集合，R为A上的关系，若R是自反、反对称和传递关系，则称R为A上的偏序关系，记作\(\preccurlyeq\)
    • 偏序集：序偶\(<A,\preceq>\)
    • \(<a,b>\in\preccurlyeq \quad\Leftrightarrow \quad a\preccurlyeq b\)
    • 可比与不可比：，设偏序集\(<A,\preccurlyeq>\)，若\(a,b\in A\)，则称其可比，否则不可比
  • 拟序关系：设A为任意集合，R为A上的关系，若R是反自反、反对称和传递关系，则称R为A上的拟序关系，记作\(\prec\)
    • 拟序集：\(<A,\prec>\)
    • \(x\prec y\)当且仅当\(x\preccurlyeq y\)但\(x\neq y\)
  • 拟序关系与偏序关系：
    • \(\preccurlyeq - I_A\)是A上的拟序关系
    • \(\prec\cup I_A\)是A上的偏序关系

盖住关系

  • 盖住关系：设偏序集\(<A,\preccurlyeq>\)，若A中不存在其他元素z，使\(a\prec z, z\prec b\)，则称元素b盖住a
    • \(cov(A)=\{<a,b>|a,b\in A,b 盖住 a\}\)

#离散大题 哈斯图

  • 作图规则：
    • 用结点代表A中的元素
    • 如果\(a\prec b\)，则将结点b画在结点a之上
    • 若\(<a,b>\in cov(A)\)，则将a、b连接

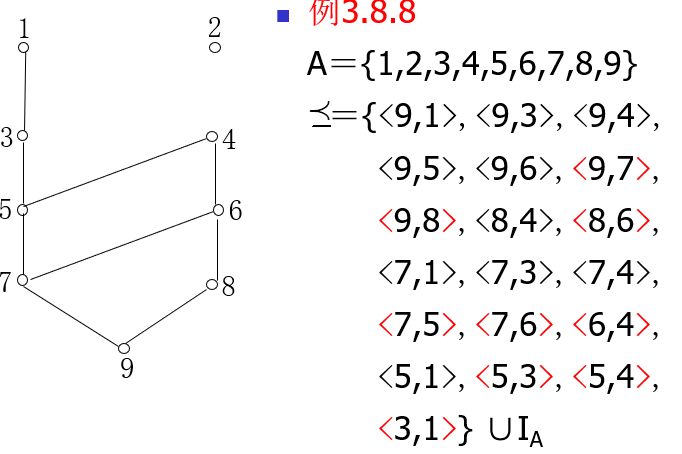
最大元、极大元、上界

  • 最blabla元
    • 对于每个\(x\in A\)均有\(x\preccurlyeq a\)，则称\(a\)为\(<A,\preccurlyeq>\)的最大元
    • 对于每个\(x\in A\)均有\(a\preccurlyeq x\)，则称\(a\)为\(<A,\preccurlyeq>\)的最小元
  • 极blabla元
    • 若不存在其他元素\(x\in A\)使\(a\preccurlyeq x\)，则称\(a\)为\(<A,\preccurlyeq>\)的极大元
    • 若不存在其他元素\(x\in A\)使\(x\preccurlyeq a\)，则称\(a\)为\(<A,\preccurlyeq>\)的极小元
  • 最blabla元一定是极blabla元