跳转至

逻辑回归(Logistic Regression)

模型

Sigmoid(0~1)

代价函数：交叉熵(Cross Entropy)

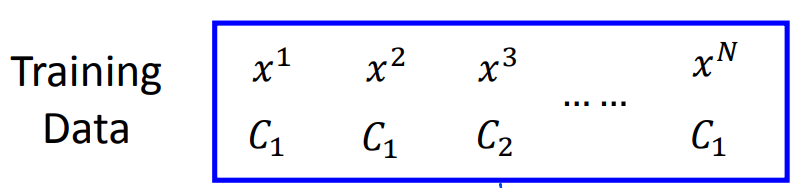
image.png

推导过程

\[L(w,b) = f_{w,b}(x^1)f_{w,b}(x^2)(1-f_{w,b}(x^3))……f_{w,b}(x^n)$$ $$w^*,b^* = arg \max_{w,b}L(w,b)=arg\min_{w,b}-\ln{L(w,b)}$$ $$-\ln{L(w,b)}=\sum_n -[\hat{y}\ln{f_{w,b}(x^n)+(1-\hat {y}^n)\ln{1-f_{w,b}(x^n)}}]\]

意义

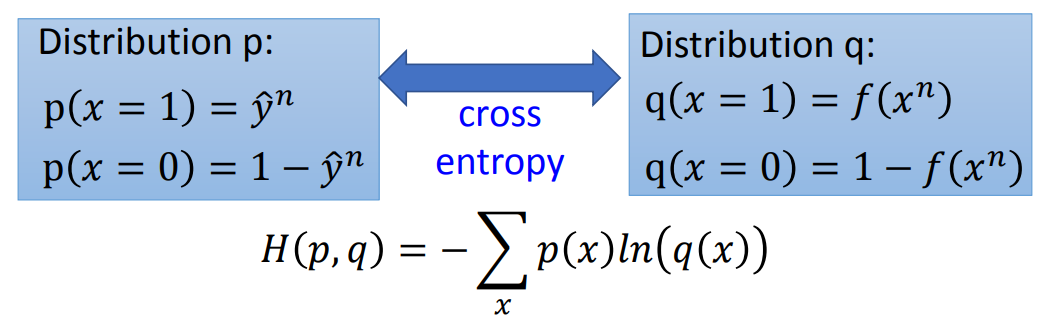
交叉熵越小代表两个Distribution越接近，完全相同时为0，用于逐渐逼近真实概率、评判参数的好坏 image.png

目的

通过优化，不断减小交叉熵(Cross Entropy)

为什么不使用Square Error

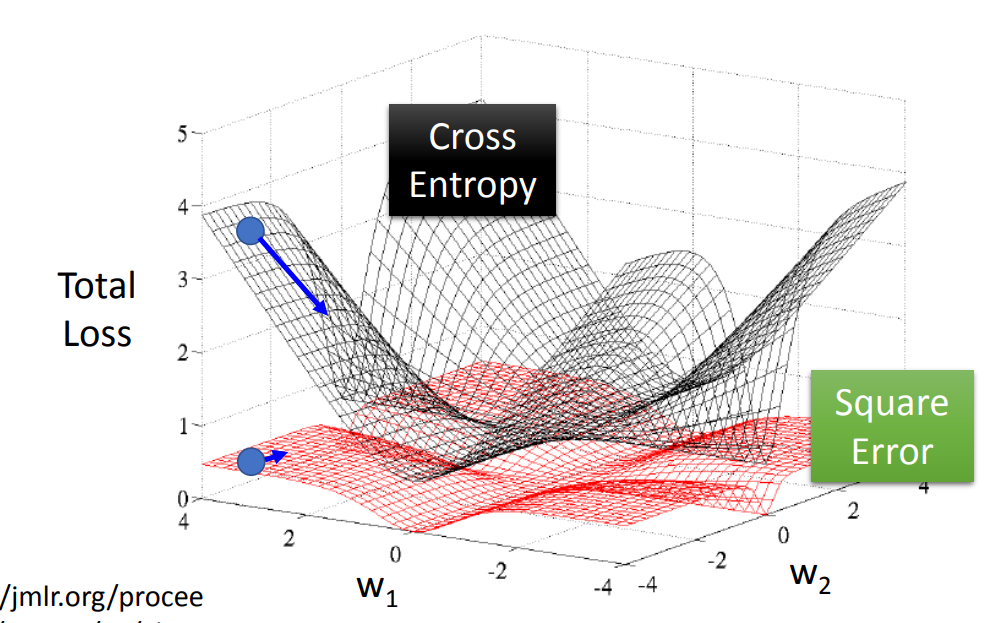image.png - 对于Square Error：在远离最优点和最优点处的变化率都相对较小 - 固定学习率：在远离最优点时，学习慢 - 自适应学习率：无法判断当前与最优点的距离，而采用了错误的学习率

优化(Optimizer)

  • BP
  • 使用梯度下降 \(\(w_i \leftarrow w_i - \eta\sum_n-(\hat y^n -f_{w,b}(x^n))x_i^n\)\)

区别

判别模型与生成模型(Discriminative and Generative)

\(\(P(C_1|x)=\sigma(w·x+b)\)\) 同样的模型，选择不同的函数可能有不同的结果

判别模型(Discriminative)

  • 直接找到\(w\)和\(b\)
  • 一般来说，更好（先验概率对生成模型的影响）

生成模型(Generative)

  • 通过高斯分布，找\(\mu^1、\mu^2、\Sigma^{-1}\)，\(\(\begin{array}{ll} w^T=(\mu^1-\mu^2)^T\Sigma^{-1} \\ b=-\frac{1}{2}(\mu^1)^T(\Sigma^1)^{-1}\mu^1+\frac{1}{2}(\mu^2)^T(\Sigma^2)^{-1}\mu^2+\ln{\frac{N_1}{N_2}}\\ \end{array}\)\)

多个类别分类(Multi-class Clasification)

\[\begin{array}{ll} \mathrm{C}_{1}: w^{1}, b_{1} & z_{1}=w^{1} \cdot x+b_{1} \\ \mathrm{C}_{2}: w^{2}, b_{2} & z_{2}=w^{2} \cdot x+b_{2} \\ \mathrm{C}_{3}: w^{3}, b_{3} & z_{3}=w^{3} \cdot x+b_{3} \end{array}\]

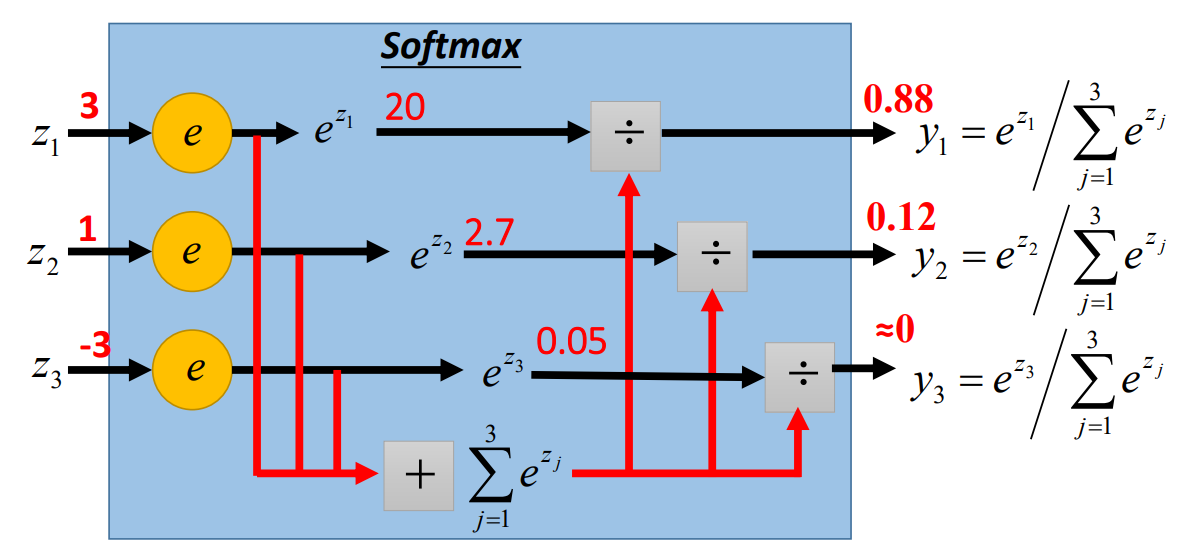
Softmax

  • 功能：
    • 归一化
    • 放大差异

Logistic Regression的限制

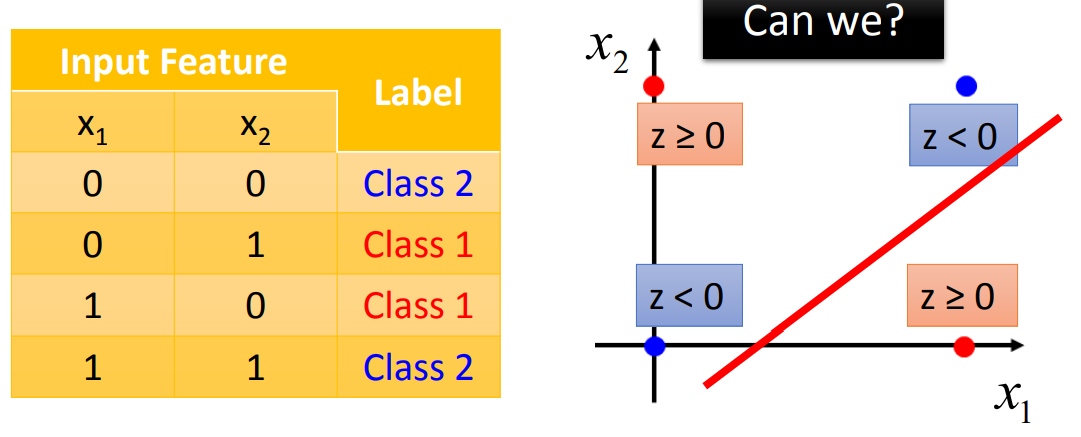- 方案：选择其他特征