跳转至

回归问题

机器学习

  • 让机器具备找一个函数的能力

回归问题

定义模型

  • 带有未知参数的函数：(\(eg:y=b+w*x_1\)\)
    • \(y\)是要预测的东西
    • \(x_1\)是已知信息
    • \(b\)与\(w\)是未知的参数，机器学习即找参数
  • 难点在于模型的设计
  • 使用大量的函数叠加，组合成任意函数：\(\(y = b + \sum _i c_isigmoid(b_i+\sum _j w_{ij}x_{j})\)\)

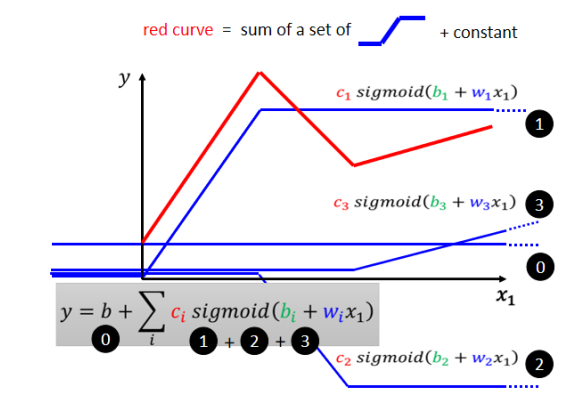
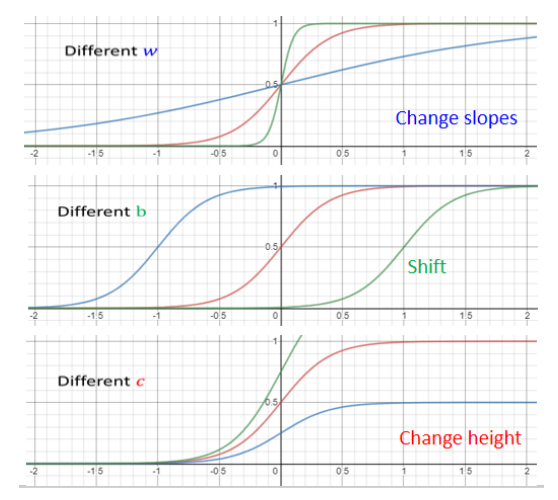
Sigmoid

\(\(y=c\frac {1}{1 + e^{-(b + wx_1)}}\)\)

ReLU

\(\(y=c*max(0,b+wx_1)\)\)

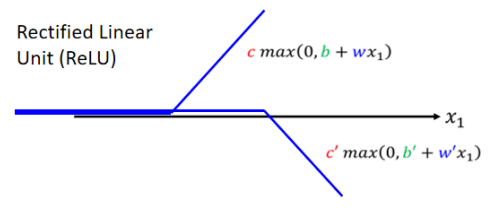
  • Sigmoid和ReLU这样的函数在机器学习中称为激活函数(Activation Function)

定义代价函数

  • 用于评判模型中参数的好坏
  • MSE(mean square error)：\(\({ L(f) =\sum ^{i}_{n = 1}(\hat{y}^n - f(x^n))^2 }\)\)
  • MAE(mean absolute error)：\(\({ L(f) =\sum ^{i}_{n = 1}\lvert \hat{y}^n - f(x^n)\rvert }\)\)

选择优化器