基本术语
图的类型
- 图通常使用一个二元组\(G=<V, E>\)表示，V为顶点集，E为边集
- 无向图：无方向，边使用圆括号表示
- 有向图：有方向，弧使用尖括号表示\(<v_1,v_3>\) ，\(v_1\)为弧尾，\(v_3\)为弧头
- 简单图：及不含平行边也不含环的图称为简单图
- 完全图：
- 无向图中，任意两个点都有一条边
- 每个顶点到其他\(n-1\)个顶点都有边，一共有\(\frac{n(n-1)}{2}\)条边
- 有向图中，任意两个点都有两条方向相反的弧
- 每个顶点发出\(n-1\)条边，且进来\(n-1\)条边
- 共\(n(n-1)\)
- 稀疏图与稠密图：一般来说：\(\left\vert E \right\vert < \left\vert V \right\vert*\log{\left\vert V \right\vert}\) ,为稀疏图
- 邻接和关联：
- 邻接：指顶点和顶点之间的关系
- 关联：指边和顶点之间的关系
- 顶点的度：与该顶点相关联的边的数目
- 路径、路径长度和距离
- 路径：接续的边的顶点构成的序列
- 路径长度：路径上边或弧的数目
- 距离：从顶点到另一顶点的最短路径长度
- 回路（环）、简单路径和简单回路
- 回路：第一个顶点和最后一个顶点相同的路径
- 简单路径：除路径起点和终点可以相同外，其余顶点均不相同的路径
- 简单回路：除路径起点和终点相同外，其余顶点均不相同的路径
- 欧拉回路：经过图中各边恰好一次的回路
- 子图与生成子图
- 子图：设有两个图：\(G=(V,E)、G_1 = (V_1, E_1)\)，其中，\(V_1\subseteq V、E_1\subseteq E\) ,则称\(G_1\)为\(G\)的子图
- 生成子图：从图中选择所有的顶点，若干条边构成的图称为原图的生成子图
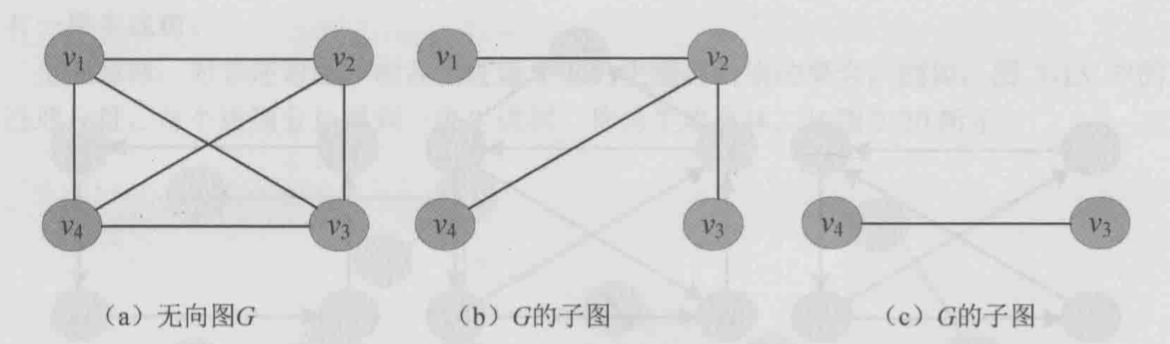^e89c2f
这次一定弄懂完全图、连通图、连通分量、强连通图、强连通分量、极大连通分量、极小联通分量、生成树、生成森林的区别_小小的香辛料的博客-CSDN博客_完全图和连通图区别
- 连通图和连通分量
- 连通图：任何两个顶点都是连通的（如上图中的(a)）
- 连通分量：无向图\(G\)的极大连通子图称为\(G\)的连通分量
- 极大连通子图：该子图是\(G\)的连通子图，如果再加入一个顶点，该子图不连通
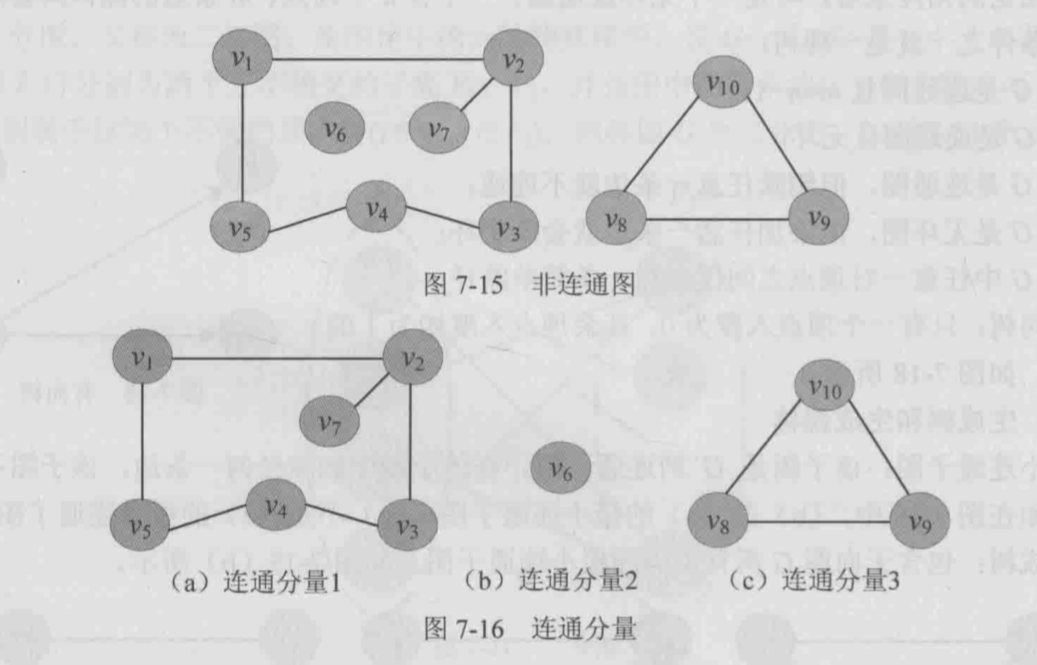
- 强连通图和强连通分量
- 强连通图：在有向图中，任何两个顶点之间都有路径
- 强连通分量：有向图\(G\)的极大强连通子图称为\(G\)的强连通分量
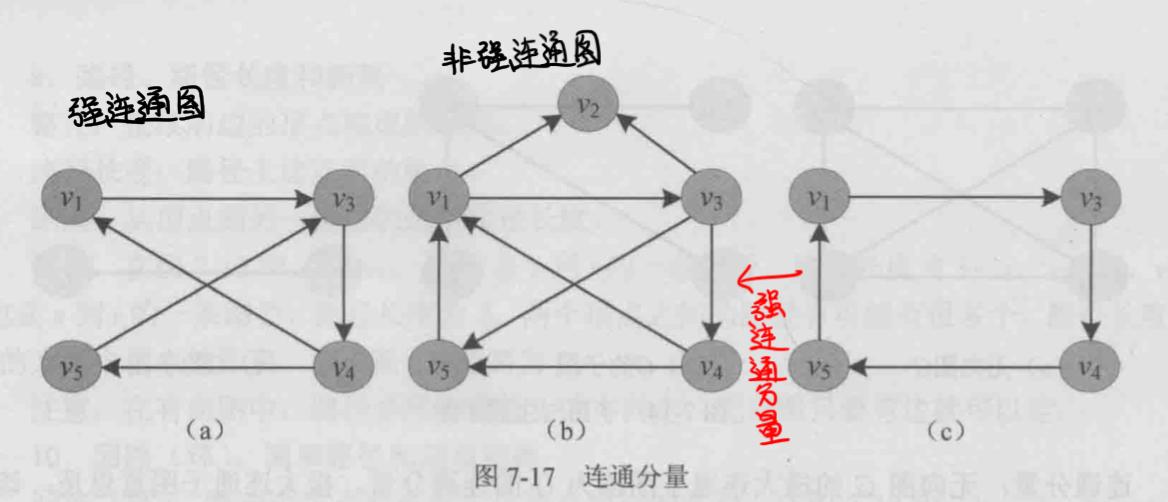
- 树和有向树
- 从图论的角度来看，树是一个无环连通图，需要满足以下五个条件：
- \(G\)是连通图且\(m=n-1\)
- \(G\)是连通图且无环
- \(G\)是连通图，但删除任意一条边就不连通
- \(G\)是无环图，但添加任意一条边就会产生环
- \(G\)中任意一对顶点之间仅存在一条简单路径
- 生成树和生成森林
- 极小连通子图：删除任何一条边，该子图都不在连通
- 生成树：包含无向图G所有顶点的极小连通子图 ^c58be0
- 生成森林：对非连通图，由各个连通分量的生成树组成的集合
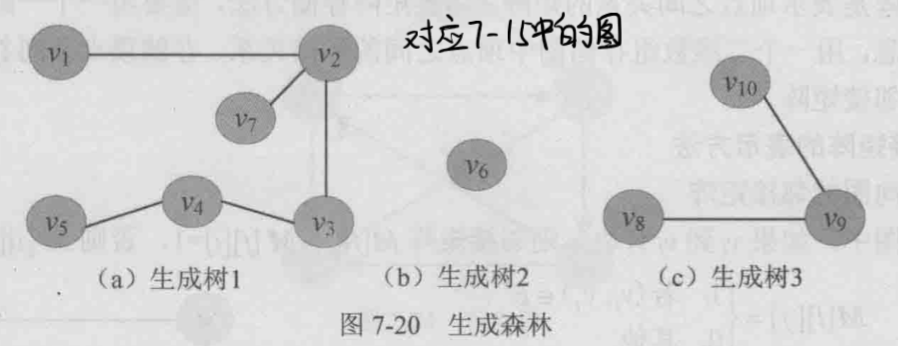
- 二分图：如果顶点集V可分割为两个互不相交的子集，且每条边所关联的两个顶点分别属于两个不同的顶点集
边的分类
- 树边：深度优先森林中的边
- 后向边：后向边\((u,v)\)是将结点\(u\)连接到其在深度优先树的祖先节点\(v\)
- 自循环也被认为是后向边
- 前向边：前向边\((u,v)\)是将结点\(u\)连接到其在深度优先树的后代节点\(v\)
- 横向边：其他所有边