跳转至

二叉树

定义

  • 每个节点至多只有两颗子树
  • 子树存在左右之分，次序不能任意颠倒

性质

  1. 在二叉树的第\(i\)层上至多有\(2^{i-1}\)个节点
  2. 深度为\(k\)的二叉树至多有\(2^k-1\)个节点(\(k>=1\))
  3. 对任何一棵二叉树T，如果其终端结点树为\(n_0\)，度为2的结点数为\(n_2\)，则\(n_0=n_2+1\)
  4. 满二叉树：深度为\(k\)且有\(2^k-1\)个结点的二叉树，即每层都有最大节点数
  5. 完全二叉树：除最后一层外，每一层都是满的
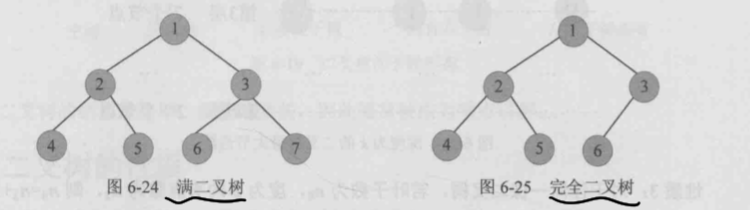
  6. 对于完全二叉树，若从上至下，从左至右编号，则编号为i的结点，左孩子的编号一定为\(2i\)，右孩子的编号一定为\(2i+1\)，双亲的编号一定为\(i/2\)，这样的特点方便了后续使用一维数组存储二叉树
  7. 一个具有\(n\)个节点的完全二叉树,其叶子节点的个数\(n_0\)为:\(\lceil \frac{n}{2} \rceil\) ，或者\(\lfloor \frac{n+1}{2} \rfloor\)

二叉树的存储结构

顺序存储结构

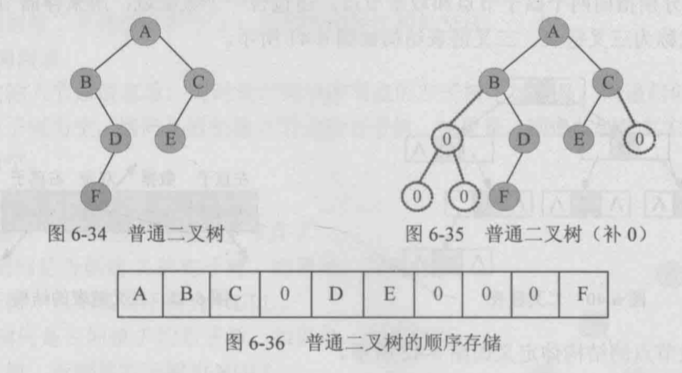
完全二叉树的顺序存储 - 非常适用于完全二叉树的存储 - 对于普通二叉树的存储，可以在其他位置上补0，或其他标志，代表当前位置没有孩子 （浪费空间） 普通二叉树的存储

链式存储结构

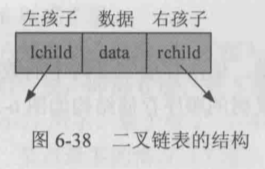
  • 使用二叉链表存储 
    struct BiNode{
    char data;                    //数据域
    BiNode *lchild,*rchild;       //左右孩子
};

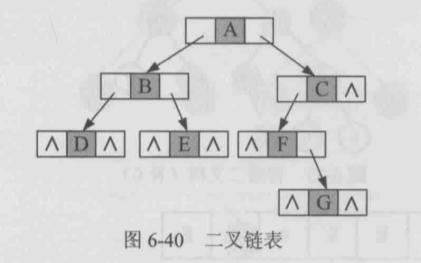
  • 使用三叉链表存储

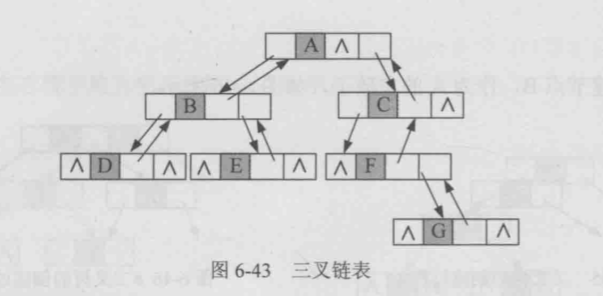
二叉树的创建

二叉树的各种创建方法_玲max的博客-CSDN博客_二叉树的创建 1. 补空法 1. 利用先序遍历的顺序，进行创建 2. 数据通过命令行输入 3. 空结点使用特殊字符表示

注意：由于使用的时先序遍历的方式，从第一个字符到第一个特殊字符（代表空）的前一个字符的数量为二叉树的层数，在测试的时候要适量，否则数量过多的话，二叉树的层数过多，可能让结点数量过多，产生程序错误的错觉 2. 代码实现： 

void CreateBiTree(BiNode* &p){
    char x;
    cin >> x;
    if(x == '#') p = NULL;              //输入特殊字符时为空
    else{
        p = new BiNode;
        p->data = x;
        CreateBiTree(p->lchild);        //进行左孩子的创建
        CreateBiTree(p->rchild);        //进行右孩子的创建
    }
}

二叉树的遍历

  • 使用递归实现对二叉树的遍历
  • 实际上时将一个非线性结构进行线性化的操作

先序遍历

  • 步骤
    1. 访问根节点
    2. 先序遍历左子树
    3. 先序遍历右子树

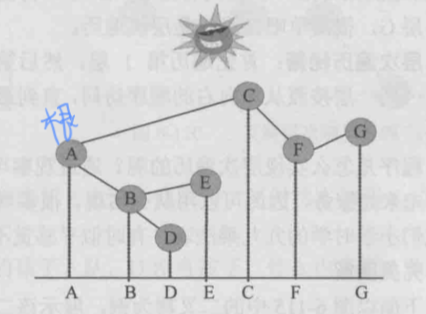- 代码实现： 

void PreOrderTravellser(BiNode* &p){
    if(p == NULL) return;
    cout << p -> data << endl;
    PreOrderTravellser(p->lchild);
    PreOrderTravellser(p->rchild);
}

中序遍历

  • 步骤
    1. 中序遍历左子树
    2. 访问根节点
    3. 中序遍历右子树

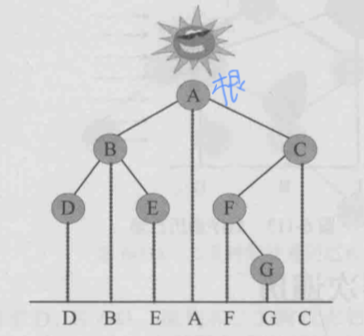- 代码实现： 

void InOrderTravellser(BiNode* &p){
    if(p == NULL) return;
    InOrderTravellser(p->lchild);
    cout << p->data << endl;
    InOrderTravellser(p->rchild);
}

后序遍历

  • 步骤
    1. 后序遍历左子树
    2. 后序遍历右子树
    3. 访问根节点

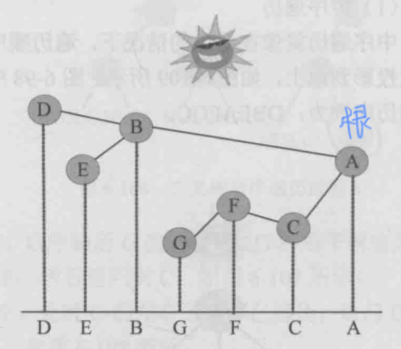- 代码实现： 

void PostOrderTravellser(BiNode* &p){
    if(p == NULL) return;
    PostOrderTravellser(p->lchild);
    PostOrderTravellser(p->rchild);
    cout << p->data << endl;
}

先序、中序、后序遍历之间的区别仅仅是先输出、递归左孩子、递归右孩子的顺序之间的区别

层次遍历

  • 逐层往下遍历

线索二叉树

引入：

二叉树采用二叉链表存储时，每个节点有两个指针域，如果二叉链表有\(n\)个节点，则一共有\(2n\)个指针域，而只有\(n-1\)个是实指针，其余\(n+1\)个都是空指针，为了充分利用空指针，我们使用空指针记录节点的前驱或后继的信息 - 前驱与后继：指以特定的方式遍历时，线性化之后的前驱和后继

方法：

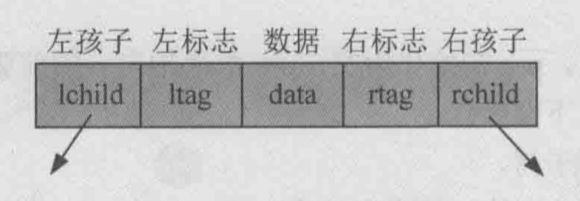
如果节点有左孩子，则lchild指向左孩子，否则lchild指向其前驱，右孩子同理，同时，再使用一个标志域，区分指向的是孩子还是前驱/后继，节点如下图： 线索链表节点

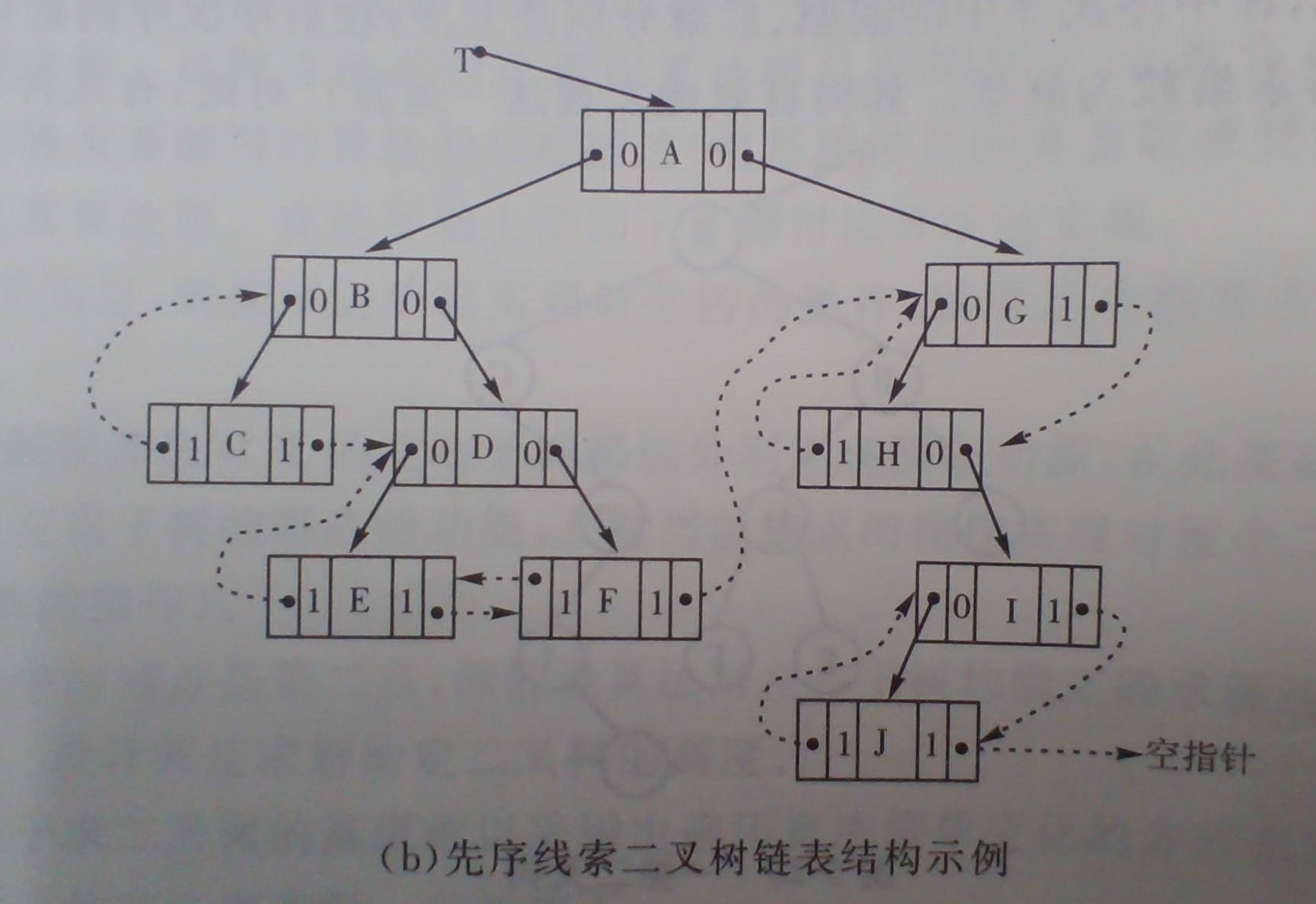
先序线索二叉树链表结构

概念

  • 线索链表：带有标志域的二叉链表
  • 线索：指向前驱和后继的指针
  • 线索二叉树：带有线索的二叉树
  • 线索化：以某种遍历方式将二叉树转化为线索二叉树的过程

构造线索二叉树

  • 二叉树线索化的过程，实际上实在遍历过程中修改空指针的过程
    • 如果当前节点p的左孩子为空，则该节点的lchild指向其前驱，即p->lchild=pre
    • 如果pre节点的右孩子为空，则该节点的rchild指向其后继，即pre->rchild=p

遍历线索二叉树

  • 利用前驱和后继的信息进行遍历

    对于频繁的查找前驱和后继的运算，线索二叉树优于普通二叉树 对于插入和删除操作，线索二叉树比普通二叉树开销大（除了插入和删除外，还需要修改相应的线索）

应用

  1. [[树表查找#二叉查找树|二叉查找树]]