#计组重点 定点运算
移位运算
在计算机中,移位运算和加减配合,可以实现乘除运算 - 规则:
- 对负数移位运算的解释: - 核心:移位前后的符号不变,符合对应表达方式的符号表示 - 原码:移位时候保证最高位的符号位不变即可,所以左移或右移补0不影响 - 补码 : - 左移:补0 - 右移:补1 - 反码:1 左移与右移对于原数字的影响 - 左移:高位移丢,导致原有的数据错误 - 右移:低位移丢,可能导致精度降低,但不至于使数据偏差过大 在后续的浮点数计算中,在进行对阶时,也依据此原理,将小的阶码向大的阶码对齐
算数逻辑运算与逻辑移位的区别 - 有符号数的移位称为算数移位 - 无符号数的移位称为逻辑移位
加法与减法运算
补码加减运算
- 加法:
- 整数:\([A]_补+[B]_补=[A+B]_补(\mod2^{n+1})\)
- 小数:\([A]_补+[B]_补=[A+B]_补(\mod 2)\)
- 减法:
- 整数:\([A-B]_补=[A]_补+[-B]_补(\mod2^{n+1})\)
- 小数:\([A-B]_补=[A]_补+[-B]_补(\mod2)\)
取模是为了应对溢出的情况
- 例题:

对于溢出的判断
- 一位符号判断溢出:
- 参加操作的两个数符号相同,其结果与源操作数的符号不同,则溢出
- 次高位的进位与高位的进位进行异或,若为
1则溢出
- 两位符号判断溢出:结果的两个符号位不同
乘法运算
- 考虑笔算乘法:
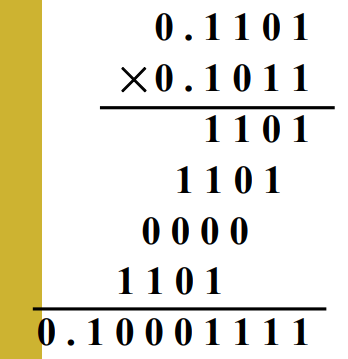
- 符号位单独处理
- 乘数的某一位决定是否加被乘数
- 乘积的位数扩大一倍
- 将竖式横置:

- 启发:我们可以使用移位运算和加法运算结合来实现乘法运算
- 由此,我们可以使用类似递归的方法来实现乘法运算
- 进一步将其转换为表格的形式:
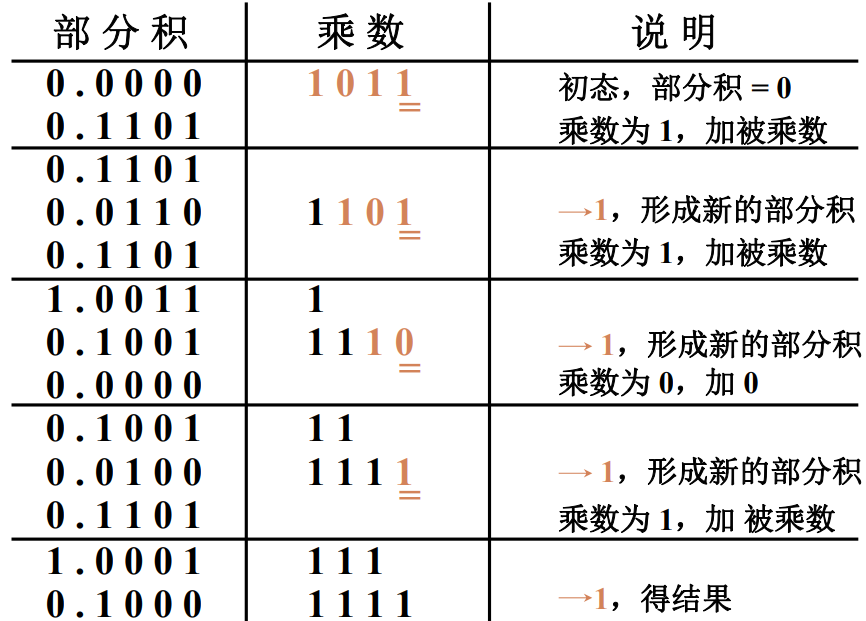
- 每一步包含了:
- \(A>>1\)
- \(I = 乘数的最低位*被乘数\)
- \(A=A+I\)
- 每一步包含了:
原码乘法
- 符号位单独处理:\(x_0\oplus y_0\)
- 数值部分:\(x*y\)
对于反码和补码的乘法处理是一致的,一个是取绝对值的操作,另一个是符号的计算
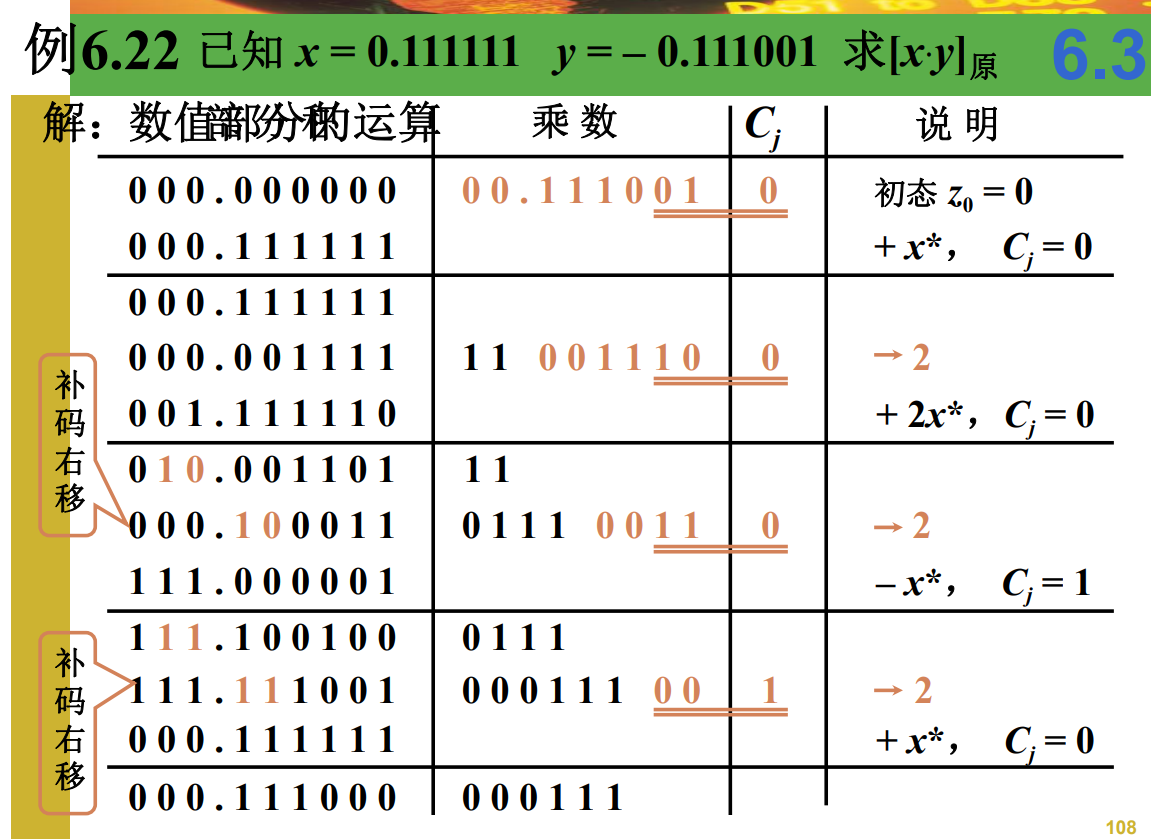
原码两位乘
- 两位乘:每次用乘数的2位判断原部分积是否加和如何加被乘数
[!attention] 在原码两位乘中,操作数是绝对值的补码,所以在进行移位的时候需要注意负数的情况
- 一个初步的两位乘表格:
- 问题:不方便计算
| 乘数\(y_{n-1}y_n\) | 新的部分积 |
|---|---|
| 00 | +0倍, >>2 |
| 01 | +1倍, >>2 |
| 10 | +2倍, >>2 |
| 11 | -1倍(借一位)+4倍, >>2 |
| - 改良后的表格: |
| 乘数\(y_{n-1}y_n\) | 标志位\(C_j\) | 操作内容 |
|---|---|---|
| 00 | 0 | \(z>>2, y>>2, C_j=0\) |
| 01 | 0 | \(z+x>>2, y>>2, C_j=0\) |
| 10 | 0 | \(z+2x>>2, y>>2, C_j=0\) |
| 11 | 0 | \(z-x>>2, y>>2, C_j=1\) |
| 00 | 1 | \(z+x>>2, y>>2, C_j=0\) |
| 01 | 1 | \(z+2x>>2, y>>2, C_j=0\) |
| 10 | 1 | \(z-x>>2\), \(y>>2,\) \(C_j=1\) |
| 11 | 1 | \(z>>2\), \(y>>2\), \(C_j=1\) |
 |
- 原码两位乘和原码一位乘比较:
| 你好 | 原码一位乘 | 原码两位乘 |
|---|---|---|
| 符号位 | \(x_0\oplus y_0\) | \(x_0\oplus y_0\) |
| 操作数 | 绝对值 | 绝对值的补码 |
| 移位 | 逻辑右移 | 算术右移 |
| 移位次数 | \(n\) | \(\frac{n}{2}\)(n为偶数) |
| 最多加法次数 | \(n\) | \(\frac{n}{2}+1\)(n为偶数) |
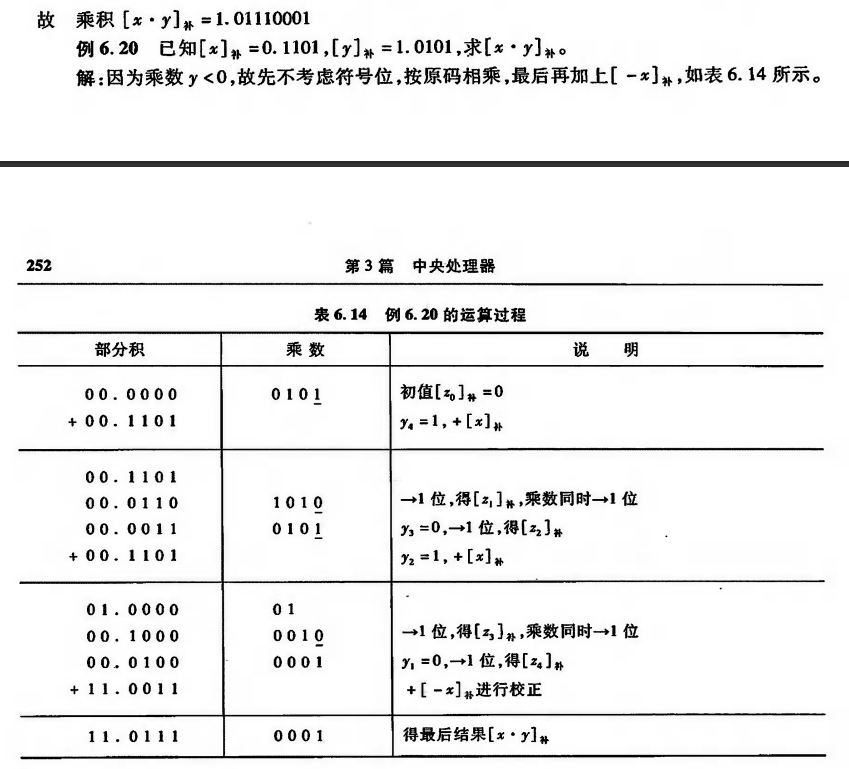
补码乘法
- 校正法:
- 乘数y为正:不管被乘数x符号如何,都可以按照原码乘法的规则进行运算
- 乘数y为负:把乘数的补码\([y]_补\)去掉符号位,当成一个整数与\([x]_补\)相乘,然后加上\([-x]_补\)进行校正
- 总结:\([x\times y]_补=[x]_补*([y]_补的{数值位})\)并且在最后根据y的正负确定是否进行校正操作
[!question] 在补码一位乘里,部分积为什么采用双符号位 补码一位乘是由重复加和移位操作实现的,移位时按补码右移规则进行。 以小数乘法为例,由于乘法过程中相加的结果可能大于1,即小数点前面第一位为数值,占去了符号位的位置,若只用移位符号位,则原符号位被破坏,在移位时候会出现错误。 如部分积采用双符号位,并以最高位代表真正的符号,就可以避免移位时候出错的现象。
[!attention] 在进行相加和移位时,需要按照补码的规则进行 - Booth算法
| \(y_iy_{i+1}\) | \(y_{i+1}-y_i\) | 操作 |
|---|---|---|
| 00 | 0 | >>1 |
| 01 | 1 | \(+[x]_补\),>>1 |
| 10 | -1 | \(+[-x]_补\),>>1 |
| 11 | 0 | >>1 |
| > [!attention] | ||
| > 在最后一步时候,不进行移位,并且符号位需要参与移位,移位的方式为算数移位 |
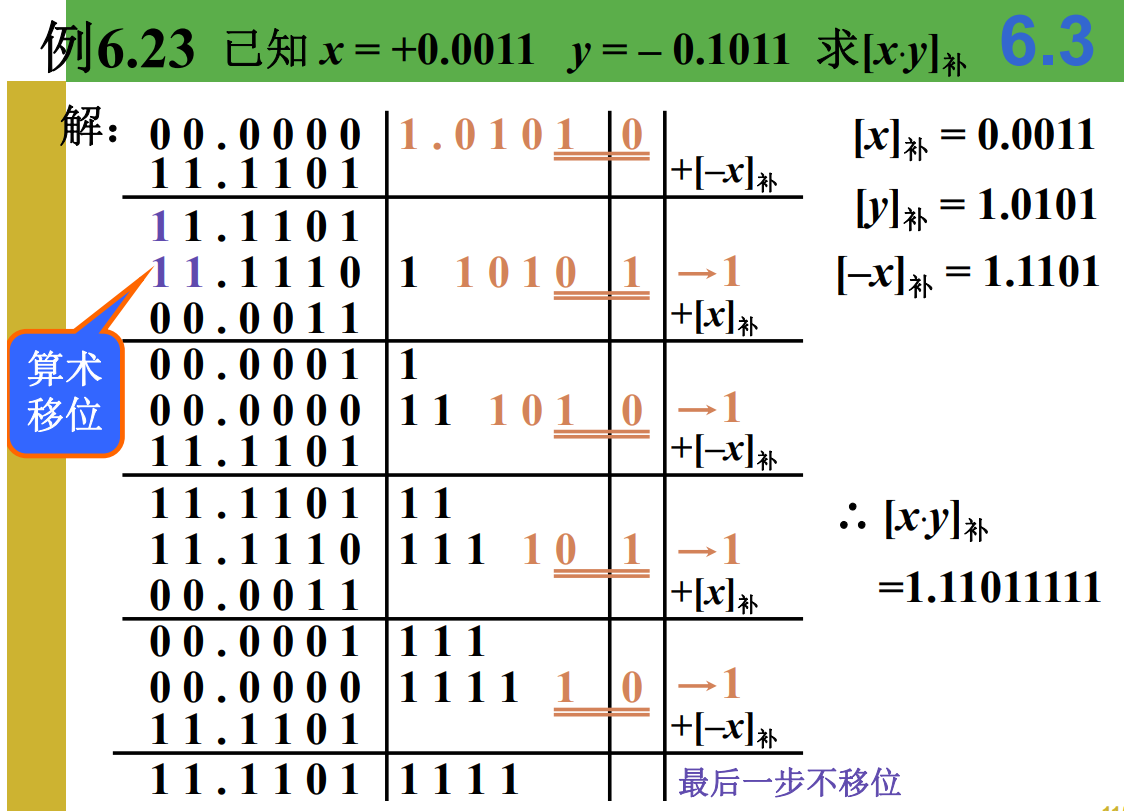
除法运算
- 笔算除法

- 笔算除法与机器除法比较:
| 笔算除法 | 机器除法 |
|---|---|
| 符号单独处理 | 符号位由异或得到 |
| 心算上商 | 通过比较大小上商 |
| 余数不动,低位补0 \(-\)右移一位的除数 |
余数左一一位,低位补0 减除数 |
| 2倍字长加法器 | 1倍字长加法器 |
| 上商位置不固定 | 在寄存器的最末尾上商 |
| ### 原码除法 | |
| - 约定: | |
| - 小数定点除法\(x^*<y^*\) | |
| - 整数定点除法\(x^*>y^*\) | |
| - 被除数不等于0 | |
| - 除数不等于0 | |
| - 预处理:当被除数和除数都\(\neq 0\),且商\(\neq 0\),才进行进一步的除法运算 | |
| > [!note] \(x^*;y^*\) | |
| > \(0.x_1x_2\cdots x_n\)为x的绝对值,记作\(x^*\) | |
| > \(0.y_1y_2\cdots y_n\)为y的绝对值,记作\(y^*\) | |
| #### 恢复余数法 | |
| - 特点:当余数为负时,加上除数,使其恢复成原来的余数 | |
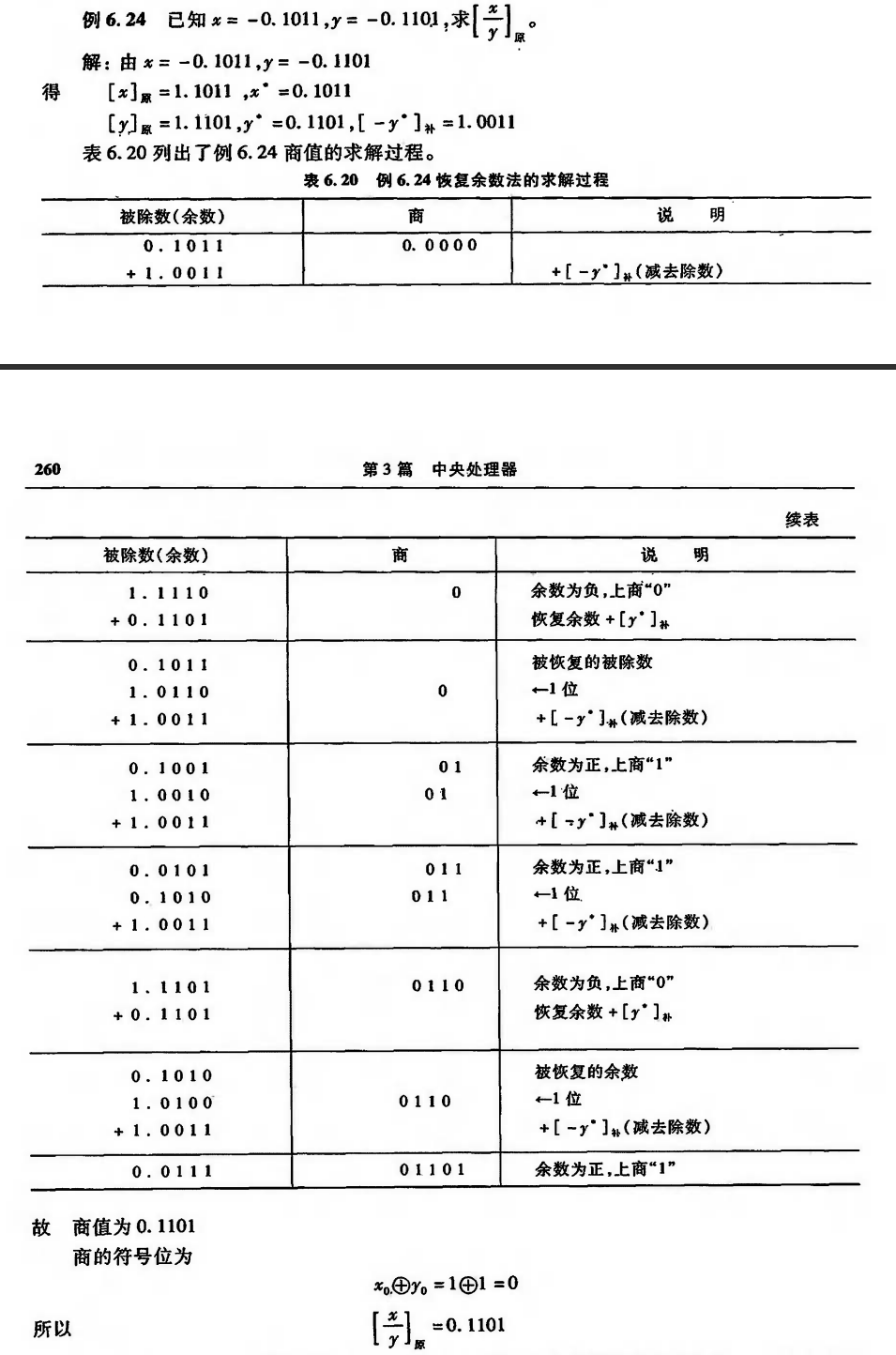 |
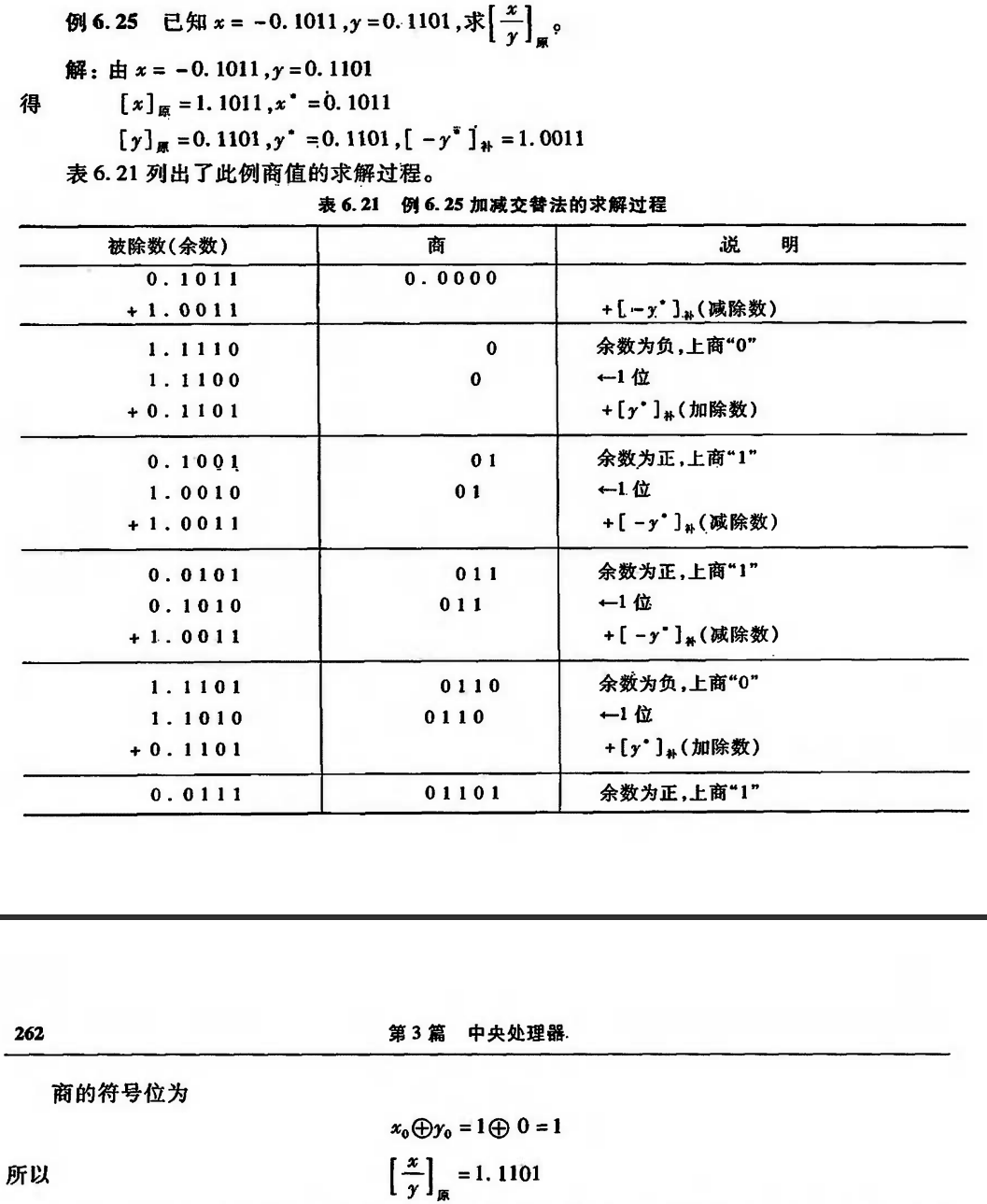
加减交替法
- 这是恢复余数法的一种改进
- 原码恢复余数法的归纳:
- 当\(R_i > 0\):上商1,做\(2R_i-y^*\)
- 当\(R_i < 0\):上商0,做\(2R_i+y^*\)
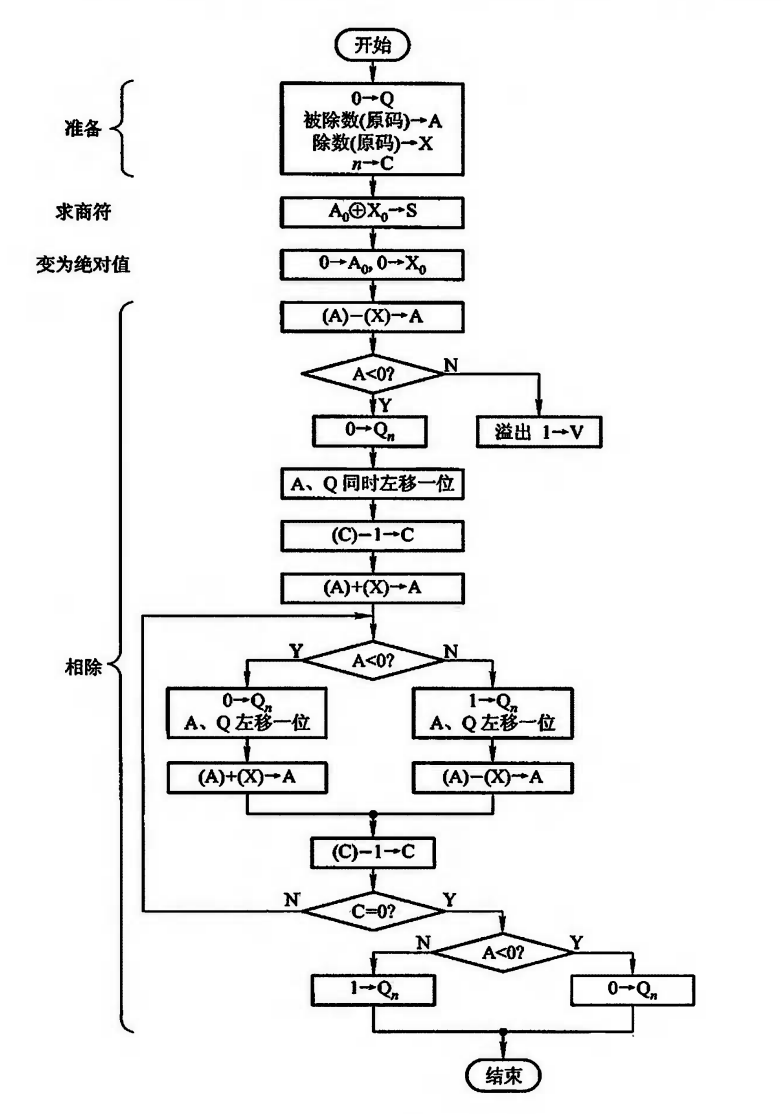
- 流程图:
补码除法
与补码乘法类似,也可以用补码完成除法操作。补码除法也分恢复余数法和加减交替法,但是加减交替法使用的比较多
[!question] 相比原码除法不够直观,主要需要解决三个问题: 1. 如何确定商值 2. 如何形成商符 3. 如何获得新的余数
商值的确定
- 比较被除数(余数)和除数的大小
- 被除数与除数同号:做减法
- 被除数与除数异号:做加法

- 商值的确定

商符的确定
- 在求商的过程中,自动根据除数与被除数的符号确定
新余数的获取
与加减交替法一致
