跳转至

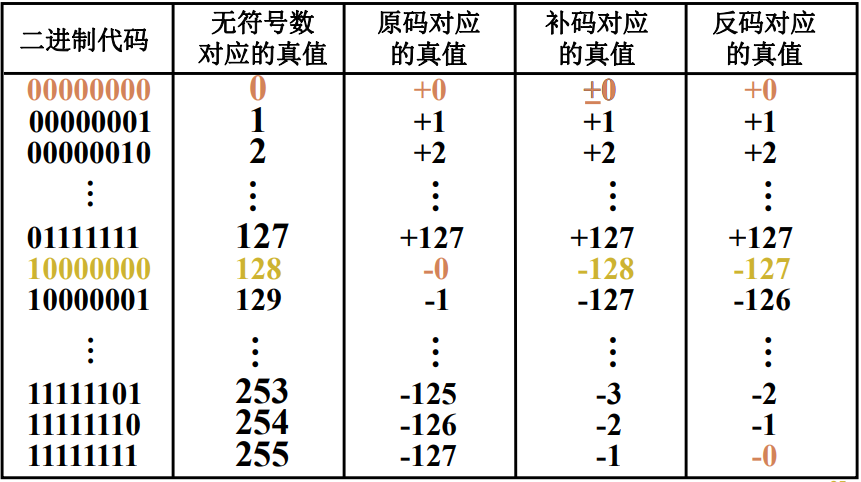
无符号数与有符号数

无符号数

  • 寄存器的位数反映无符号数的表示范围

有符号数

机器数与真值

  • 机器数：把符号“数字化”的数称为机器数
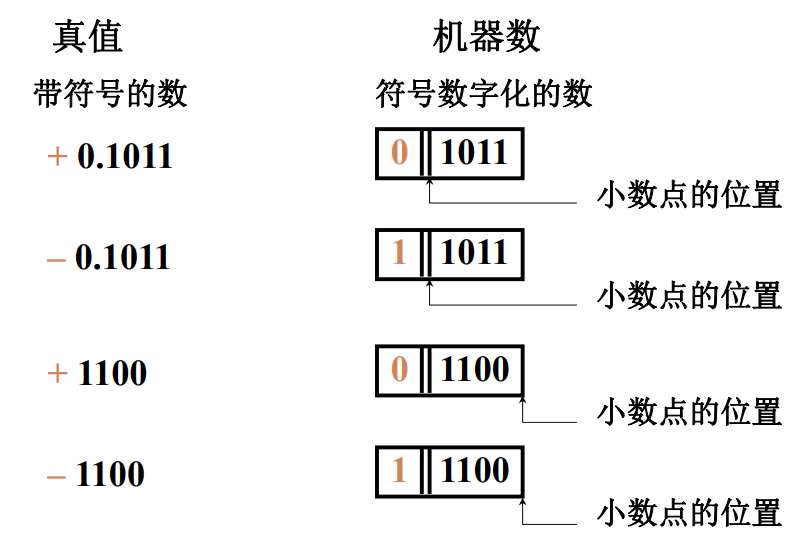
  • 真值：带+/-符号的数字 image.png

原码表示法

整数

\(\([x]_{原}= \left\{ \begin{matrix} 0,x \quad 2^{n}>x \geq 0 \\ 2^{n}-x \quad0 \geq x>-2^{n}\\ \end{matrix} \right.\)\) - 其中 - \(x\)为真值 - \(n\)为整数的位数 - 简单理解：在符号位上，使用0表示正，1表示负 - 举例： - \([+1110]_{\text{原}}=0,1110\) - \([-1110]_{原}=2^4-(-1110)=10000+1110=1,1110\)

我们使用\(,\)将符号位与数值部分分开

小数

\(\([x]_{原}= \left\{ \begin{matrix} x \quad 1>x \geq 0 \\ 1-x \quad 0 \geq x>-1 \\ \end{matrix} \right.\)\) - 公式中的\(1\)可以理解为符号负- - 举例： - \([0.1101]_原=0.1101\) - \([-0.1101]_原=1-(-0.1101)=1.0000+0.1101=1.1101\)

  • 原码的特点：
    • 简单直观
    • 缺点：
      • 做异号加法时候，需要进行比较大小，并且符号需要进行判断
      • 做减法？

补码

使用时钟的概念来理解补码，正拨与反拨效果一致

补的概念

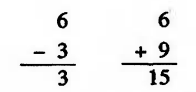
  • -3或+9最后在时钟上呈现的结果都是一致的——3点 image.png
  • 一个负数加上“模”即得到该负数的补数
    • 比如，在上例中，+9是-3以12为模的补数
  • 两个互为补数的数，其绝对值之和为模数

整数

\(\([x]_{补}= \left\{ \begin{matrix} 0,x\quad 2^{n}>x \geq 0 \\ 2^{n+1}+x \quad 0>x \geq -2^{n}(mod2^{n+1})\\ \end{matrix} \right.\)\) - 举例： - \([+1010]_补=0,1010\) - \([-1010]_补=100000-1010=1,0011\) - 一种求负数补码的快速方法：\([-x]_补=1,[\sim x+1]\) - 其绝对值取反+1 - 符号位为1

小数

\(\([x]_{补}= \left\{ \begin{matrix}x \quad 1>x \geq 0 \\ 2+x \quad 0>x \geq -1(mod2)\\ \end{matrix} \right.\)\) - 举例： - \([0.1001]_补=0.1001\) - \([-0.1001]_补=10+(-0.1001)=1.0111\)

一些特殊数的补码

  • \([-2^{n-1}]_补=100\dots0\)
  • \([-1]_补=111\dots1\)
  • \([-1.0]_补=1.00\dots0\)
  • \([+0]_补=[-0]_补=0.00\dots0\)

反码

取反 而 不加1 其他与补码一致

[!summary] - 最高位为符号位 - 对于正数，原码=补码=反码 - 对于负数，符号位为1，数值部分 - 补码=原码取反+1 - 反码=原码取反

[!attention] 原码、补码、反码对应的数据范围不同 image.png

移码

由于使用补码，很难直接判断其真值的大小，因此引入了补码

  • 移码与补码只相差一个符号位
    • \([0,1100100]_补=[1,1100100]_移\)
    • \([1,1100100]_补=[0,1100100]_移\)
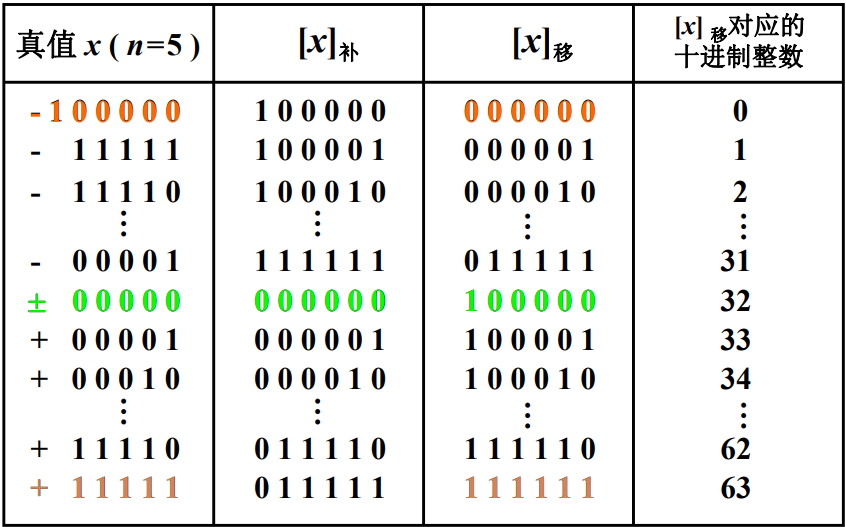
  • 对照表image.png

    对于后续的浮点数，使用移码来表示浮点数的阶码，能够更加方便的判断浮点数的阶码的大小