背包问题

01背包问题

f[i][j] 表示前i个物体，再体积为j情况下的总价值是多少 1. 不取第i个物品的情况：f[i][j] = f[i - 1][j]; 2. 取第i个物品的情况：f[i][j] = f[i - 1][j - v[i]];

最大价值：maxprice = max{i} 初始化：f[0][0] = 0;

//使用二维数组
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 1010;
int v[N], w[N], f[N][N];      //f数组表示i个物品，j体积下的最大价值

int main(){
    int n,m;
    cin >> n >> m;

    for(int i = 1;i <= n;i ++){
        scanf("%d%d", &v[i], &w[i]);
    }

    for(int i = 1;i <= n;i++){
        for(int j = 0;j <= m;j++){
            f[i][j] = f[i - 1][j];      //不放入的价值
            if(j >= v[i]){
                f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);      //比较放入与不放入的价值
            }
        }
    }

    cout <<f[n][m];

    return 0;
}

• 一维情况下的状态转移分析

• 转为一维情况下的逐步分析

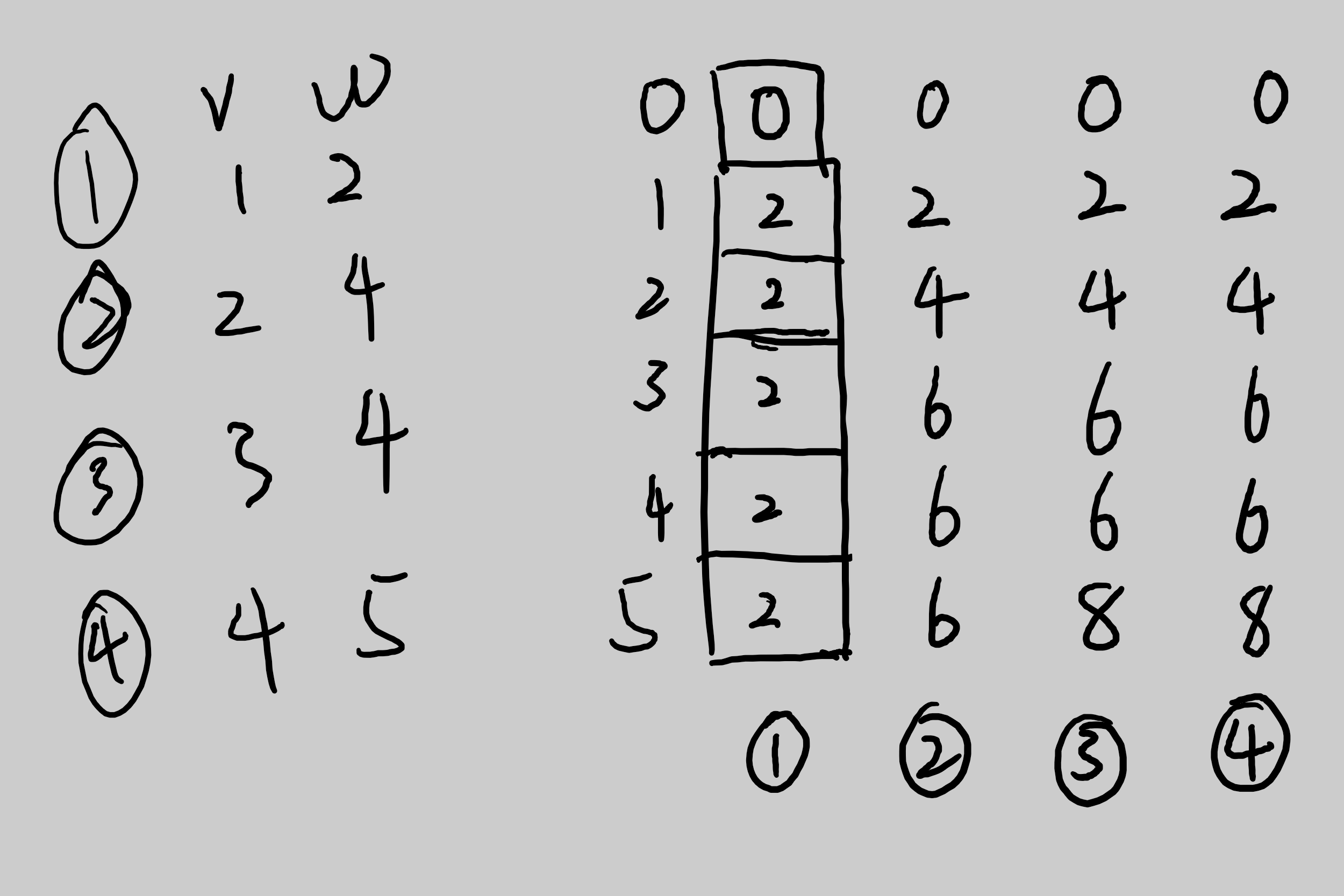
//使用一维数组d
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 1010;
int v[N], w[N], f[N];       //f数组表示j体积下的最大价值

int main(){
    int n,m;
    cin >> n >> m;

    for(int i = 1;i <= n;i ++){
        scanf("%d%d", &v[i], &w[i]);
    }

    for(int i = 1;i <= n;i++){
        for(int j = m;j >= v[i];j--){
                f[j] = max(f[j], f[j - v[i]] + w[i]);      //比较放入与不放入的价值

        }
    }


    cout <<f[m];

    return 0;
}

完全背包问题

• 有 N 种物品和一个容量是 V 的背包，每种物品都有无限件可用。

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;
int v[N], w[N];
int f[N][N];

int main(){
    int m, n;
    cin >> n >> m;
    for(int i = 1;i <= n;i++) cin >> v[i] >> w[i];


    for(int i = 1;i <= n;i++){
        for(int j = 0;j <= m;j++){
            f[i][j] = f[i - 1][j];
            if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
        }
    }

    cout << f[n][m];

    return 0;
}