关键路径

AOE网

1. 一个带权的有向无环图，顶点表示时间，弧表示活动，弧上的权值表示活动持续的时间
2. 实际工程问题：
   1. 估算完成整个工程至少需要多少时间
   2. 判断那些活动是关键活动

关键路径

1. 关键路径：源点->汇点的带权路径长度最大的路径称为关键路径，关键路径上的活动称为关键活动

关键路径的确定：

事件\(V_i\)的最早发生时间\(ve[i]\)

1. 事件发生的最早时间是从源点到\(V_i\)的最大路径长度
   • 最大：需要事件\(V_i\)的所有入边活动都已经完成，\(V_i\)才可以开始
2. 利用[[拓扑排序]]从源点向汇点递推，计算事件的最早发生时间
3. \(ve[i] =\max(V_e + W_{ei})\)

事件\(V_i\)的最晚发生时间\(vl[i]\)

1. 事件\(V_i\)的最迟发生时间不能影响其所有后继的最迟发生时间，即\(V_i\)的最迟发生时间减去活动\(a_{ik} = <V_i, V_k>\)的持续时间
2. 利用逆拓扑排序，从汇点向源点递推，求解事件的最迟发生时间
3. 初始化汇点的最迟发生时间为汇点的最早发生时间

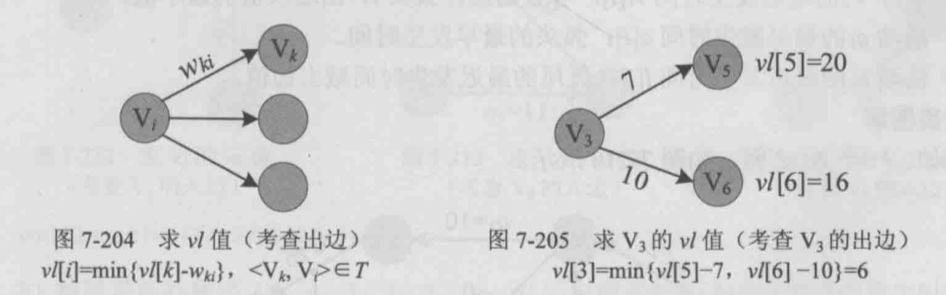
活动\(a_i = <V_j,V_k>\)的最早发生事件\(e[i]\)

• 事件\(V_j\)之后发生

活动\(a_i = <V_j,V_k>\)的最晚发生事件\(l[i]\)

• 活动\(a_i\)的最迟发生时间等于弧尾的最迟发生时间减去边值，\(l[i] = vl[k]-w_{jk}\)

算法步骤

1. 利用拓扑排序，将拓扑排序结果保存在\(topo[]\)
2. 将每个事件的最早发生时间初始化为0，
3. 根据拓扑顺序从前向后一次求每个事件的最早发生时间，循环执行以下操作
   1. 正序取出拓扑序列中的顶点\(k\)
   2. 依次处理\(k\)的每一个邻接点 （出） ，**更新顶点\(j\)的最早发生事件\(ve[j]\) if(ve[j] < ve[k] + p->weight) ve[j] = ve[k] + p->weight
4. 初始化事件的最晚发生时间
5. 根据逆拓扑排序从后向前，求解每个事件的最迟发生时间
   1. 逆序取出拓扑序列中的顶点
   2. 依次处理\(k\)的每个邻接点 （入），**更新顶点\(k\)的最迟发生时间\(vl[k]\) if(vl[k] > vl[j] - p->weight) vl[k] = vl[j] - p->weight
6. 求关键活动：若最早与最迟发生时间相同，则为关键活动