最小生成树
- 两种算法:Prim、Kruskal
- 优化:
- [[堆|普通二叉堆]]:\(O(E * \lg{V})\)
- [[斐波那契堆]]:Prim->\(O(E + V * \lg {V})\)
- 算法实质:贪心(最好的选择,但不保证能找到一个真正的全局最优)
- 通用方法:每个时刻生长最小生成树的一条边(即安全边)
- 同时遵守一个循环不变式的边集合A->在每一遍循环之前,A是某颗最小生成树的一个子集->选择一条边\((u,v)\),使得\(A\cup (u,v)\)也是某颗最小生成树的子集,这样的边称为==安全边==
- 使用循环不变式的方式
- 初始化:直接令集合A满足循环不变式
- 保持:不断加入安全边来保持循环不变式的成立
- 终止:无边可加之后,完成了某棵最小生成树的构造
Prim
找出\(n-1\)条权值最小且无回路的边即可
- 思路与[[Dijkstra]]基本相似,区别在于Prim将一整个集合看作源点,去寻找最短边
概念:
- [[基本术语#^e89c2f|子图]]
- [[基本术语#^e89c2f|生成子图]]
- [[基本术语#^c58be0|生成树]]
- [[基本术语#^c58be0|最小生成树]]
- 集合避圈法:在生成树的过程中,把已在生成树中的节点看作一个集合,把剩余的节点看作另一个集合,从连接两个集合中的边选择一条权值最小的边
- 实质:贪心->每一次加入的边总是权重最小的边
算法步骤
- 数据结构:邻接矩阵
G[u][v] = w / ∞,bool数组st[],用于标记是否加入集合\(U\),使用一个小根堆(优先队列)维护将两个集合连接的边的权重,利用其他结构存储相应的后继 - 初始化,将源点加入集合U,将源点的所有连接邻接点的边加入优先队列中,
- 不断加入最小的边,并注意维护循环不变式
- 图解
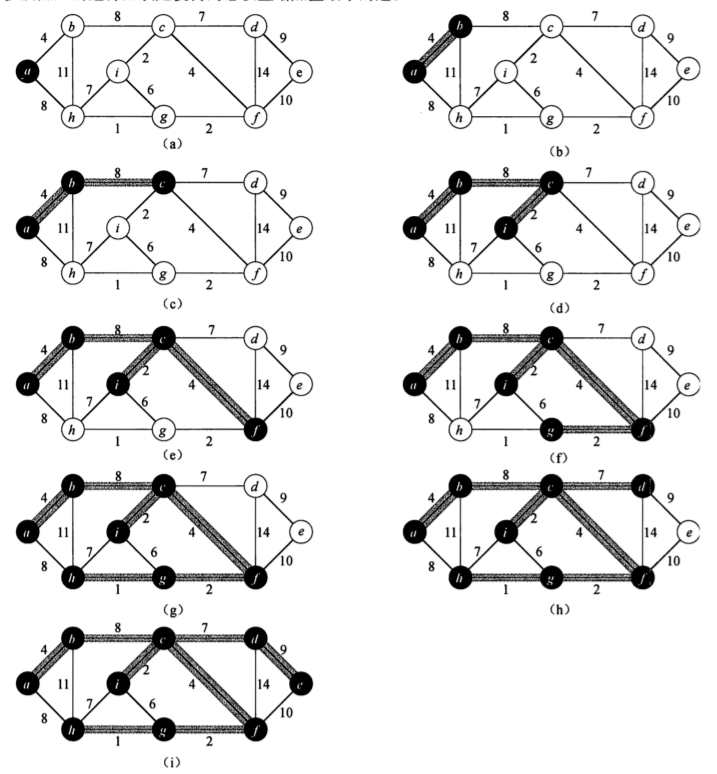
Kruskal
思路:
先将所有的边按照权重排序,接下来开始贪心:不断地选取最小且不会令集合中产生回路的边,如果产生回路,则不进行选取,继续贪心 - 如何判断加入边后不会产生回路? - 集合避圈:如果选择加入的起点和终点都在集合中,则一定会产生回路->边的两个节点不能属于同一个集合
算法步骤
- 初始化:将图中所有的边按从小到大顺序排序,每个顶点独立成为一个集合
- 找权值最小的边\((i,j)\)
- 如果\(i,j\)连接不同的分支,则对边\((i,j)\)执行合并操作
- 如果选取的边数\(\le n-1\),则重复进行2、3
- 图解:
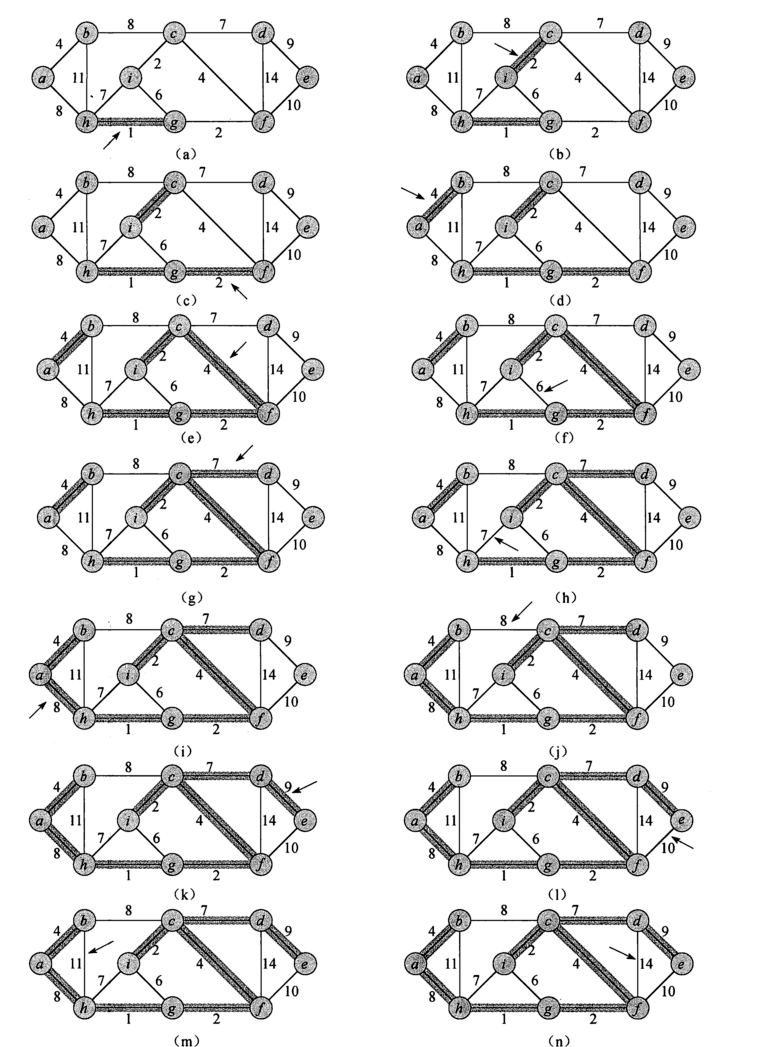
算法优化
- 时间优化:
- 更快的排序算法
- 使用堆存储边的权值
- 使用[[并查集]]合并集合