树表查找

二叉查找树(BST)

性质(左子树<根<右子树)

若左子树非空，则左子树上所有结点的值均小于根节点的值
若右子树非空，则右子树上所有节点的值均大于根节点的值
其左右子树本身又是一棵二叉查找树
二叉查找树的中序遍历是递增序列

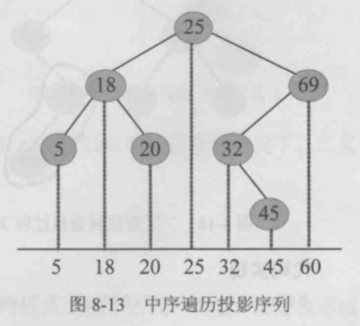
应用

查找、排序

基本操作

查找

基本思路：利用二叉查找树的[[树表查找#性质左子树根右子树|性质]]
1. 如果当前结点为空：查找失败
2. 如果当前结点的值大于x：递归或迭代左子树
3. 如果当前结点的值小于x：递归或迭代右子树
4. 相等：查找成功！！
时间复杂度：\(O(h)\) h是二叉查找树的高度

代码：

public bool search(T num){
    BiNode<T>* node = root;
    if(root == NULL) return false;
    else{
        if(node->data == num) return true;
        else if(node->data > num) return searchin(node->lchild, num);
        else return searchin(node->rchild, num);
    }
}

private bool searchin(BiNode<T>* node, T num){
    if(node->data == num) return true;
    else if(node->data > num) return searchin(node->lchild, num);
    else return searchin(node->rchild, num);
}

插入

基本思路：利用查找
1. 如果查找成功，不插入
2. 查找失败，在空结点时新建需要插入的结点
时间复杂度：\(O(h)\) h是二叉查找树的高度
代码：

bool insert(T num){
    return insertin(root, num);
}
bool insertin(BiNode<T>* &node, T num){     //对lchild的指针的引用，可以直接修改lchild的地址
    if(node == NULL){
        BiNode<T>* newnode = new BiNode<T>;
        newnode->data = num;
        node = newnode;
        return true;
    }
    if(node->data == num){
        return false;
    }
    else if(node->data > num) return insertin(node->lchild, num);
    else return insertin(node->rchild, num);
}

建树

基本思路：建树即为不断插入的过程
注意：以不同的顺序插入同一组数字，最后生成的二叉查找树可能不同
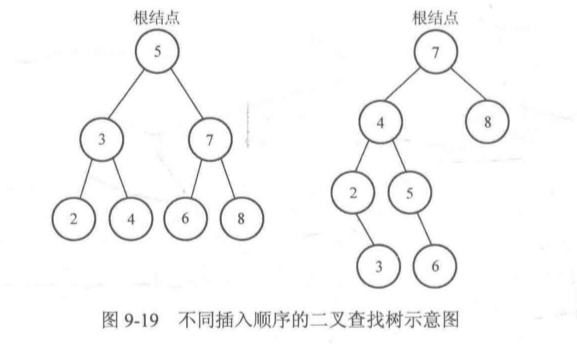
代码：

void create(T num[], int n){
    for(int i = 0;i < n;i++){
        insert(num[i]);
    }
}

删除

基本思路：
1. 无子树：直接删除
2. 存在左子树：令左子树替代其位置
3. 存在右子树：令右子树替代其位置
4. 左右子树都存在：用直接前驱（或直接后继）替代其位置，再删除其直接前驱（直接后继）
  - 直接前驱查找：中序遍历中，结点p的直接前驱为左子树的最右结点
  - 直接后继查找：中序遍历中，结点p的直接后继为右子树的最左节点
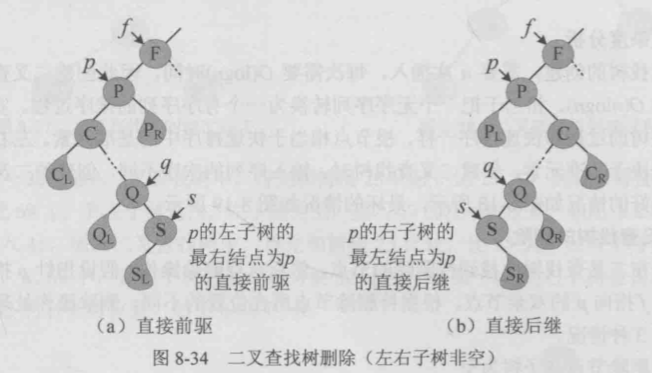
时间复杂度：\(O(\log{n})\)
代码：

bool remove(T num){
    return remove(root, num);
}
bool remove(BiNode<T>* &node, T num){
    if(node == NULL) return false;
    if(node->data > num) return remove(node->lchild, num);
    else if(node->data < num) return remove(node->rchild, num);
    else{
        if(!(node->rchild) && !(node->lchild)) {node = NULL; return true;}    //左右子树并不存在
        else if(node->lchild){
            BiNode<T>* alternode = node->lchild;
            while(alternode->rchild) alternode = alternode->rchild;     //寻找左子树的最有子树（直接前驱）
            node->data = alternode->data;
            return remove(node->lchild, alternode->data);
        }
        else if(node->rchild){
            BiNode<T>* alternode = node->rchild;
            while(alternode->lchild) alternode = alternode->lchild;
            node->data = alternode->data;
            return remove(node->rchild, alternode->data);
        }
    }
    return false;
}

平衡二叉查找树(AVL树)

对于二叉查找树来说，时间复杂度取决于树的高度，因此，通过一个平衡的操作，使二叉查找数能够最大程度上利用，降低查找的时间复杂度

性质：

平衡因子：左右子树的高度差
左右子树的高度差绝对值不超过1
左右子树也是平衡二叉树
单次插入删除后，至多有\(O(1)\)处出现不平衡
总可以在\(O(\log{n})\)时间内，使\(O(1)\)除不平衡重新调整为平衡

调整平衡的方法

插入新结点或删除结点x后，从该节点向上找到最近的不平衡结点A，以下型针对路径区分
插入结点只需要重平衡一次
删除则至少一次（向树根传递）

LL型

路径的前两个都是左子树，即为LL型（x插入在A的左子树的左子树，导致了结点A不平衡）
LL旋转：

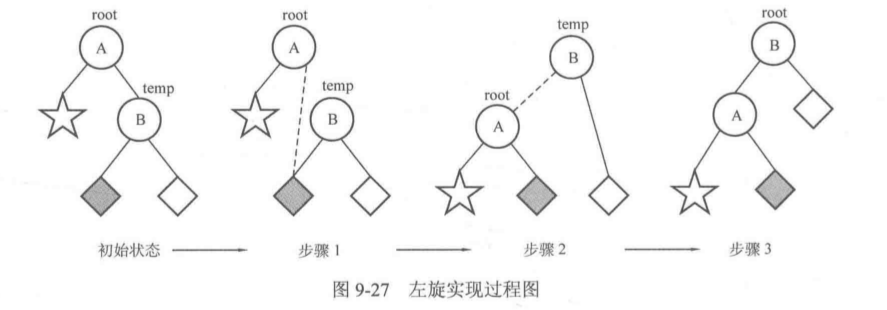
代码：

BiNode<T> LL_Rotation(BiNode<T> &T){
    BiNode<T> temp = T->lchild;
    T->lchild = temp->rchild;
    temp->rchild = T;
    updataHeight(T);
    updateHeight(temp);
    return temp;
}

RR型

路径的前两个都是右子树，即为RR型
RR旋转：

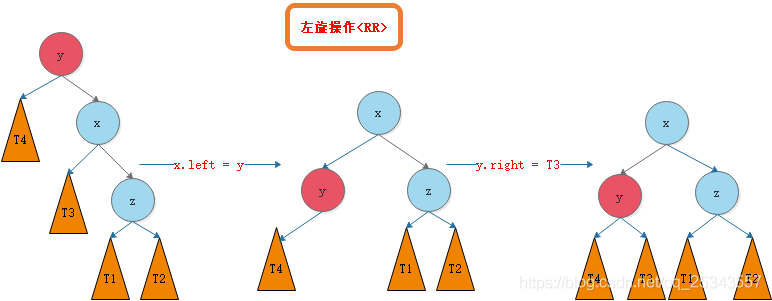
代码：

BiNode<T> RR_Rotation(BiNode<T> &T){
    BiNode<T> temp = T->rchild;
    T->rchild = temp->lchild;
    temp->lchild = T;
    updateHeight(T);
    update(temp);
    return temp;
}

LR型

路径的前两个子树依次是左子树、右子树，即为LR型
LR旋转：分为两次旋转：

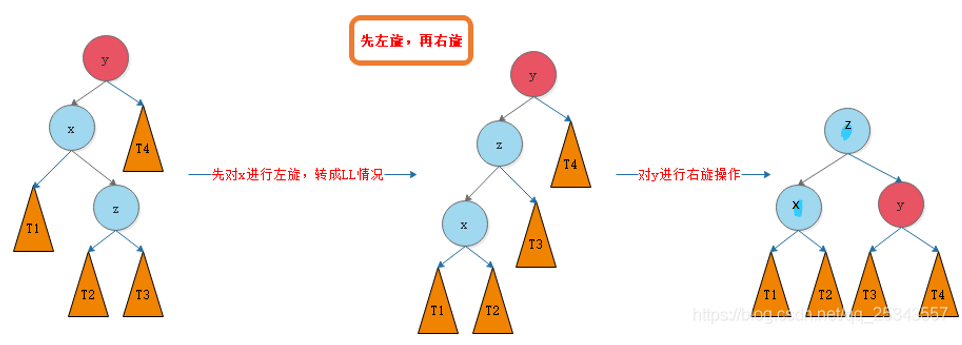
代码：

BiNode<T> LR_Rotation(BiNode<T> &T){
    T->lchild = RR_Rotation(T->lchild);
    return LL_Rotation(T);
}

RL型

路径的前两个子树依次是右子树、左子树，即为RL型
RL旋转：同分为两次旋转

树表查找

二叉查找树(BST)

性质(左子树<根<右子树)

应用

基本操作

查找

插入

建树

删除

平衡二叉查找树(AVL树)

性质：

调整平衡的方法

LL型

RR型

LR型

RL型

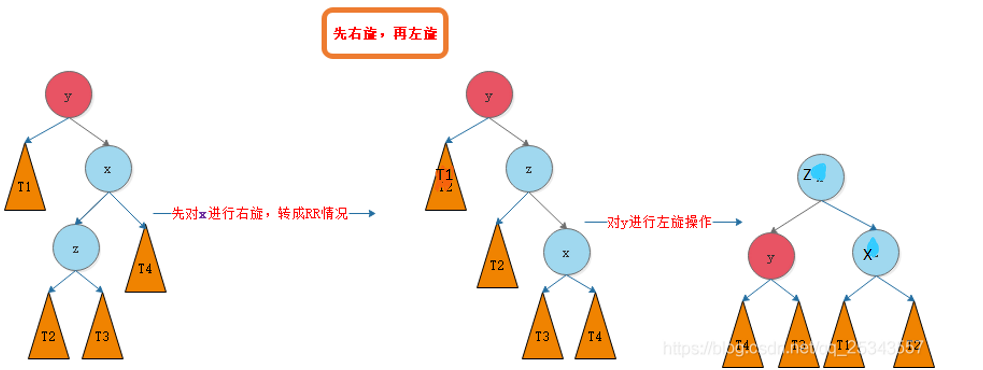
如何判断？？？