跳转至

正规表达式与有限自动机

![[高级语言及其语法描述#基本概念的介绍]]

正规式与正规集

  • 正规集可以使用正规表达式表示
  • 正规表达式是表示正规集的一种方法
  • 一个字集合是正规集当且仅当它能用正规式表示

  • 正规式与正规集的递归定义：

    • 对于给定的字母表\(\Sigma\)
      • \(\varepsilon\)和\(\varnothing\)都是\(\Sigma\)上的正规式，其表示的正规集为\(\{\varepsilon\}\)和\(\varnothing\)
      • 对于任何\(a\in\Sigma\)，\(a\)是\(\Sigma\)上的正规式，其表示的正规集为\(\{a\}\)
      • 如果\(e_1\)和\(e_2\)都是\(\Sigma\)上的正规式，他们所表示的正规集为\(L(e_1)\)和\(L(e_2)\)，则
        • \((e_1|e_2)\)为正规式，其表示的正规集为\(L(e_1)\cup L(e_2)\)
        • \((e_1\cdot e_2)\)为正规式，其表示的正规集为\(L(e_1)L(e_2)\)
        • \((e_1)^*\)为正规式，其表示的正规集为\((L(e_1))^*\)

          仅由有限次使用上述三步骤而定义的表达式才是\(\Sigma\)上的正规式，仅由这些正规式表示的正规集才是\(\Sigma\)上的正规集

  • 所有词法结构一般都可以使用正规式描述

  • 若两个正规式所表示的正规集相同，则称这两个正规式等价：
    • \(b(ab)^*=(ba)^*b\)image.png
    • \((a^*b^*)^*=(a|b)^*\)
  • 对于正规式，下列等价成立：
    • 交换律：\(e_1|e_2=e_2|e_1\)
    • 结合律：
      • \(e_1|(e_2|e_3)=(e_1|e_2)|e_3\)
      • \(e_1(e_2e_3)=(e_1e_2)e_3\)
    • 分配律：
      • \(e_1(e_2|e_3)=e_1e_2|e_1e_3\)
      • \((e_2|e_3)e_1=e_2e_1|e_3e_1\)

确定有限自动机(DFA)

  • 自动机M是一个五元式\(M=(S,\Sigma,f,S_0,F)\)
    • 有穷状态集\(S\)
    • 输入字母表\(\Sigma\)
    • 状态转换函数\(f\)
    • 唯一一个初态\(S_0\in S\)
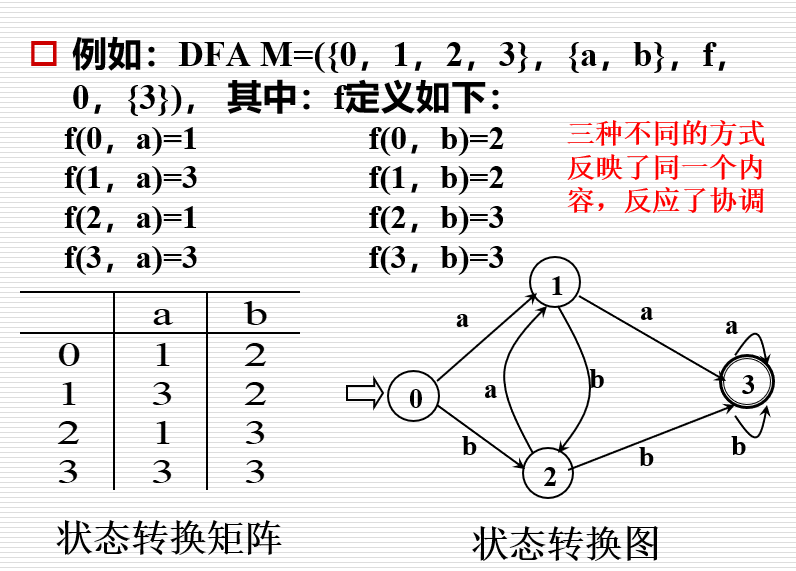
    • 终态集（可空）\(F\subseteq S\)image.png
  • DFA可以表示为状态转换图
  • 对于\(\Sigma^*\)中的任何字\(\alpha\)，若存在一条从初态到某一终态的道路，且道路上所有弧上的标记符连成的字为\(\alpha\)，则称\(\alpha\)为DFA M所识别
  • DFA M所识别的全体字称为\(L(M)\)

    \(\Sigma\)上的字集\(V\subseteq \Sigma^*\)是正规集，当且仅当存在\(\Sigma\)上的DFA M，使得\(V=L(M)\)

非确定有限自动机(NFA)

  • 与DFA的区别：
    • 弧上的标记可以是\(\Sigma^*\)的一个字，而不一定是单个字符
    • 同一个字可能出现在同状态射出的多条弧上

  • 编译原理重点 DFA与NFA的描述能力相同：对于每个NFA M存在一个DFA M'，使得L(M)=L(M')

    image.png

正规文法与有限自动机的等价性

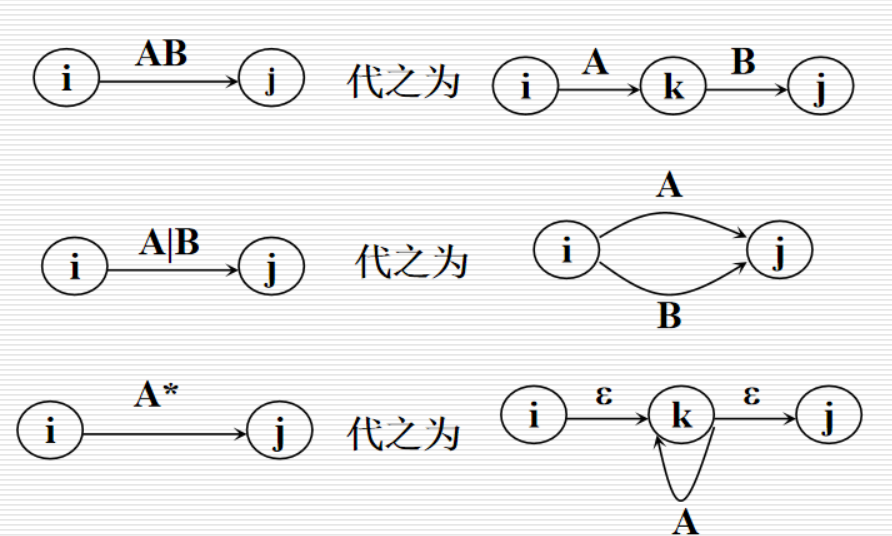
正规式与有限自动机的等价性

  • 定理：
    • 任何(FA)M，有存在一个正规式\(r\)，使\(L(r)=L(M)\)
    • 对于任何正规式\(r\)，都存在一个FA(M)，使\(L(r)=L(M)\)