跳转至

自底向上的语法分析

  • 基本思想：
    • 从输入串开始，逐步进行“[[自底向上的语法分析#归约|归约]]"，直到文法的开始符号
    • 从语法树的角度来看：从语法树的树叶开始，逐步向上归约构造分析树，直到形成根节点。 归约.gif

      归约可以理解为推导的逆过程

归约

  • 采用移进——归约的思想进行自下而上的分析
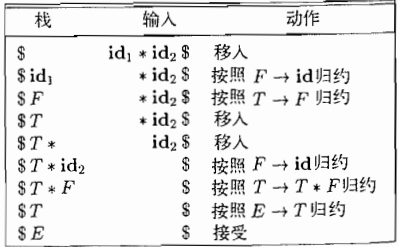
    • 基本思想：从输入符号串开始，从左到右进行扫描，将输入符号逐个移入一个栈中，边移入边分析，一旦栈顶符号串形成某个产生式的右部时，则进行归约。重复这一过程，直到归约到栈中只剩下文法的开始符号
  • 归约：一个与某产生式体相匹配的特定子串被替换为该产生式头部的非终结符 归约示例.gif image.png

#编译原理重点 规范归约

\(\(S\stackrel{*}{\Rightarrow}\alpha A\delta \quad\&\& \quad A\stackrel{+}{\Rightarrow}\beta\)\) - 短语：\(\beta\)是句型\(\alpha\beta\delta\)相对于非终结符\(A\)的短语 - 直接短语：如果有\(A\Rightarrow\beta\)，则称\(\beta\)是句型\(\alpha\beta\delta\)的相对于规则\(A\rightarrow\beta\)的直接短语（可直接推导） - 一个句型的最左直接短语称为该句型的句柄 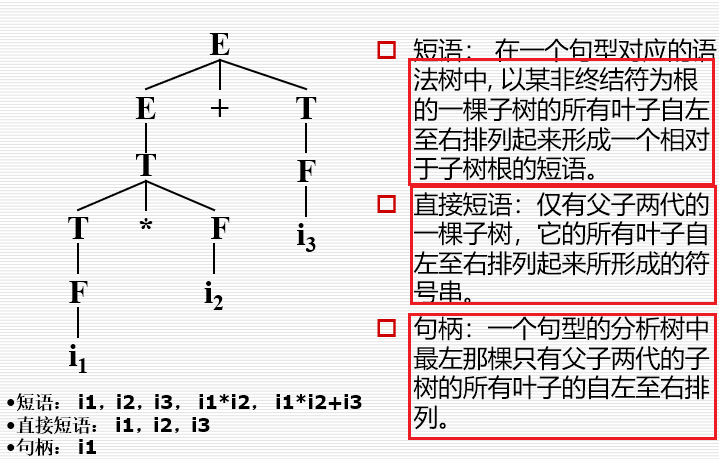image.png image.png - 短语、直接短语和句柄的判断，根据树来判断更加方便。 image.png - 规范归约是一个最右推导的逆过程

符号栈的使用和分析树的表示

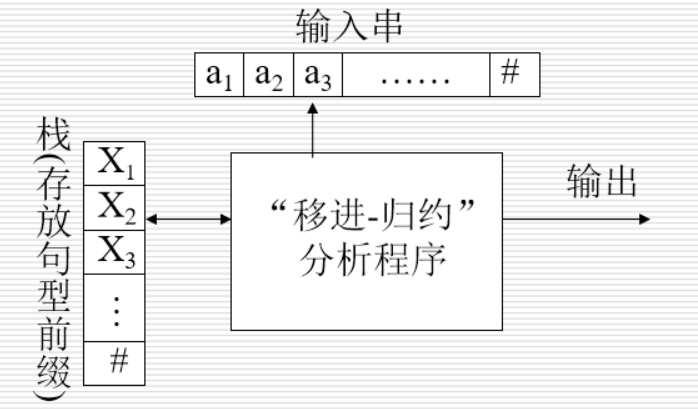
  1. 句型表示：分析栈内容+输入缓冲区内容=#当前句型#image.png
  2. 分析器结构image.png

句柄剪枝

  • 句柄：是和某个产生式体匹配的子串，对其的归约操作代表了相应的最右推导中的一个反向步骤
  • 如果有最右推导：\(S \stackrel{*}{\underset{r m}{\Rightarrow}} \alpha A w \underset{rm}{\Rightarrow} \alpha \beta w\)，那么紧跟在\(\alpha\)后的产生式\(A\rightarrow \beta\)是\(\alpha A w\)的一个句柄
    • 换句话说：最右句型\(\gamma\)的一个句柄是满足下述条件的产生式\(A\rightarrow \beta\)及串在\(\gamma\)中出现的位置：
      • 将这个位置上的\(\beta\)替换为\(A\)之后的得到串是\(\gamma\)的某个最右推导序列中出现在位于\(\gamma\)之前的最右句型
  • 句柄右边的串\(w\)一定只包含终结符号
  • 我们仅在句柄上进行归约操作，而不是单纯的根据产生式
  • 如果文法是二义性的，可能存在多个句柄

    [!note] 通过“句柄剪枝”，我们可以得到一个反向的最右推导。即，如果\(w\)是当前文法要得到的句子，那么令\(w=\gamma_n\)（\(\gamma_n\)是某个位置最右推导的第n个最右句型） \(\(S=\gamma_0\Rightarrow\gamma_1\Rightarrow\gamma_2\Rightarrow\dots\Rightarrow\gamma_{n-1}\Rightarrow\gamma_n=w\)\) 为了以相反的顺序重构这个推导过程，我们需要在\(\gamma_n\)中寻找句柄\(\beta\)，并且根据产生式将其替换，得到前一个最右句型\(\gamma_{n-1}\)，如此反复，最后就能得到一个只包含开始符号的最右句型。 将归约过程中用到的产生式反向排序，就得到了输入串的一个最右推导过程。

移入——归约语法分析技术

  • 移入归约语法分析技术使自底向上语法分析的一种形式：
    • 符号栈：使用一个栈来保存文法符号
      • 使用一个不属于文法符号的\(\#\)作为栈底符号
    • 输入缓冲区：存放将要进行语法分析的其余符号
      • 使用\(\$\)作为句子的结束符
  • 在开始时，栈为空，输入串\(w\)存放在输入缓冲区中image.png
  • 在扫描的过程中，语法分析器每次将零个或多个符号移动到栈的顶部，直到对其栈顶的文法符号串\(\beta\)可以进行归约
    • 语法分析器不断重复这个操作，直到遇到了错误
  • 移入——归约语法分析器的四种实际动作：
    • 移入(shift)：将下一个输入符号移动到栈顶
    • 归约(reduce)：
      • 被归约的符号串右端必须是栈顶
      • 语法分析器在栈中确定这个串的左端，并且决定使用哪一个非终结符来替换这个串
    • 接受(accept)：确定语法分析完成
    • 报错(error)：发现语法错误 image.png