跳转至

LR分析法

  • 编译原理重点 LR

    • L：表示从左向右扫描输入串
    • R：构造最右推导的逆过程
  • 大多数使用上下文无关文法描述的高级语言的语法成分都可以使用LR分析器来识别
  • LR分析根据当前分析栈中的符号串和向右顺序查看输入串的K（LR(K)）个符号就可以唯一确定分析的动作是移进还是归约
  • 关键问题：如何确定可归约的串？
    • 解决方案：通过求句柄，逐步归约
    • 如何求得句柄？
      • 在算符优先分析中，是通过算符的优先关系求得
      • 在LR方法中，是通过活前缀求得

LR分析器

  • 核心问题：寻找句柄

  • 编译原理重点 基本思想：在规范归约的过程中，一方面记住已经移进和归约出的整个符号串（历史），另一方面有根据所用产生式来推测未来可能碰到的输入符号（未来）

    • 现实：当前的输入符号
    • 当某一符号串类似于句柄出现在栈顶时，需要根据历史、展望和现实来决定栈顶的符号串是否构成一个句柄，是否需要归约

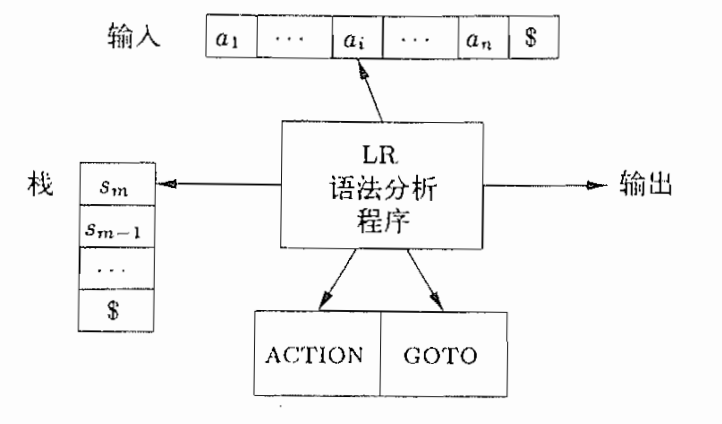
  • 编译原理重点 LR分析器的结构：image.png

    • 栈：用来存放状态
      • 符号栈
      • 状态栈
    • 分析表：是一个带有先进后出栈的确定的有穷自动机。用于将历史与展望综合成状态
      • 包括了：
        • ACTION[s,a]表：当状态\(s\)在面临输入符号\(a\)时，应该采取什么动作
        • GOTO[s,X]表：当状态\(s\)面临文法符号\(X\)时，下一个状态是什么

          利用栈与分析表，我们就可以根据栈顶状态和输入符号，唯一的确定下一个动作

  • 编译原理重点 ACTION[s,a]中的四种动作：

    • 移进(s)：把(s,a)的下一状态\(s^\prime\)和输入符号推进栈，下一个输入符号变成现输入符号
    • 归约(r)：使用产生式\(A\rightarrow \beta\)进行归约，状态\(s_{m-r}\)成为新的栈顶，然后把\((s_{m-r},A)\)的下一个状态\(s^\prime=GOTO[s_{m-r}, A]\)和文法符号\(A\)推进栈
    • 接收(acc)：宣布结束
    • 报错()
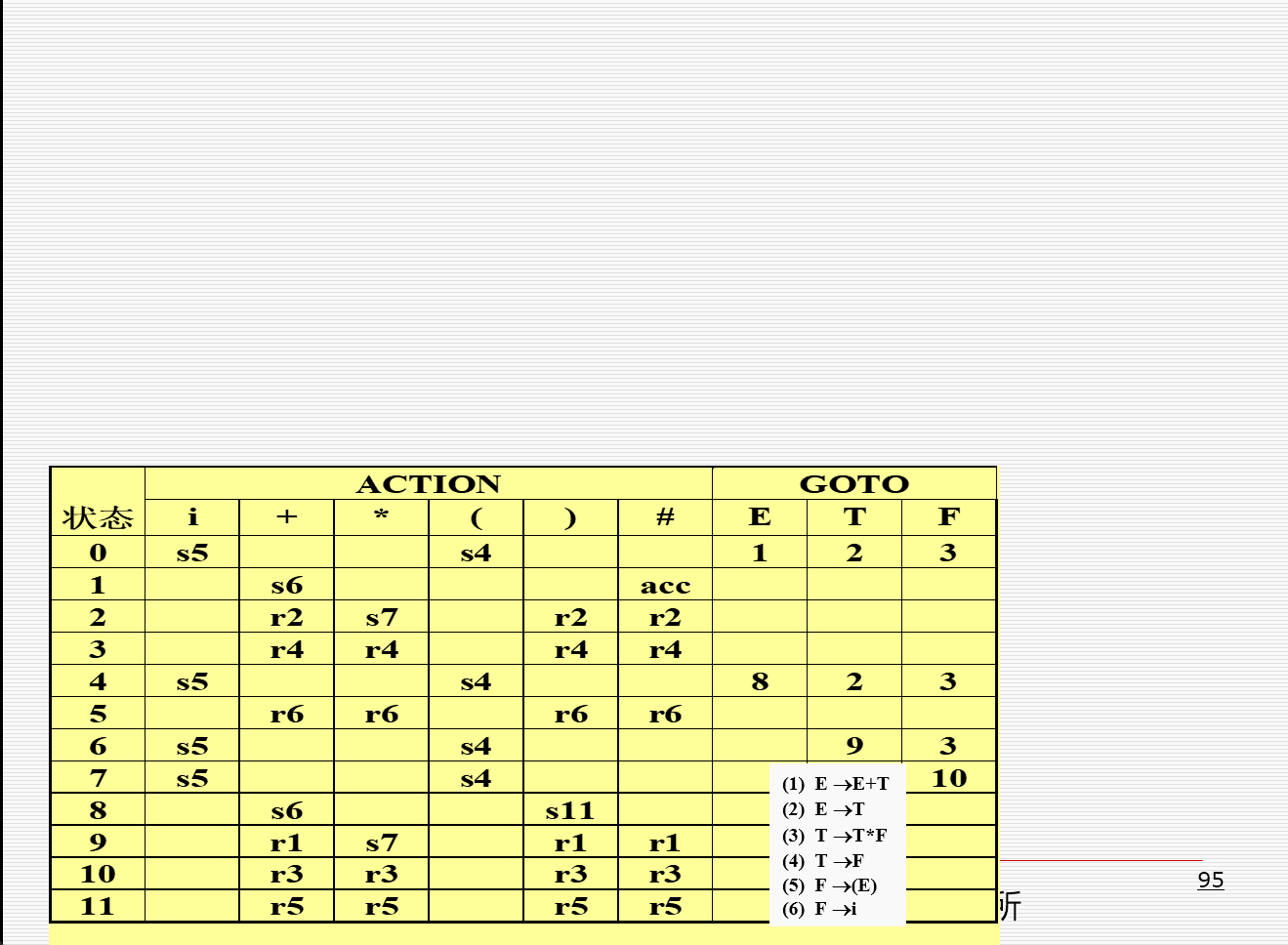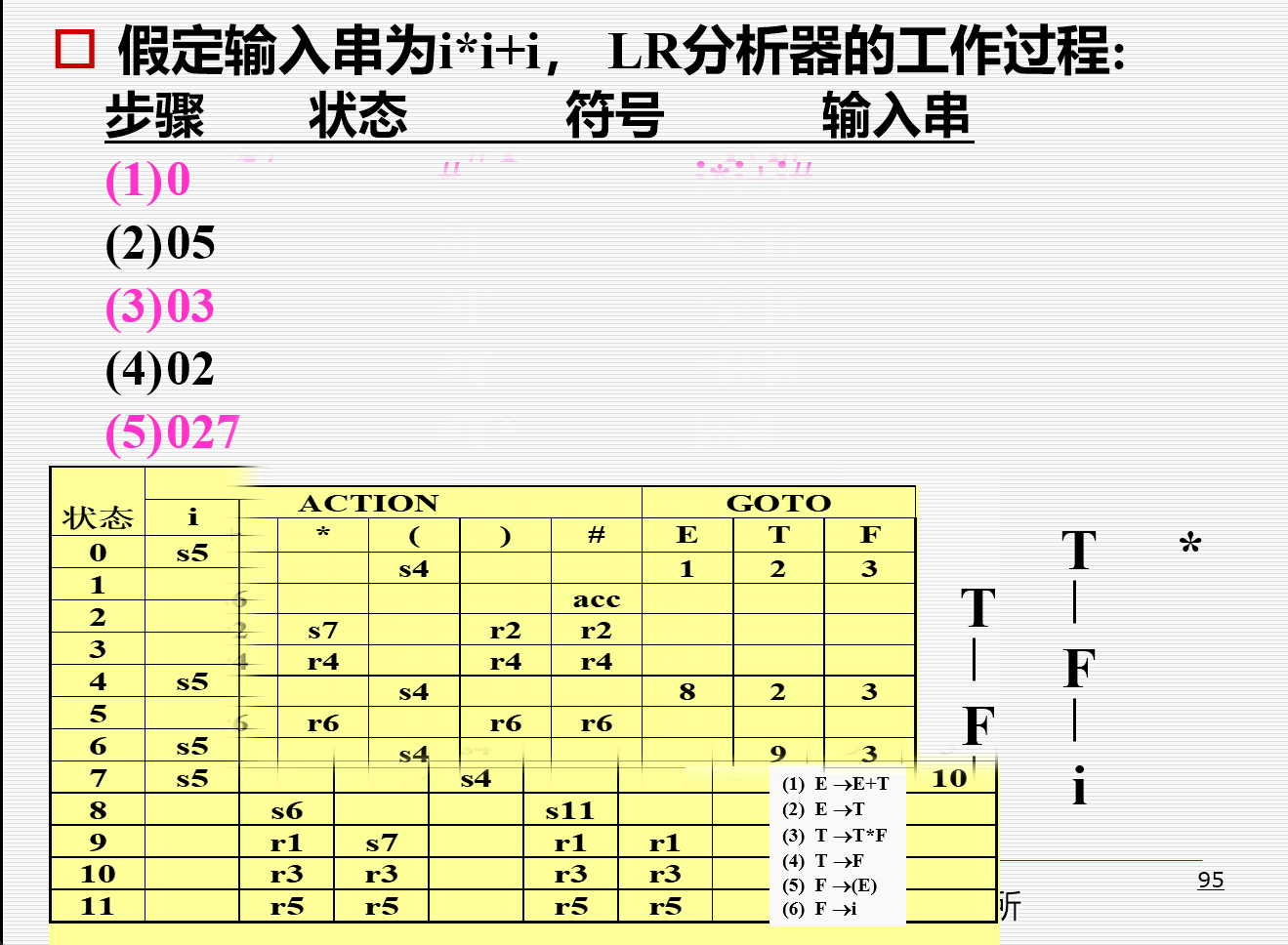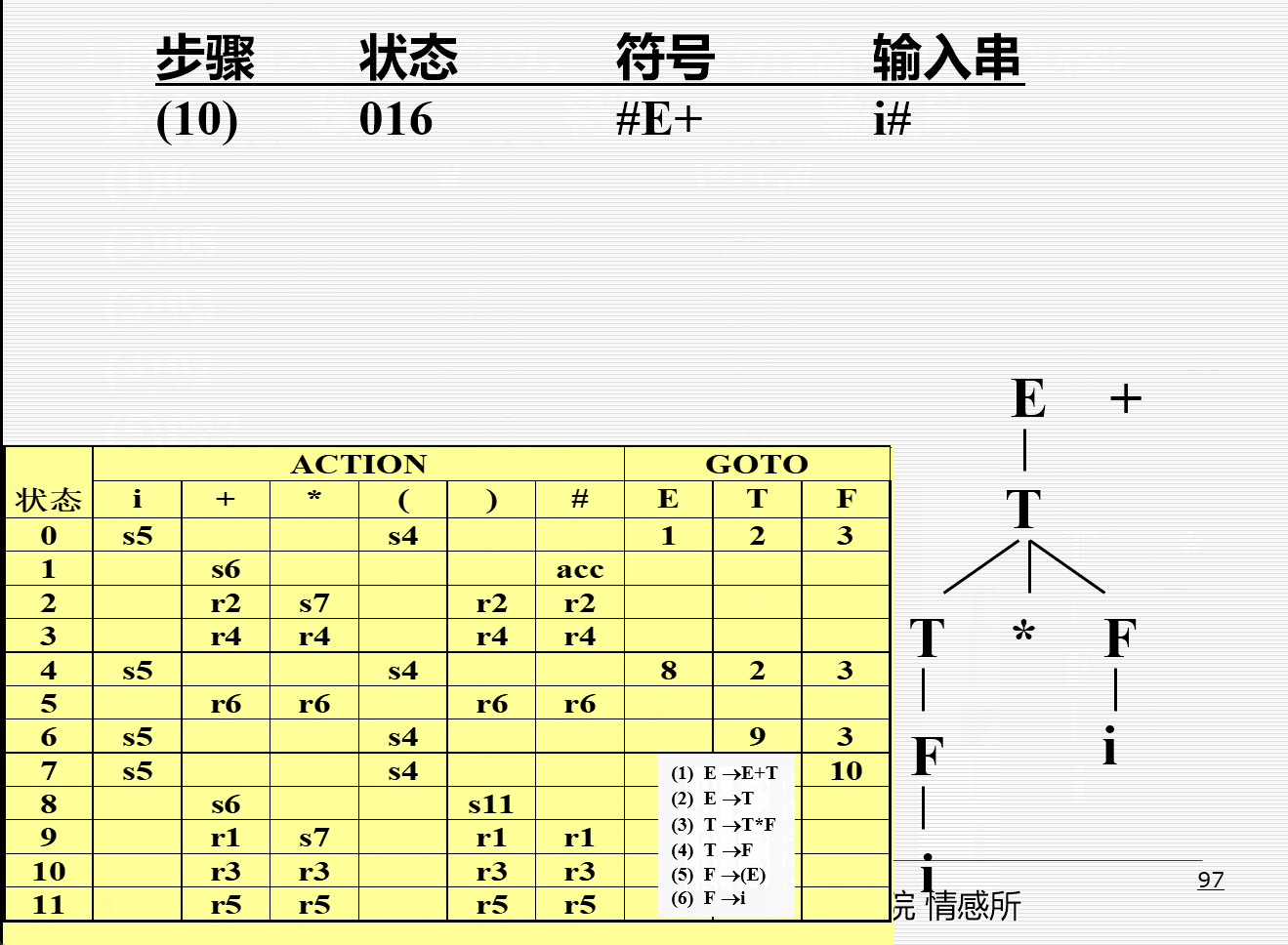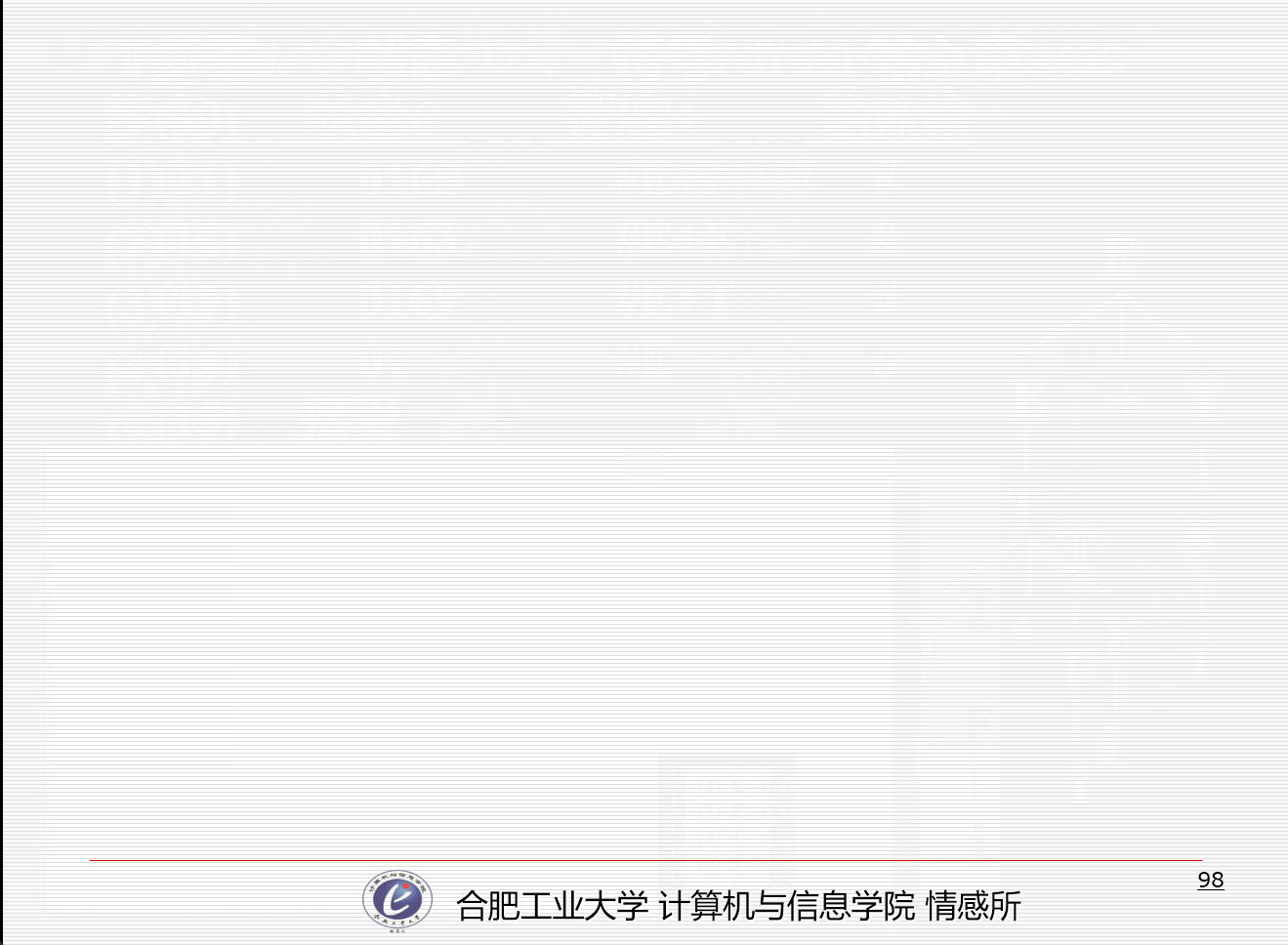
  • 一个分析示例：LR_example.gif (1319×968) (raw.githubusercontent.com)

LR文法

  • LR文法：对于一个文法，如果能够构造一张分析表，使得它的每个入口均是唯一确定的，则这个文法就称为LR文法
    • LR文法一定是无二义性的
  • LR(k)文法：对于一个文法，如果能用一个每步顶多向前检查k个输入符号的LR分析器进行分析，则称为LR(k)文法
    • 对于多数的程序语言来说，k=0/1即足够

项与LR(0)分析表的构造

  • 规范归约：如果\(\alpha\)是文法G的一个句子，则称序列\(\alpha_n, \alpha_{n-1}, \dots,\alpha_{1}, \alpha_0\)是一个规范归约
    • 满足：
      • \(\alpha_n = \alpha\)
      • \(\alpha_0 = 开始符号\)
      • \(\alpha_{i-1}\)是\(\alpha_i\)经过把句柄替换为相应产生式左部符号而得
  • 在规范归约的过程中：
    • 栈内的符号串和扫描剩下的输入符号串构成了一个规范句型
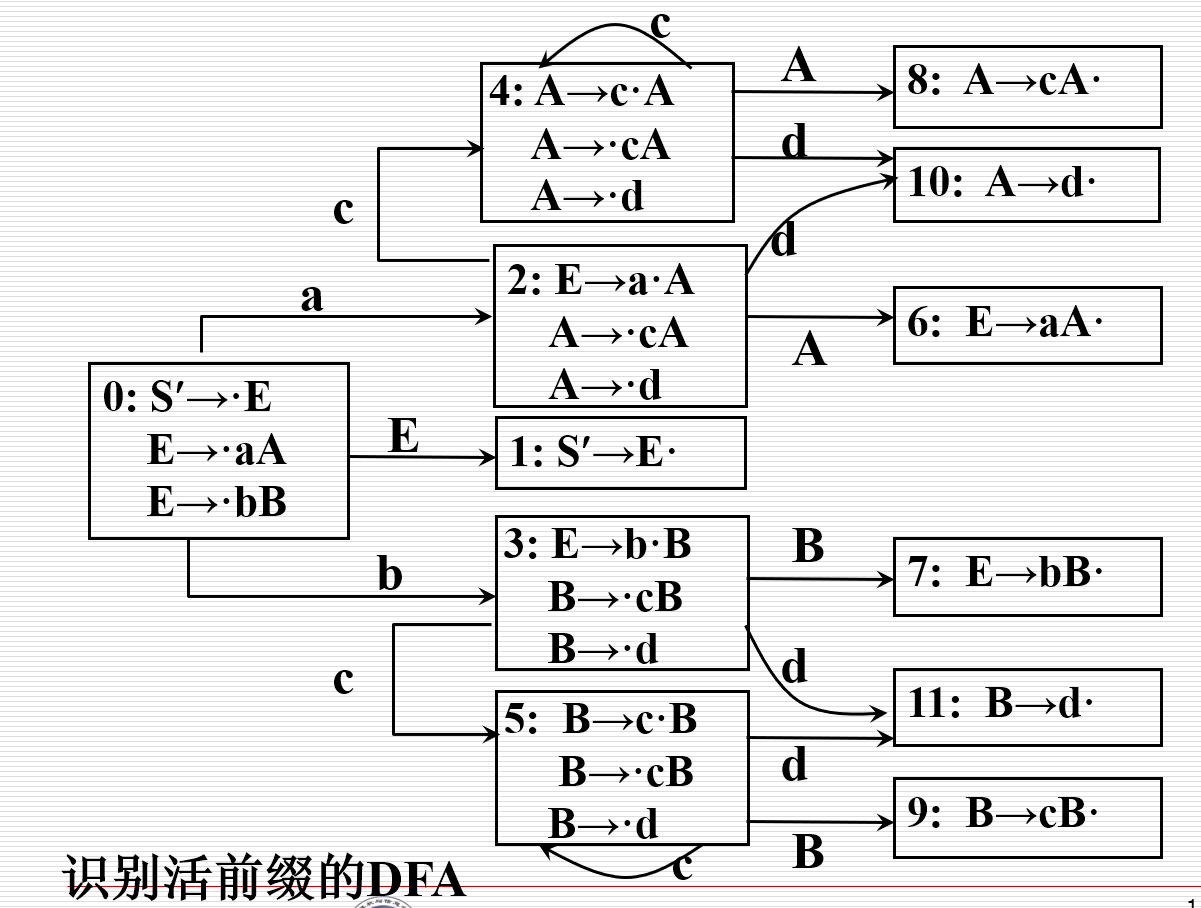
    • 栈内如果出现句柄，则该句柄一定在栈顶image.png

  • 编译原理重点 对于LR(0)分析法，语法分析栈中存放的状态是识别规范句型活前缀的DFA状态

活前缀

  • 字的前缀：指字的任意首部
    • abc的前缀：\(\varepsilon\)、a、ab、abc

  • 编译原理重点 活前缀：指规范句型的一个前缀

    • 这样的前缀不包含句柄之后的任何符号
    • 对于规范句型\(\alpha \beta \delta\)，其中\(\beta\)为句柄，则在\(\beta\)之前（包括\(\beta\)）都可以称为\(\alpha\beta\delta\)的活前缀，\(\delta\)为终结符串
  • 对于一个文法G，可以构造一个DFA，它能够识别G的所有活前缀
  • 识别活前缀的本质就是识别句柄
    • 活前缀与句柄的关系：
      • 活前缀已含有句柄的全部符号：表明该句柄对应的产生式\(A\rightarrow \alpha\)的右部\(\alpha\)已经出现在栈顶，此时可以进行归约操作，该活前缀称为可归约活前缀
      • 活前缀只含句柄的一部分：表明在句柄对应的产生式\(A\rightarrow \alpha 1\alpha 2\)的右部子串\(\alpha1\)已经出现在栈顶，期待从输入串中看到\(\alpha2\)推导出的字符串
      • 活前缀不含有句柄的任何符号：此时期待从输入串中看到该句柄对应的产生式\(A\rightarrow\alpha\)的右部所推出的符号串
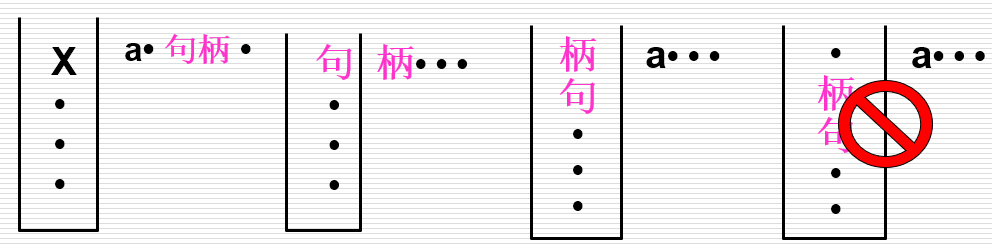
  • 活前缀的识别示例：对于文法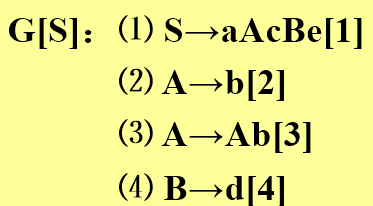image.png，识别一个输入串abbcde：
    • 最右推导顺序：\(S\rightarrow aAcBe[1] \rightarrow aAcd[4]e[1] \rightarrow aAb[3]cd[4]e[1] \rightarrow ab[2]b[3]cd[4]e[1]\)

    • 编译原理重点 规范句型及其活前缀：

      • \(abbcde\)：\(\varepsilon, a, ab\)
      • \(aAbcde\)：\(\varepsilon, a, aA, aAb\)
      • \(aAcde\)：\(\varepsilon, a, aA, aAc, aAcd\)
      • \(aAcBe\)：\(\varepsilon, a, aA, aAc, aAcB, aAcBe\)

构造自动机识别活前缀

对于一个文法G，我们可以构造一个有限自动机，它能够识别G的所有活前缀 由于产生式右部的符号就是句柄，若这些符号串都已经进栈，则表示它已处于“归态活前缀”，若只有部分进栈，则为“非归态活前缀” 要想知道活前缀有多大部分进栈了，我们可以为每个产生式构造一个自动机，由它的状态记住这些情况，此"状态"称为“项目”。 这些自动机的全体就是识别所有活前缀的有限自动机。 - 项目：文法G的每个产生式右部添加一个圆点，称为G的LR(0)项目 - \(A\rightarrow XYZ\)的项目： - \(A\rightarrow\cdot XYZ\) - 表明我们希望接下来在输入中看到一个从\(XYZ\)推导得到的串 - \(A\rightarrow X\cdot YZ\) - 说明我们刚刚在输入中看到了一个可以由\(X\)推导得到的串，并且我们接下来希望能够看到一个可以由\(YZ\)推导得到的串 - \(A\rightarrow XY\cdot Z\) - \(A\rightarrow XYZ\cdot\) - 其中，\(A\rightarrow \alpha\cdot\)称为归约项目 - image.png - 项目的表示：使用一对整数表示 - 第一个整数代表产生式编号 - 第二个整数表示圆点的位置 - 构造识别文法所有活前缀的NFA方法image.png 1. 若状态\(i\)为\(X\rightarrow X_1\cdots X_{i-1}\cdot X_{i}\cdots X_n\)，状态\(j\)为\(X\rightarrow X_1\cdots X_{i-1} X_{i}\cdot X_{i +1}\cdots X_n\)，则从状态\(i\)画一条标志为\(X_i\)的有向边到状态\(j\) 2. 若状态\(i\)为\(X\rightarrow\alpha\cdot A\beta\)，\(A\)为非终结符，则从\(i\)画一条\(\varepsilon\)边到所有状态\(A\rightarrow\cdot\gamma\) - 通过确定化的操作，将NFA转换为DFAimage.png

有效项目

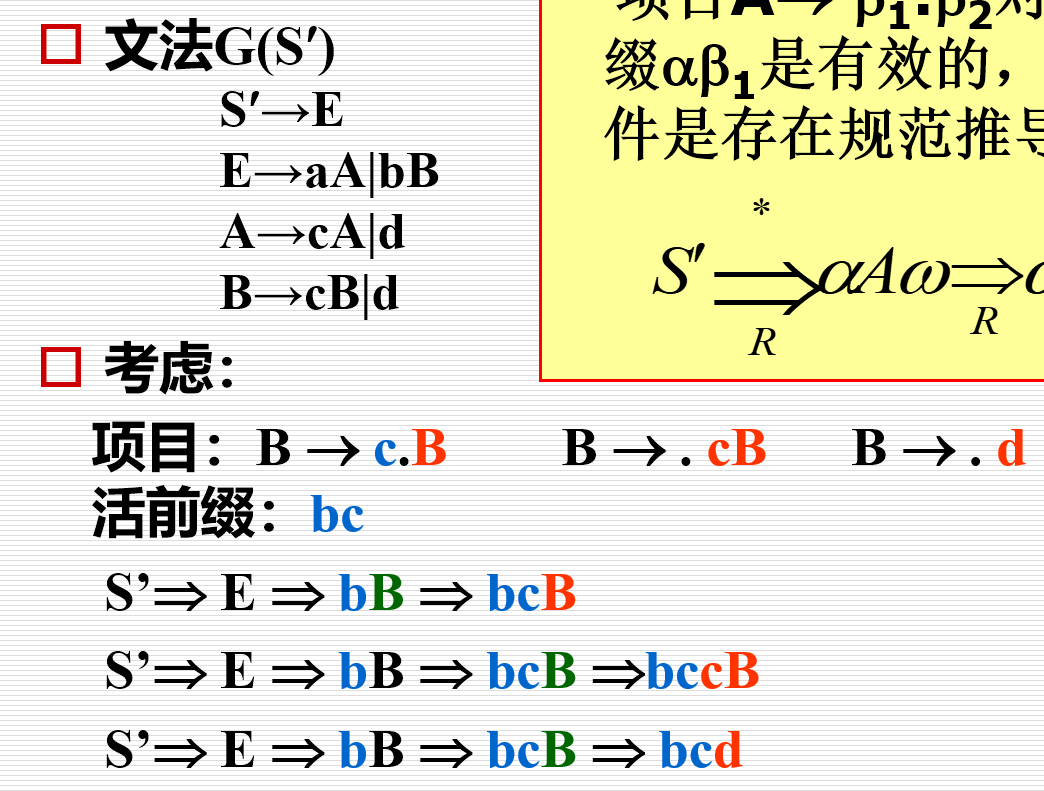
相对较难理解，需要结合上述得到的DFA进行理解 - 有效项目：如果存在规范推导：\(S^\prime\stackrel{*}{\underset{R}{\Rightarrow}}\alpha Aw\underset{R}{\Rightarrow}\alpha\beta_1\beta_2 w\)，则项目\(A\rightarrow \beta_1\cdot\beta_2\)对活前缀\(\alpha\beta_1\)是有效的 - 前一部分已经识别，后一部分正在等待识别 - 在任何时候，分析栈中的活前缀\(X_1X_2\cdots X_m\)的有效项目集正是栈顶状态\(S_m\)所代表的的那个集合 - 也正是从识别活前缀的DFA的初态出发，读出\(X_1X_2\cdots X_m\)所到达的那个项目集合 - 例：如果经过bc，则项目集合5中的3个项目对活前缀都是有效的 - 结论：如果项目\(A\rightarrow\alpha\cdot B\beta\)对活前缀\(\delta\alpha\)是有效的并且\(B\rightarrow\gamma\)是一个产生式，则项目\(B\rightarrow\cdot\gamma\)对该活前缀也是有效的 - 这里的\(\gamma\)指的是某产生式右部 - \(\cdot\)后面出现的串对于活前缀bc都是“有效”的，即此三个项目对于该活前缀是有效的image.png

\(\omega\)是终结符

项目集规范族

  • LR(0)项目集规范族：构成识别一个文法活前缀的DFA的项目集的全体称为文法的LR(0)项目集规范族
  • 拓广文法：
    • 假定文法\(G\)，以\(S\)为开始符号
    • 构造一个\(G^\prime\)，其包含了整个\(G\)，但它引进了一个不出现在\(G\)中的非终结符\(S^\prime\)，并且有一个新的产生式\(S^\prime\rightarrow S\)，其中\(S^\prime\)是\(G^\prime\)的开始符号
    • 则称\(G^\prime\)是\(G\)的拓广文法

闭包

  • 假定\(I\)是文法\(G^\prime\)的任一项目集，定义和构造\(I\)的闭包\(CLOSURE(I)\)如下：
    1. 将\(I\)中的各个项目都添加到\(CLOSURE(I)\)
    2. 若\(A\rightarrow\alpha\cdot B \beta\)属于\(CLOSURE(I)\)，那么对于任何关于\(B\)的产生式\(B\rightarrow\gamma\)，项目\(B\rightarrow\cdot\gamma\)也属于\(CLOSURE(I)\)
    3. 不断重复上述的两个步骤，知道\(CLOSURE(I)\)不在增大为止

      [!note] 直观的讲，\(CLOSURE(I)\)中的项\(A\rightarrow\alpha\cdot B \beta\)表明在语法分析过程的某个点上，我们认为接下来可能会在输入中看到一个能够从\(B\beta\)推导得到的子串。 这个可从\(B\beta\)推导得到的子串的某个前缀可以从\(B\)推导得到，而推导时必然要应用到某个\(B\)的产生式。 因此我们加入了各个\(B\)的产生式对应的项，即对应了上述的第一、二个操作。

GO函数

  • \[GO(I,X) = CLOSURE(J)\]
    • \(GO\)函数是一个状态转换函数
    • \(I\)是项目集
    • \(X\)是文法符号
    • \(J = \{形如A\rightarrow\alpha X\cdot\beta的项目|A\rightarrow\alpha\cdot X\beta\in I\}\)
  • 直观来说，若\(I\)是对某个活前缀\(\gamma\)有效的项目集，那么\(GO(I,X)\)便是对\(\gamma X\)有效的项目集 GO函数的构造.gif
  • GO函数构造的伪代码：image.png
  • 转换函数GO把项目集连接成一个DFA转换图

    [!hint] 至此，我们获得了两种方法来构造DFA 1. 项目->NFA->DFA 2. 利用闭包和GO函数来构造DFA 本质上是一致的，但是书写的形式不一样

  • 构造示例：使用GO函数方法来构造DFA.gif

LR(0)分析表的构造

  • LR(0)文法：
    • 不存在以下情况，则可以称为LR(0)文法：
      • 既含移进项目又含归约项目
      • 含有多个归约项目
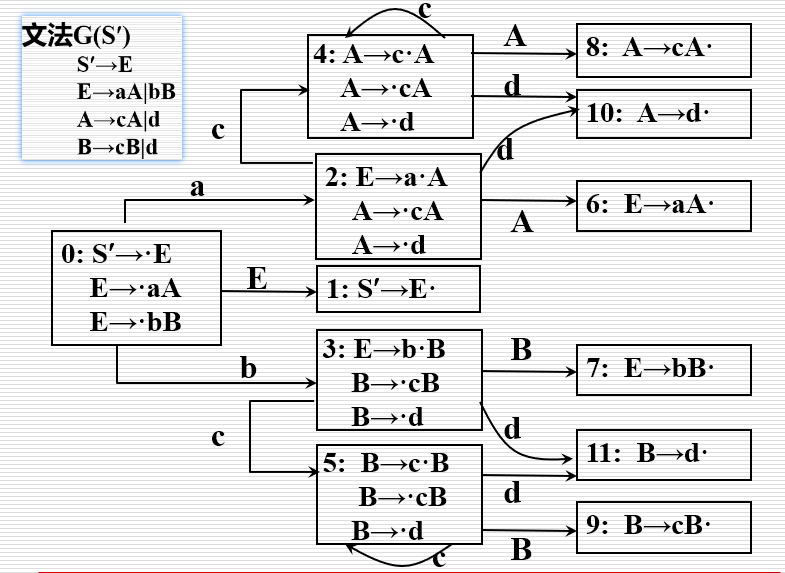
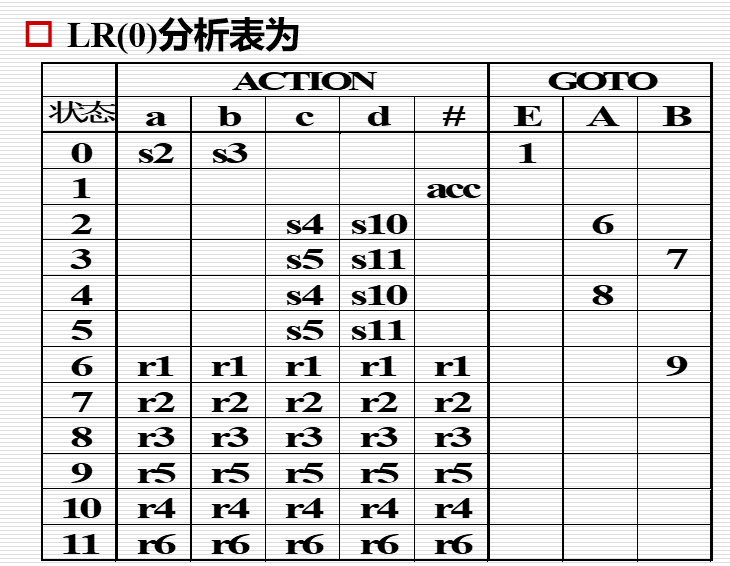
  • 构造LR(0)分析表的算法：
    1. 令每个项目集\(I_k\)的下标\(k\)作为分析器的状态，包含项目\(S^\prime\rightarrow\cdot S\)的集合\(I_k\)的下标\(k\)为分析器的初态
  • 分析表\(ACTION\)和\(GOTO\)子表的构造方法：
    1. 若项目\(A\rightarrow\alpha\cdot a \beta\)属于\(I_k\)并且\(GO(I_k, a)=I_j\)，a为终结符，则令\(ACTION[k,a]=s_j\)
    2. 若项目\(A\rightarrow\alpha\cdot\)属于\(I_k\)，那么，对于任何终结符a（或结束符），令\(ACTION[k, a] = r_j\)
    3. 若项目\(S^\prime\rightarrow S\cdot\)属于\(I_k\)，则令\(ACTION[k, \#]=acc\)
    4. 若\(GO(I_k, A)=I_j\)，A为非终结符，则令\(GOTO[k,A]=j\)
    5. 其余空白格代表“报错” image.png image.png

SLR分析表的构造

LR((0)文法太简单，缺少了实用价值 - SLR方法以LR(0)项和LR(0)自动机为基础 - 即我们根据增广文法\(G^\prime\)构造出\(G^\prime\)的规范项集族C以及GOTO函数 - 需要每个非终结符的\(FOLLOW\)集合 [!attention] SLR分析表 这里只有ACTION和GOTO表的构造与LR(0)不同，项目规范集族的构造是一致的 - 算法：构造一个SLR语法分析表 - 输入：一个增广文法\(G^\prime\) - 输出：\(G^\prime\)的SLR语法分析表函数\(ACTION\)和\(GOTO\) - 方法： 1. 构造\(G^\prime\)的规范\(LR(0)\)项集族\(C=\{I_0, I_1, I_2, \cdots, I_n\}\) 2. 根据\(I_i\)构造得到状态\(i\)： 1. 如果\([A\rightarrow\alpha\cdot a\beta]\)在\(I_i\)中并且\(GO(I_i, a) = I_j\)，\(a\)为一个终结符号，则令\(ACTION[i,a]=s_j\) 2. 如果\(A\rightarrow\alpha\cdot\in I_k\)，那么对于\(FOLLOW(A)\)中的所有\(a\)，则令\(ACTION[i, a]=r_j\) - 这里是与LR(0)不同的地方，在LR(0)中，是对任何终结符a，令\(ACTION[i, a]=r_j\) 3. 如果\(S^\prime=S\cdot\in I_i\)，则令\(ACTION[i,\#]=acc\) - 如果根据上面的规则生成了任何冲突动作，则该文法不是SLR(1)的。此时，无法生成一个语法分析器 3. 如果\(GO(I_i, A)=I_j\)，则\(GOTO[i, A]=j\) - 对于文法：image.png - LR(0)项目集规范族为：image.png - 其中\(I_1, I_2, I_9\)都含有“移进——归约”冲突 - 最终分析表：image.png - #编译原理重点 条件： - 假定LR(0)规范族的一个项目集\(I\)中含有 - \(m\)个移进项目：\(A_1\rightarrow \alpha \cdot a_1\beta_1,A+2\rightarrow \alpha \cdot a_2 \beta_2,\cdots,A_m\rightarrow\alpha\cdot a_m \beta_m\) - \(n\)个归约项目：\(B_1\rightarrow\alpha\cdot, B_2\rightarrow\alpha\cdot,\cdots,B_n\rightarrow\alpha\cdot\) - 那么，如果\(\{a_1,a_2,\cdots,c_m\}\)与\(FOLLOW(B_1)\)、\(FOLLOW(B_2)\)……\(FOLLOW(B_n)\)两两不相交，则隐含在\(I\)中的动作冲突可以通过检查现行输入符号来解决 - 则该文法为SLR(1)文法

规范LR分析表的构造

  • 项目的一般形式：\([A\rightarrow \alpha \cdot \beta, a_1a_2\cdots a_n]\)
    • 向前搜索符串：\(a_1a_2\cdots a_n\)
      • 向前搜索符串仅对于归约项目\([A\rightarrow \alpha \cdots, a_1a_2\cdots a_n]\)有意义
        • 意味着：当它所属的状态呈现在栈顶且后续的k个输入符号为\(a_1a_2\cdots a_n\)时，才执行归约动作
      • 对于其他的移进或待归约项目，无用
  • 项目集\(I\)的闭包\(CLOSURE(I)\)的构造方法：
    • \(I\)的任何项目都属于\(CLOSURE(I)\)
    • 若项目\([A\rightarrow \alpha \cdot B\beta,a]\)属于\(CLOSURE(I)\)，并且\(B\in \xi\)是一个产生式，那么，对于\(b\in FIRST(\beta a)\)，如果\([B\rightarrow \cdots \xi, b]\)原来不在\(CLOSURE(I)\)中，则将其添加进去
    • 重复执行上一个步骤，直到\(CLOSURE(I)\)不再增大

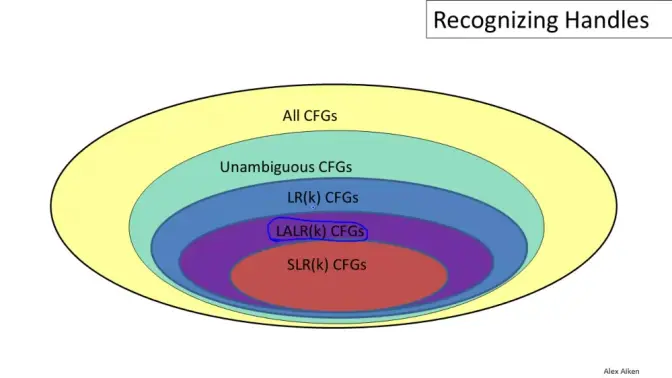
  • 编译原理重点 LR分析的包含关系：\(LR(0)\subset SLR(1)\subset LR(1)\subset 无二义文法\)

    image.png