浮点数
浮点表示对形如\(V=x\times 2^y\)的有理数进行编码
二进制小数
\(\(d= \sum _{i=-n}^{m}10^{i}\times d_{i}\)\) - 与二进制整数的计算方式相同 - 整数部分:小数点左边的数字的权是10的正幂次 - 小数部分:小数点右边的数字的权是10的负幂次 - 对于这种表示方法,增加二进制表示的长度可以提高表示的精度
IEEE浮点表示
\(\(V=(-1)^s\times M \times 2^E\)\)
- 一个浮点数的组成与其编码方式: - 符号(Sign):\(s\)决定数的正负
- 1位符号位
- 尾数(Significand):\(M\)是一个二进制小数,其范围是\(1\sim 2-\varepsilon\)或\(0\sim 1-\varepsilon\)
- \(n\)位小数字段编码\(M\):\(frac=f_{n-1}\cdots f_{1}f_{0}\)
- 阶码(Exponent):\(E\)的作用是对浮点数加权,其权重是\(e\)的\(E\)次幂
- \(k\)位阶码字段编码\(E\):\(exp=e_{k-1}\cdots e_{1}e_{0}\)
- 根据\(exp\)的值,被编码的值可以分为三种不同的情况
1. 规格化的值:
- 符号(Sign):\(s\)决定数的正负
- 1位符号位
- 尾数(Significand):\(M\)是一个二进制小数,其范围是\(1\sim 2-\varepsilon\)或\(0\sim 1-\varepsilon\)
- \(n\)位小数字段编码\(M\):\(frac=f_{n-1}\cdots f_{1}f_{0}\)
- 阶码(Exponent):\(E\)的作用是对浮点数加权,其权重是\(e\)的\(E\)次幂
- \(k\)位阶码字段编码\(E\):\(exp=e_{k-1}\cdots e_{1}e_{0}\)
- 根据\(exp\)的值,被编码的值可以分为三种不同的情况
1. 规格化的值: - 最普遍的情况:\(exp\)不全为\(1\)或\(0\)
- 阶码的值\(E=e-Bias\)
- 此时阶码字段被解释为以偏置形式表示的有符号整数
- \(Bias=2^{k-1}-1\)
- 单精度的情况下为127
- 双精度的情况下为1023
- 尾数的值\(M=1+f=1.f_{n-1}...f_1f_0\)
- 小数字段\(frac\)被解释为描述小数值\(f=0.f_{n-1}...f_1f_0\)
- 这种方式也被称为隐含的以1开头表示
2. 非规格化的值
- 最普遍的情况:\(exp\)不全为\(1\)或\(0\)
- 阶码的值\(E=e-Bias\)
- 此时阶码字段被解释为以偏置形式表示的有符号整数
- \(Bias=2^{k-1}-1\)
- 单精度的情况下为127
- 双精度的情况下为1023
- 尾数的值\(M=1+f=1.f_{n-1}...f_1f_0\)
- 小数字段\(frac\)被解释为描述小数值\(f=0.f_{n-1}...f_1f_0\)
- 这种方式也被称为隐含的以1开头表示
2. 非规格化的值 - 阶码域全部为0
- 阶码值:\(E=1-Bias\)
- 这样偏置值的设置可以使非规格化值平滑的转换到规格化值
- 尾数值:\(M=f\)
- 用途:
- 提供了一种表示数值0的方法
- 因为在规格化表示中,有\(M\ge 1\)
- 根据符号位的不同,有\(-0\)与\(+0\)
- 方便的表示接近于0的数
3. 特殊值:
- 阶码域全部为0
- 阶码值:\(E=1-Bias\)
- 这样偏置值的设置可以使非规格化值平滑的转换到规格化值
- 尾数值:\(M=f\)
- 用途:
- 提供了一种表示数值0的方法
- 因为在规格化表示中,有\(M\ge 1\)
- 根据符号位的不同,有\(-0\)与\(+0\)
- 方便的表示接近于0的数
3. 特殊值:

[!具体分类] - 规格化的:
- 非规格化的:
- 无穷大:
- NaN(Not a Number):
数字示例
- 一个6位格式:\(k=3\quad n=2\)

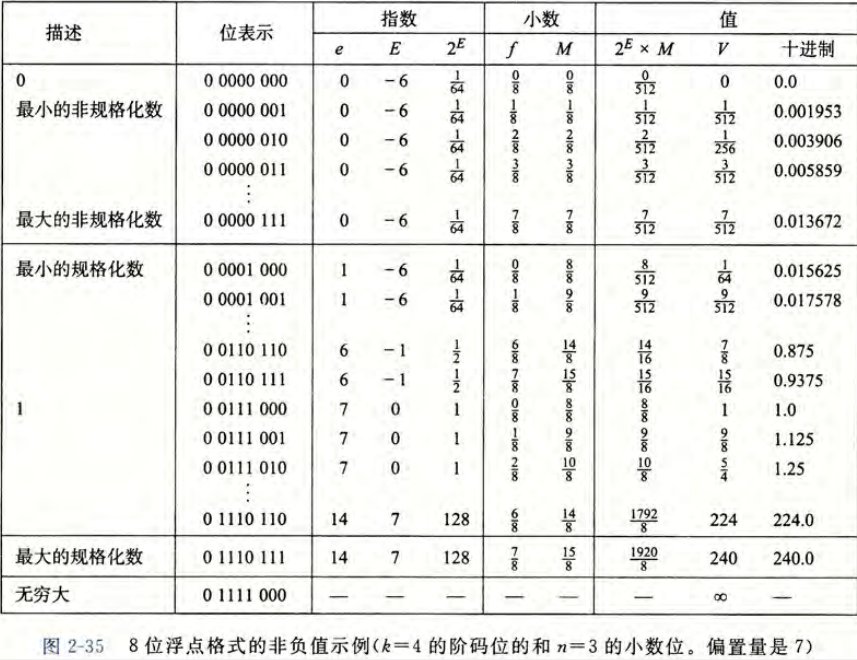
- 一个8位浮点数的表示:\(k=4\quad n = 3\)
舍入
 - 向偶数舍入的方式:将数字向上或向下舍入,使结果的最低有效数字是偶数
- 向偶数舍入的方式:将数字向上或向下舍入,使结果的最低有效数字是偶数
[!向偶数舍入] 在计算一组数的平均值时,使用向上或向下舍入的方式,会使计算一组数的平均值偏高或偏低,向偶数舍入在大多数现实情况中避免了这一统计偏差,因为向上舍入与向下舍入的概率各位50%,在计算平均值时候的影响相对较小
浮点运算
- 由于溢出的存在,在一定情况下,不满足结合律
- \((3.14+1e10)-1e10=0\)
- \(3.14+(1e10-1e10)=3.14\)