跳转至

TranSG

The Proposed Approach

  • 使用 3 D骨架序列: \(X=(x_1, \cdots, x_f)\) 表示一个身份 y, 其中
    • \(x_t\)使用 \(J\) 个身体关节的 3 D 坐标点表示第 \(t^{th}\) 个骨架
    • \(y\in \{1, \cdots, C\}\), \(C\) 是总的人数 (类别数)
  • 训练集,查询集 (probe set)和参考集 (gallery set)
    • 训练集: \(\Phi_T=\left\{\boldsymbol{X}_i^T\right\}_{i=1}^{N_1}\), 包括了 \(N_1\) 组不同人物骨骼序列
    • 查询集: \(\Phi_P=\left\{\boldsymbol{X}_i^P\right\}_{i=1}^{N_2}\), 包括了 \(N_2\) 组不同人物骨骼序列
    • 参考集: \(\Phi_G=\left\{\boldsymbol{X}_i^G\right\}_{i=1}^{N_3}\), 包括了 \(N_3\) 组不同人物骨骼序列

      [!note] probe set 与 gallery set - probe set: probe 的原意是探针, 附带有查询的意思, 则 probe set 也可以理解为query set, 也就是说, 在测试时候是通过从 probe set 中选取元素以到gallery set 中寻找, 最终的测试阶段对模型性能的评估是根据 probe 中元素查询的效果来反映的 - gallery set: gallery 的意思是画廊, 类似于在一个人脸识别系统中, 每个人都在这个人脸识别系统中注册了自己的脸部图像, 并且与自己的身份相绑定, 形成一个巨大的数据库, 就如同画廊一般展示出来.

  • 目的: 学习一个能够将骨骼序列映射到一个有效表示的编码器
    • encoded skeleton sequence representations in the probe set(查询集合中编码过的骨骼序列表示) -> representations of the same identity in the gallery set(参考集中对应身份)
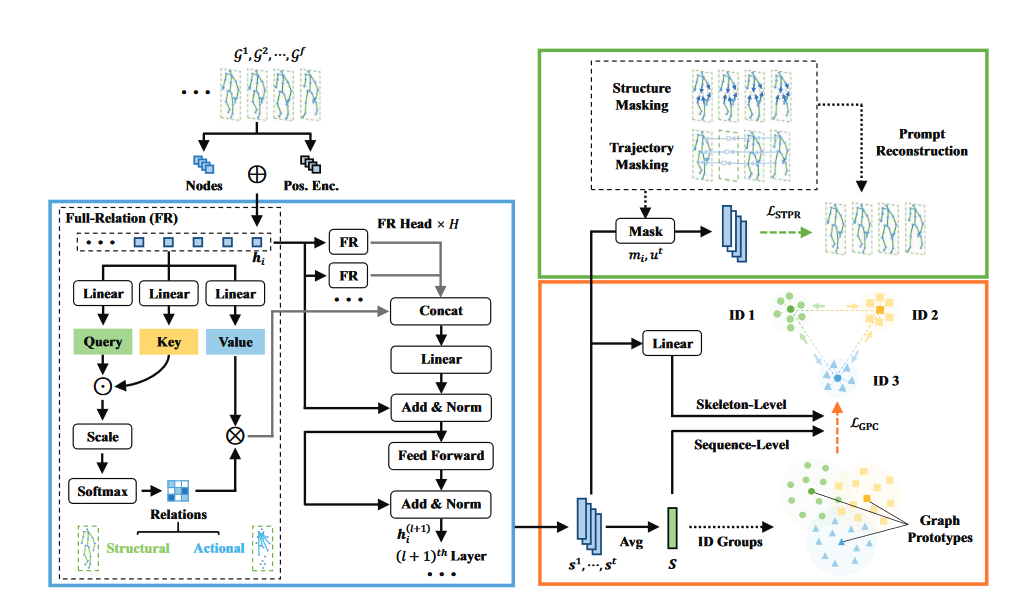
  • overview of network: image.png
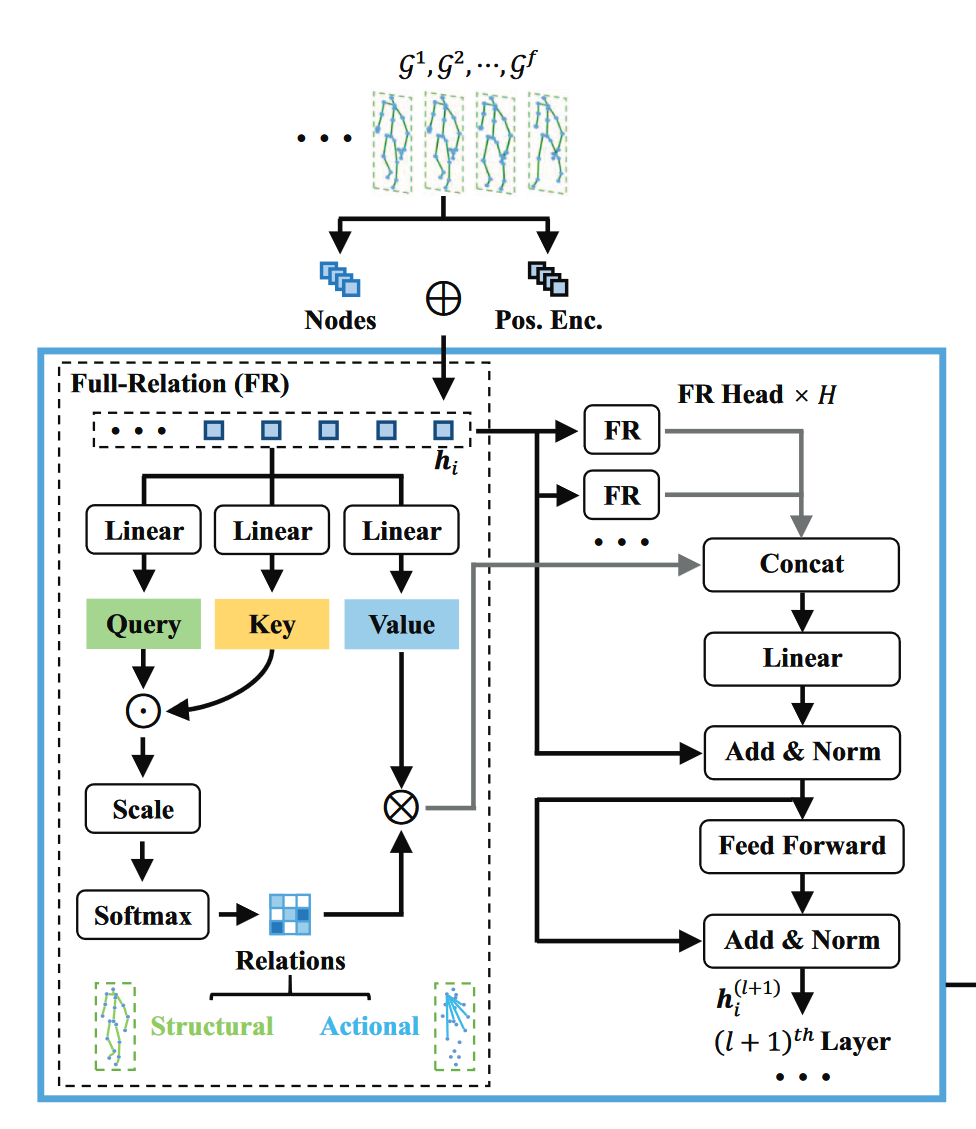
    1. 将骨架图像 \(G_1, G_2, G_3, \cdots\) 导入到 SGT (skeleton graph transformer)中, 获得身体结构之间的关系 image.png
      • 在网络中部署了多个 SGT 层
      • 第 \(l^{th}\) 层的输出 \(h_i^{(l + 1)}\) 作为第 \((l+1)^{th}\) 层的输入
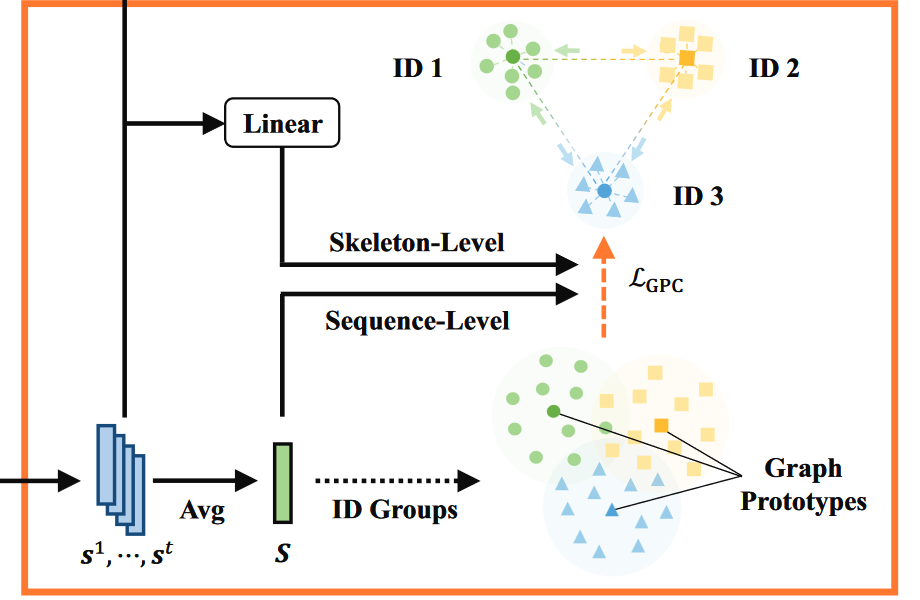
    2. 利用属于不同身份（ID）的图形特征的中心点生成图形原型 image.png
      • 通过 \(\mathcal{L}_{GPC}\) 增强同一个类型的相似性 (距离), 减小不同类型之间的相似性 (距离)
    3. 随机屏蔽骨架图和结点轨迹, 将相应的掩蔽图作为上下文, 通过最小化 \(\mathcal{L}_{STPR}\) 来促进重建
    4. 将从以上方法中学到的骨架图表示, 用于人员重识别 (ReID)

Skeleton Graph Construction

  • 以身体关节为结点, 以相邻关节之间的连接结构来构建骨架图
  • 骨架图 \(\mathcal{G}^t\)
    • 以身体关节为结点\(\mathcal{V}^t=\{ v _ { 1 } ^ { t } , v _ { 2 } ^ { t } , \cdots , v _ { j } ^ { t }\} , v _ { i } ^ { t } \in \mathbb{R} ^ { 3 } , i \in \left\{ 1 , \cdots , J \right\}\)
    • 以相邻关节之间的连接结构为边\(\mathcal{E}^t = \left\{ e _ { i , j } ^ { t } | v _ { i } ^ { t } , v _ { j } ^ { t } \in \mathcal{V} ^ { t } \right\} , e _ { i , j } ^ { t } \in \mathbb{R}\)
  • 骨架图 \(\mathcal{G}^t\) 的邻接矩阵 \(A^t\in\mathbb{R}^{J\times J}\) 表示 \(J\) 个结点之间的关系

Skeleton Graph Transformer

  • 人类骨架的两个特点:
    1. 身体结构特征: 可以从相邻身体关节之间的关系推断出来
    2. 骨架动作模式: 以不同身体不为之间的关系为特征
  • 对于图结点, 首先利用预定义的图结构来获得图结点的位置编码: (\(\Delta = I - D ^ { - 1 / 2 } A D ^ { - 1 / 2 } = U ^ { T } \Lambda U\)\)
    • \(A, D\): 邻接矩阵和度矩阵
    • \(\Lambda,U\): 拉普拉斯特征值和特征向量
    • \(U ^ { T } \Lambda U\) 是拉普拉斯矩阵的因子

      [!note] \(A\) 由于统一数据集中的 \(A^t\) 共享相同的初始化邻接矩阵, 所以使用 \(A\) 来表示 \(A^t\)

  • 通过学习得到的位置编码
    • 首先, 对于结点 \(v_i\), 采用K 个最小的非平凡特征向量作为结点的位置编码, 表示为 \(\lambda_i\in \mathbb{R}^K\)
    • 接下来, 通过仿射变换将它们映射到相同维度 d 的特征空间 (\(\boldsymbol{h}_i=\left(\mathbf{W}_v \boldsymbol{v}_i+\boldsymbol{b}_v\right)+\left(\mathbf{W}_p \boldsymbol{\lambda}_i+\boldsymbol{b}_p\right)\)\)
      • \(h_i \in \mathbb{R}^d\) 表示 \(i^{th}\) 个位置编码结点表示
      • \(\mathbf{W}_v \in \mathbb{R}^{d \times 3}, \mathbf{W}_p \in \mathbb{R}^{d \times K}, \boldsymbol{b}_v, \boldsymbol{b}_p \in \mathbb{R}^d\) 是节点 \(v_i\) 及其对应位置编码的特征变换的可学习参数

[!note] 位置编码 Positional Encoding 为了使用序列的顺序信息, 通过在输入表示中添加位置编码来注入绝对的或相对的位置信息. 位置编码可以通过学习得到也可以直接固定得到. 在本项目中添加位置信息的好处: 结构上邻近的节点具有相似的位置特征，而较远的节点则具有更多不同的位置特征，从而鼓励更有效的节点表征学习

[!note] 为什么会有两个位置编码? 因为在这个过程中，节点 vi 的特征和其对应的位置编码都被视为位置编码。节点 \(v_i\) 的特征是通过学习得到的，而其对应的位置编码 \(\lambda_i\) 是通过图的拉普拉斯矩阵计算得到的。这两个位置编码在最后被相加，共同构成了节点的位置编码表示。

  • 通过使用多个独立的全连接头捕捉身体关节之间的固有关系, 并且通过整合相关的特征更新原来的结点表示: (\(\boldsymbol{w}_{i, j}^{k, l}=\operatorname{Softmax}_j\left(\frac{\left(\boldsymbol{Q}^{k, l} \boldsymbol{h}_i^{(l)}\right) \cdot\left(\boldsymbol{K}^{k, l} \boldsymbol{h}_j^{(l)}\right)}{\sqrt{d_{\mathrm{k}}}}\right)\)\)(\(\hat{\boldsymbol{h}}_i^{(l)}=\boldsymbol{O}^l \|_{k=1}^H\left(\sum_{j \in \mathcal{N}_i} \boldsymbol{w}_{i, j}^{k, l} \boldsymbol{V}^{k, l} \boldsymbol{h}_j^{(l)}\right)\)\)
    • \(\boldsymbol{Q}^{k, l}, \boldsymbol{K}^{k, l}, \boldsymbol{V}^{k, l} \in \mathbb{R}^{d_{\mathrm{k}} \times d}\): 第 \(l^{th}\) 层 SGT 层中的第 \(k^{th}\) 层 FR 头的 query, key, value 变换的参数矩阵
    • \(\sqrt{d_{\mathrm{k}}}\): 缩放比
    • \(\boldsymbol{w}_{i, j}^{k, l}\): 第 \(l^{th}\) 层中的第 \(k^{th}\) FR 头获得的结点 \(i\) 与结点 \(j\) 之前的关系值(归一化后)
    • \(\|\): 连接符
    • \(H\): FR 头的数量
    • \(\hat{\boldsymbol{h}}_i^{(l)}\): 第 \(l\) 层中不同结点 \(i\) 的结点特征

      [!note] SGT 很自然的将自注意力机制推广到图结点的全关系学习, 可以被视为一种可同时捕捉相邻和非相邻身体组成结点的结构和行为关系的一种通用范式.

  • 多个 FR 头使模型能够共同处理来自不同特征子空间结点关系, 并将更多关键关联结点特征整合到最终的结点表示中
  • 应用一个 FFN (Feed Dorward Network)获得SGT 层的中间结点表示和输出结点表示:
    • 中间节点表示: \(\(\overline{\boldsymbol{h}}_i^{(l)}=\operatorname{Norm}\left(\boldsymbol{h}_i^{(l)}+\hat{\boldsymbol{h}}_i^{(l)}\right)\)\)
    • 输出结点表示: (\(\boldsymbol{h}_i^{(l+1)}=\operatorname{Norm}\left(\overline{\boldsymbol{h}}_i^{(l)}+\mathbf{W}_2^l \sigma\left(\mathbf{W}_1^l \overline{\boldsymbol{h}}_i^{(l)}\right)\right)\)\)
      • \(\mathbf{W}_1^l \in \mathbb{R}^{2 d \times d}, \mathbf{W}_2^l \in \mathbb{R}^{d \times 2 d}\)是 FFN 的可学习参数
      • \(\sigma\)表示 ReLU 激活函数
  • 将每个骨架图中的特征平均化 (average), 作为相应的图表示, 然后将\(f\)个连续的图表示通过以下的公式整合到一起, 获得一个最终的序列级图表示 (the final sequence-level graph representation \(S\): (\(\boldsymbol{S}=\frac{1}{f} \sum_{t=1}^f \boldsymbol{s}^t=\frac{1}{f} \sum_{t=1}^f \frac{1}{J} \sum_{i=1}^J \boldsymbol{h}_i^t\)\)
    • \(S, s^t\in \mathbb{R}^d\)分别为序列级和骨架级的图表示，分别对应序列中的一个骨架序列\(X\)和第\(t\)个骨架\(x_t\)
  • 为了简要的表述, 使用\(h^t_i\)表示编码后的第\(t\)个骨架图中的第\(i\)个结点的表示
    • 这里假设每个具有聚集关系特征的结点表示对图表示的贡献是相等的, 并且每个骨架图在表示个体的模式时具有相同的重要性

Graph Prototype Constrastive Learning

[!abstract] 即使每个人都有自己特别的步态, 但每个人的骨骼也会有一些共同的特征. 在这一部分, 就是为了找出最具代表性的骨架特征 (称为原型 prototype), 来学习一个区分模式. 最直接的方法是对序列表征进行聚类, 以挖掘原型, 但是这样的方法只能生成不确定较大或不可靠的身份识别原型, 例如, 当存在较大的类内变异时, 两个具有不同模式的同类序列可能会被聚类到两个原型组中. 为了使模型能够更加可靠的生成表示图的特征, 我们提出利用图的特征中心点作为图的原型, 并且与序列级和骨架级图特征进行对比, 以学习用于 ReID 的鉴别表征. - 给定已编码过的训练骨架序列\(\{X^T_i\}^{N_1}_{i=1}\)图表示\(\{S^T_i\}^{N_1}_{i=1}\), 我们将其分组为\(\{\hat{\mathbb{S}}_k\}^C_{k=1}\) - \(\hat{\mathbb{S}}_k=\{S_{k, j}\}^{n_k}_{j=1}\)表示属于第\(k\)个身份的图表示集合 - \(S_{k, j}\)为第\(j\)个序列级图表示，\(n_k\)表示\(k\)类序列的个数 - 则根据上述的描述, 我们就可以获得一个原型: \(\(c_k=\frac{1}{n_k}\sum^{n_k}_{j=1}S_{k, j}\)\) - \(c_k\): 第\(k\)个身份的原型 - 为了局将与每个身份的代表性图原型, 以便从附加和序列两个层面学习与身份相关的辨别语义, 我们提出图原型对比 (GPC, graph prototype constrastive)损失法:\(\(\mathcal{L}_{GPC}=\alpha\mathcal{L}^{seq}_{GPC}+(1-\alpha)\mathcal{L}^{ske}_{GPC}\)\) - \(\alpha\)为融合权重系数 - \(\(\begin{gathered} \mathcal{L}_{\mathrm{GPC}}^{s e q}=\frac{1}{N_1} \sum_{k=1}^C \sum_{j=1}^{n_k}-\log \frac{\exp \left (\boldsymbol{S}_{k, j} \cdot \boldsymbol{c}_k / \tau_1\right)}{\sum_{m=1}^C \exp \left (\boldsymbol{S}_{k, j} \cdot \boldsymbol{c}_m / \tau_1\right)}, \\ \mathcal{L}_{\mathrm{GPC}}^{s k e}=\frac{1}{f N_1} \sum_{k=1}^C \sum_{j=1}^{n_k} \sum_{t=1}^f-\log \frac{\exp \left (\mathcal{F}_1\left (s_{k, j}^t\right) \cdot \mathcal{F}_2\left (\boldsymbol{c}_k\right) / \tau_2\right)}{\sum_{m=1}^C \exp \left (\mathcal{F}_1\left (s_{k, j}^t\right) \cdot \mathcal{F}_2\left (\boldsymbol{c}_m\right) / \tau_2\right)} . \end{gathered}\)\) - \(c_m\)表示\(m-class\)的图原型 - \(s^{t}_{k, j}\)表示序列中第\(t\)个骨架的图形表示, 对应于属于第\(k\)个特征的 \(S_{k, j}\), \(τ1, τ2\) 是对比学习的温度 - \(\mathcal{F}1 ( · ), \mathcal{F}2 ( · )\)为线性投影头，用于将骨架级图表示和图原型变换到同一对比空间\(\mathbb{R}_d\)中 [!attention] 图原型是由更高层次的表征生成的, 从\(\mathcal{L}^{ske}_{GPC}\)中的可学习线性投影可以看作是将两个层次的相关图特征整合在一起进行对比学习。所提出的 GPC 损失本质上是一种广义骨架原型对比损失，它结合了[[TranSG#Skeleton Graph Transformer|联合级关系编码]]（见第 3.2 节）、骨架级和序列级图形学习 (见\(\mathcal{L}_{GPC}\))

Graph Structure-Trajectory Prompted Reconstruction Mechanism

  • 两个基于图上下文的提示词重构图结构和动态:
    • 同一图的部分结点位置
    • 连续图之间的部分结点轨迹

Graph Sturcture Prompted Reconstruction

  • 给定经由 SGT 编码的具有\(J\)个编码结点的第\(t\)个骨架图表示, 首先随机屏蔽结点位置, 生成屏蔽图 (mask)表示: (\(\hat{s}^t = \frac{1}{J-a}\sum^J_{i=1}m_ih^t_i\)\)
    • \(a\): 掩码的数量
    • \(m_i\): 应用于第\(i\)个结点的表示\(h^t_i\)上的二进制掩码值
    • \(J-a=\sum^J_{i=1}m_i\)
  • 骨架重建: 利用每个结点的空间位置信息和关系特征, 结合屏蔽图表示, 进行骨架重建(\(\hat{x}^t = f_s (\hat{s}^t)\)\)
    • \(f (\cdot)\): 一个带有一个隐藏层的 MLP 网络，用于结构提示的骨架重建
    • \(\hat{x}^t\in\mathbb{R}^{J\times 3}\): 预测结果

      [!attention] \(\hat{x}^t = f_s (\hat{s}^t)\)不仅利用未被掩盖的节点表示来重建它们的位置，而且利用它们作为上下文来预测被掩盖的节点位置。

Graph Trajectory Prompted Reconstruction

  • 为了让模型从骨架图中捕获更多独特的时间模式, 我们提出基于图轨迹的部分动力学来重建图轨迹
    • 我们对每个节点的轨迹进行随机屏蔽: (\(T_i=\frac{1}{f-b}\sum^f_{t=1}u^th^t_i\)\)
      • \(T_i\in \mathbb{R}^d\): \(i\)节点轨迹 (即\(h_i^1 , \cdots , h^f_i\))的掩码表示
      • \(b\): 轨迹掩码的个数
      • \(U_t\): 应用于第\(i\)个节点轨迹中第\(t\)个位置的二进制掩码值
      • \(\sum^f_{t=1}u^t=f-b\)
  • 掩模轨迹表示\(T_i\)保留了不同身体节点的部分图动态，进而用于提示骨架重构:(\(\overline { x } _ { i } = f _ { t } ( T _ { i } )\)\)
    • \(\overline { x } _ { i } \in \mathbb{R} ^ { f \times 3}\): 表示具有一个隐藏层的 MLP 网络\(f_t ( · )\)预测的第\(i\)个人体关节点的时间轨迹
  • 优点: 便于捕获关键时间动态和语义, 从而推断轨迹上遗漏的结点位置
  • 通过转置原始预测位置矩阵\((\overline{x}_1,\cdots, \overline{x}_J)\in\mathbb{R}^{J\times f\times 3}\), 将预测的第\(i\)个训练序列表示为\(\overline{X}_i\in\mathbb{R}^{J\times f\times 3}\)

Combine

  • 结合图结构和轨迹提示重建 STPR 目标: (\(\mathcal{L} _ { S T P R } = \beta \mathcal{L} _ { S T P R } ^ { s t } + ( 1 - \beta ) \mathcal{L} _ { S T P R } ^ { t r }\)\)
    • 其中(\(\begin{aligned} & \mathcal{L}_{\mathrm{STPR}}^{s t}=\frac{1}{N_1} \sum_{i=1}^{N_1}\left\|\hat{\boldsymbol{X}}_i-\boldsymbol{X}_i^T\right\|_1, \\ & \mathcal{L}_{\mathrm{STPR}}^{t r}=\frac{1}{N_1} \sum_{i=1}^{N_1}\left\|\overline{\boldsymbol{X}}_i-\boldsymbol{X}_i^T\right\|_1 . \end{aligned}\)\)
      • \(\beta\): 融合因子
      • \(X_i^T∈R^{f × J × 3}\)表示第\(i\)个训练骨架序列的真实位置，\(‖·‖_1\)表示\(\ell_1\)范数

        [!note] \(\ell_1\) 使用\(\ell_1\)重建损失, 因为他可以缓解大损失的梯度爆炸, 同时为小损失的位置提供足够的梯度, 以促进更精确的重建.

The Entire Approach

Experiments

参考