Sequential Logic Design
Timing of Sequential Logic
当时钟上升的时候, 输入是稳定的 (0/1), 则该模块是明确定义的, 但若此时输入在时钟上升时, 是同时变化的, 会发生什么?
类比: 正在使用相机拍摄一只青蛙, 在青蛙跳跃前后, 待青蛙的状态稳定下来后所拍摄到的照片是清晰的, 而若在按下快门时候, 青蛙同时跃起, 则拍摄到的青蛙很可能就是模糊的. 在摄影中, 这称为快门时间, 若物体在快门时间内是静止的, 则可以拍摄到清晰的物体, 若物体在快门时间内移动, 则会出现模糊.
在时序元件中也是如此, 在时钟边沿也有这么一个"快门时间", 我们必须保证在这个"快门时间"中, 输入是稳定的状态, 此前的这段时间称为建立时间 (setup time), 之后称为保持时间 (hold time), 在建立时间和保持时间中, 输入的数据必须是稳定的才能产生稳定的输出, 除此两个时间之外, 输入可以随意的变动.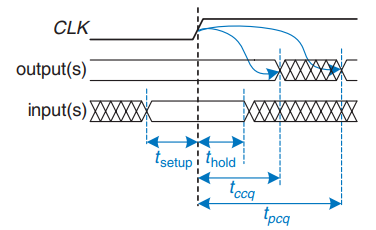 
这就意味着, 时钟周期必须足够长, 才能使得所有的信号稳定下来, 这也限制了系统的运行速度. 在真实的系统中, 时钟到达不同的触发器的时间是不一致的, 这个变量称为时钟偏移 (clock skew). 这段时间的存在又进一步增加了时钟周期的长度.
The Dynamic Discipline
对于一个同步时序电路, 当时钟上升时候, 输出在 \(t_{ccq}\) (clock-to-Q contamination delay) 后开始改变, 并且输出在 \(t_{pcq}\) (clock-to-Q propagation delay)后稳定下来.
\(t_{ccq}\) 和 \(t_{pcq}\) 分别代表了电路中最快和最慢的延迟. 对于一个电路来说, 如果想要采样到正确的数据, 其输入在上升沿之前必须已经稳定 \(t_{setup}\) 时间, 并且在上升沿之后继续保持稳定 \(t_{hold}\) 时间, 这两个时间之和就称为孔径(快门)时间 (aperture time).
简单理解: 如果我们时钟上升沿的地方视作 0, 那么输入不能改变的范围就是 [-setup time, hold time].
The Dynamic Discipline 就是指出了同步时序电路中的输入必须在 setup 和 hold 期间保持稳定. 通过执行这一要求, 我们就可以保证触发器可以在输入不改变时候进行采样, 这样就可以将信号看做是离散的了.
System Timing
时钟周期 \(T_c\) 指的是两个时钟上升沿之间的时间, 其倒数 \(f_c\) 就是时钟频率.
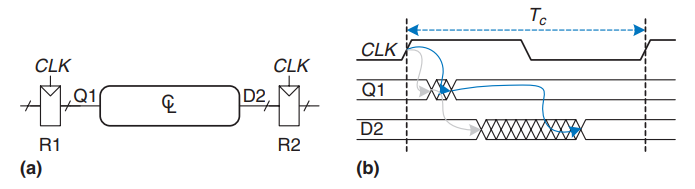对于上图, 在时钟上升沿时候, \(R1\) 在一定时间后产生输出 \(Q1\), \(Q1\) 进入组合逻辑块, 产生 \(R2\) 的输入信号 \(D2\). 在右侧的时序图中, 灰色箭头表示 \(R1\) 和组合逻辑的 contaminaion delay, 蓝色箭头表示 \(R1\) 和组合逻辑的 propagation delay. 接下来对上图的情况进行分析.
Setup TIme Constraint
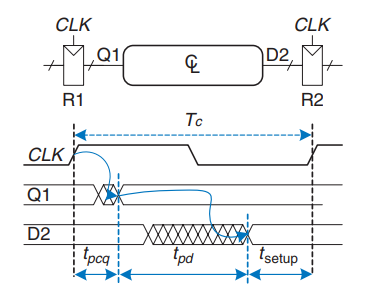图中的路径表示了最大的延迟, 为了满足 \(R2\) 的 setup time, \(D2\) 必须在下一个上升沿的 \(t_{setup}\) 前稳定下来. 因此, 根据时序图, 有:$$
T_c\ge t_{pcq} + t_{pd} + t_{setup}
$$
其中, 个人设计师能够控制的是 \(t_{pd}\), 即信号在组合逻辑中的传递时间, 对上述的公式进行变式, 可以得到:$$
t_{pd} \le T_c - (t_{pcq}+t_{setup})
$$
\(t_{pcq}+t_{setup}\) 被称为时序开销 (sequencing overhead): 理论上, 整个 \(T_c\) 应该都用于组合逻辑所消耗的时间 \(t_{pd}\), 但现实情况是时序的传播也是需要时间的. 上一个不等式就被称为建立延迟限制 (setup time constraint)或最大延迟限制 (max-delay constraint)
如果组合逻辑的传播延迟过长, 则 \(R2\) 的输入在时钟上升沿时候无法稳定下来, 导致 \(R2\) 采样到一个错误的结果甚至是非法的逻辑, 此时电路会发生故障.
这个问题可以通过延长时钟周期或优化设计以获得更短的传播延迟来解决.
Hold Time Constraint
对于寄存器 \(R2\), 其输入的 \(D2\) 在上升沿后的一定时间内不能改变, 这段时间称为 \(t_{hold}\)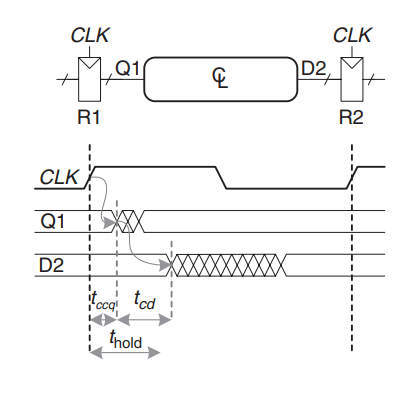 
根据对上图的分析, 输入 \(D2\) 在上升沿后的 \(t_{ccq}+t_{cd}\) 后立即改变, 因此我们可以得到对于 \(t_{hold}\) 的限制条件为: $$
t_{ccq} + t_{cd} \ge t_{hold}
$$
进行简单的转换后, 就可以得到所谓的保持时间限制/最小延迟限制, 用来限制通过组合逻辑的最小延迟: $$
t_{cd} \ge t_{hold} - t_{ccq}
$$
还有一种情况是, 两个触发器直接相联, 中间没有其他的组合逻辑, 此时的 \(t_{cd} = 0\)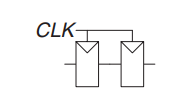 
此时就可以得到 \(t_{hold} \le t_{ccq}\).
然而, 保持时间限制是非常重要的, 如果违背了这一点, 唯一的解决方法就是提高 contamination delay, 这就需要重新设计电路, 重新设计电路的成本是非常高的, 不像建立时间限制那样可以通过调整时钟周期来解决.
Putting It All Together
时序逻辑电路的建立时间和保持时间决定了触发器之间的组合逻辑的最大和最小延迟. 现代的触发器都会将其设计为能够满足其间的组合逻辑的延迟为 0 的情况, 使得两个触发器可以直接相联. 而最大延迟则限制了关键路径上的逻辑门数量.
Clock Skew
时钟到达不同寄存器的时间有所区别, 称为时钟偏移.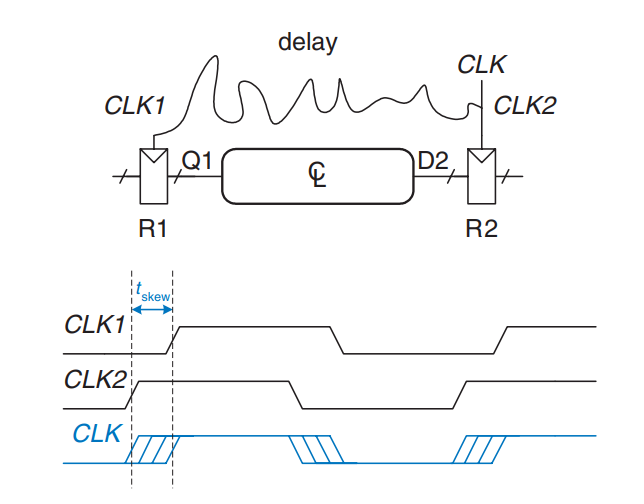 
导致这个问题的原因有: 1. 连线到不同寄存器的长度不一致; 2. 噪声的影响; 3. 部分是门控时钟, 而部分不是.
在进行时序分析的时候, 我们会考虑最糟糕的情况, 这样才能保证电路能够在任何环境下都正常工作.